Lyhennetty oktaedri — arkimedealainen kappale, 8 kuusikulmiota ja 6 neliötä
Lyhennetty oktaedri on arkimedealainen kappale, joka tunnetaan myös englanniksi nimellä "truncated octahedron". Sillä on yhteensä 14 pintaa: 8 on kuusikulmioita ja 6 neliöitä. Lyhennetty oktaedri muodostuu leikkaamalla (trunkoimalla) oktaedrin kärjet; oktaedrin jokaisessa kärjessä kohtaa neljä särmää, joten kärkien leikkaaminen korvautuu neliöillä ja alkuperäiset kolmionmuotoiset sivut muuttuvat kuusikulmioiksi.
Perusominaisuudet
- Pintojen lukumäärä (F): 14 (8 kuusikulmiota + 6 neliötä)
- Särmien lukumäärä (E): 36
- Huippujen lukumäärä (V): 24
- Huippujen kokoonpano: jokaisessa huipussa liittyy yksi neliö ja kaksi kuusikulmiota — merkitty usein konfiguraatiolla 4.6.6
- Symmetria: oktaedrin symmetrian jatke, eli täydellinen oktaedrisessa luokassa oleva symmetriarakenne (korkea symmetria, sama kuin oktaedrilla/kubilla)
- Schläfli- tai truncaatiosymboli: t{3,4} (trunkkaus oktaedrista)
- Erityisominaisuus: lyhennetty oktaedri on yksi harvoista arkimedealaisista kappaleista, joka täyttää avaruuden säännöllisenä tilajaotuksena (se voidaan sovittaa täyteen avaruutta ilman rakoja — ns. space-filling polyhedron)
Muoto ja rakentuminen
Arkimedealainen muunnos saadaan leikkaamalla oktaedrin kärjet sopivalla syvyydellä niin, että jäljelle jäävät kuusikulmiot ja syntyvät neliöt ovat säännöllisiä. Tällöin alkuperäiset kolmionmuotoiset kasvot laajenevat kuusikulmioiksi ja kärkien tilalle muodostuu kuusikulmioita rajaava neliö. Koska jokaisessa alkuperäisen oktaedrin kärjessä kohtasi neljä särmää, syntyneet uudet pinnat ovat neliöitä.
Pinta-ala (säännölliselle särmälle a)
Jos kappaleen särmä on pituudeltaan a ja sekä kuusikulmiot että neliöt ovat säännöllisiä, pinta-ala saadaan laskemalla yhteen kaikkien pintojen alat:
- Yhden säännöllisen kuusikulmion ala = (3√3 / 2) a²
- Yhden neliön ala = a²
- Kokonaispinta-ala S = 8·(3√3 / 2)a² + 6·a² = (12√3 + 6) a²
Käyttö ja esiintyminen
Lyhennetty oktaedri esiintyy teoreettisissa ja käytännön sovelluksissa, joissa tarvitaan tilajaotusta tai monimuotoista, mutta säännöllistä tilarakennetta. Sen kyky täyttää avaruus ilman rakoja tekee siitä kiinnostavan mallin esimerkiksi materiaalitutkimuksessa, kide- ja huokosrakenteiden tutkimuksessa sekä joidenkin mekaanisten ja arkkitehtonisten rakenteiden suunnittelussa. Lisäksi se on suosittu esimerkki geometrisissa kuvioissa ja opetuksessa arkimedealaisista kappaleista.
Kuusikulmioista ja neliöistä koostuva typistetty oktaedri.
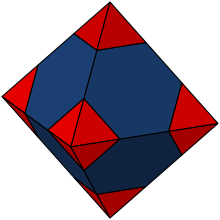
Lyhennetyn oktaedrin rakentaminen tapahtuu leikkaamalla punaisella merkityt osat, jotka ovat pyramideja, ja korvaamalla ne neliöillä.
