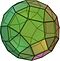
Arkhimedeen kappale

Geometriassa arkimedealainen kappale on monikulmioista koostuva kupera muoto. Se on polyedri, jolla on seuraavat ominaisuudet:

Kukin pinta on säännöllinen monikulmio.
Muodon kaikki kulmat näyttävät samoilta.
Muoto ei ole platoninen kiinteä kappale, prisma eikä antiprisma.

Laskutavasta riippuen tällaisia muotoja on kolmetoista tai viisitoista. Kahdesta näistä muodoista on kaksi versiota, joita ei voida tehdä yhteneväisiksi kiertämällä. Arkhimedeen kiinteät kappaleet on nimetty muinaiskreikkalaisen matemaatikon Arkhimedeen mukaan, joka todennäköisesti löysi ne 3. vuosisadalla eaa. Arkhimedeen kirjoitukset ovat kadonneet, mutta Pappus Aleksandrialainen teki niistä yhteenvedon 4. vuosisadalla. Renessanssin aikana taiteilijat ja matemaatikot arvostivat puhtaita muotoja ja löysivät kaikki nämä muodot uudelleen. Johannes Kepler saattoi tämän etsinnän todennäköisesti päätökseen noin vuonna 1620.

Arkhimedeen kiinteän kappaleen rakentamiseen tarvitaan vähintään kaksi erilaista monikulmiota.

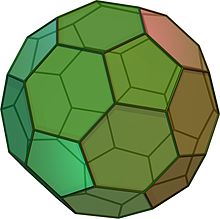
Lyhennetty ikosaedri näyttää jalkapallopallolta. Se koostuu 12 tasasivuisesta viisikulmiosta ja 20 säännöllisestä kuusikulmiosta. Sillä on 60 kärkeä ja 90 reunaa. Se on arkimedealainen kappale

Ominaisuudet

Arkhimedealaiset kappaleet koostuvat säännöllisistä monikulmioista, joten kaikki reunat ovat yhtä pitkiä.
Kaikki arkimedealaiset kiinteät kappaleet voidaan tuottaa platonisista kiinteistä kappaleista leikkaamalla platonisen kiinteän kappaleen reunoja.
Kulmassa ("kärjessä") kohtaavien monikulmioiden tyyppi on ominaista sekä arkimedealaiselle että platoniselle kiinteälle kappaleelle.

Suhde platonisiin kiinteisiin kappaleisiin

Platoniset kiinteät kappaleet voidaan muuttaa arkimedealaisiksi kiinteiksi kappaleiksi noudattamalla niiden rakentamista koskevia sääntöjä.

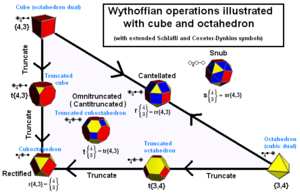
Arkhimedealaiset kiinteät kappaleet voidaan rakentaa kaleidoskoopin generaattoripaikoiksi.

Luettelo arkimedealaisista kappaleista

Seuraavassa luetellaan kaikki arkimedealaiset kiinteät kappaleet.

Kuva	Nimi	Kasvot	Tyyppi	Reunat	Verteksit
	Lyhyt tetraedri	8	4 kolmiota 4 kuusikulmiota	18	12
	Cuboctahedron	14	8 kolmiota 6 ruutua	24	12
	Katkaistu kuutio	14	8 kolmiota 6 kahdeksankulmaista	36	24
	Lyhennetty oktaedri	14	6 ruutua 8 kuusikulmiota	36	24
	Rhombicuboctahedron	26	8 kolmiota 18 ruutua	48	24
	Lyhennetty kuutioktaedri	26	12 ruutua 8 kuusikulmiota 6 kahdeksankulmaista	72	48
	Snub cube (2 peiliversiota)	38	32 kolmiota 6 ruutua	60	24
	Ikosidodekaedri	32	20 kolmiota 12 viisikulmioita	60	30
	Lyhennetty dodekaedri	32	20 kolmiota 12 desagonia	90	60
	Katkaistu ikosaedri	32	12 viisikulmioita 20 kuusikulmiota	90	60
	Rombikosidodekaedri	62	20 kolmiota30 neliötä12 viisikulmiota	120	60
	Lyhennetty ikosidodekaedri	62	30 ruutua 20 kuusikulmiota 12 desagonia	180	120
	Snub-dodekaedri (2 peiliversiota)	92	80 kolmiota 12 viisikulmioita	150	60

Kysymyksiä ja vastauksia

Kysymys: Mikä on arkimedealainen kiinteä kappale?

V: Arkhimedealainen kappale on monikulmioista koostuva kupera muoto, jonka ominaisuuksiin kuuluu, että jokainen pinta on säännöllinen monikulmio, kaikki kulmat näyttävät samalta ja että se ei ole platoninen kappale, prisma tai antiprisma.

Kysymys: Kuinka monta arkimedealaista kiinteää ainetta on olemassa?

V: Riippuen siitä, miten ne lasketaan, arkimedealaisia kiinteitä aineita on joko kolmetoista tai viisitoista.

K: Kuka löysi arkimedealaiset kiinteät kappaleet?

V: Arkhimedeen kiinteät kappaleet on nimetty muinaiskreikkalaisen matemaatikon Arkhimedeen mukaan, joka todennäköisesti löysi ne 3. vuosisadalla eaa.

K: Mitä Pappus Aleksandrialainen teki Arkhimedeen kirjoituksilla?

V: Pappus Aleksandrialainen teki yhteenvedon Arkhimedeen kiinteitä aineita koskevista Arkhimedeen kirjoituksista 4. vuosisadalla.

K: Miksi taiteilijat ja matemaatikot löysivät arkimedealaiset kiinteät kappaleet uudelleen renessanssin aikana?

V: Renessanssin aikana taiteilijat ja matemaatikot arvostivat puhtaita muotoja, ja Arkhimedeen kiinteitä aineita pidettiin puhtaina muotoina.

K: Milloin Johannes Kepler sai päätökseen kaikkien arkimedealaisten kiinteiden kappaleiden etsimisen?

V: Johannes Kepler sai todennäköisesti päätökseen kaikkien arkimedealaisten kiinteiden kappaleiden etsimisen noin vuonna 1620.

K: Mitä tarvitaan arkimedeeläisen kiinteän kappaleen rakentamiseen?

V: Arkhimedeen kiinteän kappaleen rakentamiseen tarvitaan vähintään kaksi erilaista monikulmiota.