Käyrän sovittaminen – määritelmä, interpolointi, regressio ja ekstrapolointi
Käyrän sovittaminen: opas interpolointiin, tasoitukseen, regressioon ja ekstrapolointiin — opi menetelmät, epävarmuudet ja käytännön sovellukset data-analyysissä.
Käyrän sovittaminen tarkoittaa sellaisen matemaattisen funktion muodostamista, joka sopii parhaiten tietopistejoukkoon. Käyrän sovittamisen tavoitteena on löytää yksinkertainen ja selkeä malli, joka kuvaa havaittua ilmiötä riittävän hyvin ja yleistyy myös uusiin tietoihin.
Käyrien sovittaminen voi sisältää joko interpolointia tai tasoitusta. Interpolointi pyrkii kulkemaan täsmälleen kaikkien havaintopisteiden kautta — sitä käytetään, kun mittausarvot oletetaan virheettömiksi tai kun halutaan tarkka funktio juuri annetuissa pisteissä. Tasoitus tai fitting tarkoittaa sen sijaan sitä, että muodostetaan "sileä" funktio, joka noudattaa aineistoa likimääräisesti ja ottaa huomioon mittausvirheet tai satunnaisuuden. Aiheeseen liittyy myös regressioanalyysi, jossa keskitytään enemmän tilastolliseen päättelyyn — esimerkiksi arvioimaan, kuinka paljon epävarmuutta on sovitetulla käyrällä, kun dataan liittyy satunnaisvirheitä.
Interpolointi – milloin ja miten
- Kun käyttää: pienet aineistot ilman merkittävää mittausvirhettä, signaalinkäsittely, kartografian korkeuskäyrät, tietokonegrafiikka.
- Menetelmät: polynominen interpolointi, Hermiten polynomi, B-splines ja kubiset splines, Sinc-interpolaatio tms.
- Huomioitavaa: korkean asteen polynomit voivat aiheuttaa värähtelyä (Runge-ilmiö). Numeraalisesti stabiilimmat vaihtoehdot kuten splines tai paikalliset interpolointimenetelmät ovat usein parempia käytännössä.
Regressio ja tasoitus
Regressio etsii parametrisen tai ei-parametrisen mallin, joka kuvaa muuttujien välistä riippuvuutta. Yleinen ja laajasti käytetty tapa on vähimmäisneliösovitus (ordinary least squares), jossa minimoidaan jäännösten (havainto − malli) neliösumma. Myös ei-lineaarinen regressio, splinet, LOESS/LOWESS ja koneoppimisen menetelmät (ks. päätöspuut, satunnaismetsät, neural-net) kuuluvat regressioon.
Tärkeitä käsitteitä:
- Jäännökset (residuals): erot havaintojen ja mallin ennusteiden välillä — niiden analysointi auttaa havaitsemaan mallin puutteita.
- Ylitasoitus ja alitasoitus: liian monimutkainen malli mallittaa myös kohinaa (ylitasoitus), liian yksinkertainen ei kuvaa ilmiötä hyvin (alitasoitus).
- Regulaaristus: menetelmät kuten ridge- ja lasso-regressio estävät ylitasoitusta rajoittamalla malliparametrien suuruutta.
- Hyvyyden mittarit: R² ja sen korjattu muoto, RMSE (root mean squared error), MAE (mean absolute error), AIC, BIC sekä ristikvalidointi (cross-validation) mallivalinnassa.
Ekstrapolointi ja sen riskit
Ekstrapolointi tarkoittaa sovitetun käyrän käyttöä havaintojen alueen ulkopuolella. Ekstrapolointi on aina epävarmempaa kuin interpolointi tai ennuste alueen sisällä, koska malli perustuu aineistoon ja voi muuttua nopeasti alueen ulkopuolella. Usein epävarmuutta kannattaa kvantifioida esimerkiksi ennusteväleillä tai simulaatiolla.
Käytännön ohjeita ja hyvä työtapa
- Visualisoi data ensin: hajontakuvio, aikasarja tai jäännösten kuvaaja paljastavat paljon.
- Aloita yksinkertaisella mallilla ja lisää kompleksisuutta vain tarpeen mukaan.
- Käytä ristikvalidointia arvioidaksesi mallin yleistyvyyttä ja välttääksesi ylioptimisointia.
- Tarkista jäännökset: eivät saisi olla järjestäytyneitä tai heteroskedastisia ilman syytä.
- Valitse numeerisesti stabiili menetelmä: esimerkiksi suora korkeiden asteen polynomien sovitus Vandermonde-matriisilla voi olla epästabiili — splines tai ortogonaaliset polynomit ovat usein parempia.
- Raportoi epävarmuus: parametriestimaatit, ennustevälit, standardipoikkeamat ja mahdolliset oletukset (normaalisuus, riippumattomuus).
- Harkitse robustia regressiota, jos aineistossa on poikkeavia havaintoja (outliers).
Yleisiä menetelmiä lyhyesti
- Lineaarinen regressio — yksinkertainen ja tulkittava, hyvä lähtökohta.
- Polynominen sovitus — joustava, mutta vaatii varovaisuutta korkeissa asteissa.
- Spline- ja piecewise-menetelmät — yhdistävät joustavuuden ja stabiilisuuden.
- LOESS/LOWESS — paikallinen regressio hyvälle käyrän pehmeydelle erityisesti aikasarjoissa.
- Nonparametrinen menetelmät ja koneoppiminen — kun mallin muotoa ei haluta määrittää etukäteen.
Yhteenvetona: käyrän sovittaminen on tehokas työkalu datan ymmärtämiseen, ennustamiseen ja visualisointiin, mutta menetelmän valinta ja epävarmuuden arviointi ovat ratkaisevia. Interpolointi sopii tarkkoihin pistekohtaisiin tarpeisiin, regressio ja tasoitus ottavat huomioon mittausvirheet ja tilastollisen epävarmuuden, ja ekstrapoloinnissa on aina varauduttava suurempaan epävarmuuteen.
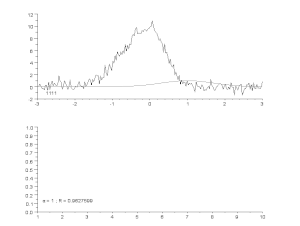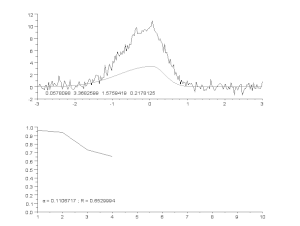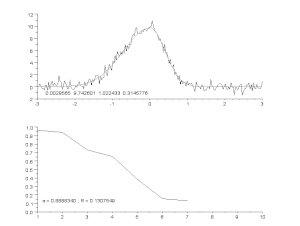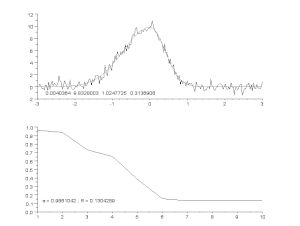
Epäsymmetrisen huippumallin sovittaminen meluiselle käyrälle iteratiivisella prosessilla (Gauss-Newton-algoritmi, jossa on muuttuva vaimennuskerroin α). Ylhäällä: raakadata ja malli. Alhaalla: virheiden neliöiden normalisoidun summan kehitys.
Kysymyksiä ja vastauksia
K: Mitä on käyränsovitus?
V: Käyrien sovittaminen on prosessi, jossa luodaan matemaattinen funktio, joka sopii parhaiten tietopistejoukkoon.
K: Mitä kahta tyyppiä käyrien sovittaminen on?
V: Käyrien sovittamisen kaksi tyyppiä ovat interpolointi ja tasoitus.
K: Mitä on interpolointi?
V: Interpolointi on käyränsovituksen tyyppi, joka edellyttää tarkkaa sovittamista tietoihin.
K: Mitä on tasoitus?
V: Tasoitus on käyrän sovituksen tyyppi, jossa muodostetaan "sileä" funktio, joka sopii tietoihin likimain.
K: Mitä on regressioanalyysi?
V: Regressioanalyysi on aiheeseen liittyvä aihe, jossa keskitytään tilastolliseen päättelyyn liittyviin kysymyksiin, kuten siihen, kuinka paljon epävarmuutta on käyrällä, joka on sovitettu satunnaisvirheillä havaittuihin tietoihin.
K: Mitä käyttötarkoituksia sovitetuilla käyrillä on?
V: Sovitettuja käyriä voidaan käyttää apuna tietojen havainnollistamisessa, funktion arvojen arvaamisessa, jos tietoja ei ole saatavilla, ja kahden tai useamman muuttujan välisten suhteiden tiivistämisessä.
K: Mitä on ekstrapolointi?
V: Ekstrapolointi on sovitetun käyrän käyttöä havaittujen tietojen alueen ulkopuolella. Tähän liittyy kuitenkin jonkin verran epävarmuutta, koska se voi heijastaa käyrän rakentamisessa käytettyä menetelmää yhtä paljon kuin havaittuja tietoja.
Etsiä