Funktio

Matematiikassa funktio on matemaattinen objekti, joka tuottaa tulosteen, kun sille annetaan tulo (joka voi olla luku, vektori tai mikä tahansa, joka voi olla joukon sisällä).

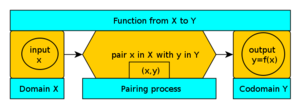
Funktio on siis kuin kone, joka ottaa arvon x ja palauttaa tulosteen y. Kaikkien arvojen joukkoa, joita x:llä voi olla, kutsutaan toimialueeksi, ja joukkoa, joka sisältää kaikki arvot, joita y:llä voi olla, kutsutaan koodialueeksi. Funktiota merkitään usein kursiivikirjaimilla, kuten f {\displaystyle f} , g {\displaystyle g} , h {\displaystyle h} $h$ .

Jos näin tapahtuu, sanomme, että y on x:n funktio, ja kirjoitamme y = f ( x ) {\displaystyle y=f(x)} $y=f(x)$ . Tässä f {\displaystyle f} on funktion nimi, ja kirjoitetaan f : X → Y {\displaystyle f:X\to Y} (funktio X:stä Y:hyn) kuvaamaan funktion kolmea osaa: toimialuetta (X), koodialuetta (Y) ja paritusprosessia (nuoli).

Esimerkki funktiosta on f ( x ) = x + 1 {\displaystyle f(x)=x+1} $f(x)=x+1$ . Annetaan syötteeksi luonnollinen luku x {\displaystyle x} ja saadaan luonnollinen luku y {\displaystyle y}. , joka on x + 1 {\displaystyle x+1} $x+1$ . Esimerkiksi antamalla f {\displaystyle f} syötteeksi 3 saadaan tulokseksi 4.

Funktion ei tarvitse olla yhtälö. Pääajatuksena on, että syötteet ja tuotokset yhdistetään jotenkin - vaikka prosessi saattaisikin olla hyvin monimutkainen.

Metaforat

Taulukot

Sisään- ja ulostulot voidaan sijoittaa kuvan kaltaiseen taulukkoon; tämä on helppoa, jos tietoja ei ole liikaa.

Graafit

Kuvassa näkyy, että sekä 2 että 3 on yhdistetty c:n kanssa; tämä ei ole sallittua toiseen suuntaan, koska 2 ei voisi antaa c:tä ja d:tä samaan aikaan (kullakin tulolla voi olla vain yksi lähtö). Kaikkia f ( x ) {\displaystyle f(x)} f(x) (kuvassa c ja d) kutsutaan yleensä f {\displaystyle f} kuvajoukoksi, ja kuvajoukko voi olla koko koodialue tai jokin sen osajoukko. Voidaan sanoa, että osa-alueen A osajoukon A kuvajoukko on f(A). Jos tuloilla ja lähdöillä on jokin järjestys, ne on helppo piirtää kuvaajaan:

Näin kuva tulee joukon A kuvaan.

Historia

Gottfried Leibniz ja Johann Bernoulli käyttivät 1690-luvulla sanaa "funktio" kirjaimilla välissä, joten nykyaikainen käsite sai alkunsa samaan aikaan laskennan kanssa.

Vuonna 1748 Leonhard Euler antoi funktiolle seuraavan määritelmän:

"Muuttuvan suureen funktio on analyyttinen lauseke, joka koostuu millään tavalla muuttuvasta suureesta ja luvuista tai vakiosuureista."

ja sitten vuonna 1755:

"Jos jotkin suureet ovat niin riippuvaisia toisista suureista, että jos jälkimmäisiä muutetaan, myös ensimmäiset muuttuvat, kutsutaan ensin mainittuja suureita jälkimmäisten funktioiksi. Tätä määritelmää sovelletaan melko laajasti, ja se kattaa kaikki tavat, joilla yksi suure voi määräytyä toisen suureen perusteella. Jos siis x tarkoittaa muuttuvaa suureen, niin kaikkia suureita, jotka jollakin tavalla riippuvat x:stä tai ovat sen määräämiä, kutsutaan x:n funktioiksi."

Yleensä Peter Dirichlet'n ansioksi luetaan ensimmäinen moderni funktion määritelmä (muotoiltu vuonna 1837). Sitä käytetään usein kouluissa 1900-luvun jälkipuoliskolle asti:

"y on muuttujan x funktio, joka on määritelty intervalliin a < x < b, jos jokaista muuttujan x arvoa tällä intervalliin kuuluvalla alueella vastaa muuttujan y tietty arvo. Lisäksi on yhdentekevää, millä tavalla tämä vastaavuus on todettu."

Vuonna 1939 Bourbaki yleisti Dirichlet'n määritelmää ja antoi määritelmästä joukko-opillisen version, joka on tulojen ja lähtöjen välinen vastaavuus; tätä käytettiin kouluissa noin vuodesta 1960 lähtien.

Vuonna 1970 Bourbaki antoi lopulta nykyaikaisen määritelmän kolmikkona f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} , jossa F ⊂ X × Y , ( x , f ( x ) ) ∈ $F\subset X\times Y,(x,f(x))\in F$ (eli f : X → Y {\displaystyle f:X\to Y} ja F = { ( x , f ( x ) ) ) ∣ x ∈ X , f ( x ) ∈ $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X:ää$ kutsutaan $f:$ n alueeksi, $Y:tä$ sen koodialueeksi ja $F:ää$ sen kuvaajaksi. Kaikkien niiden alkioiden joukkoa, jotka ovat muotoa $f (x),$ jossa $x$ ulottuu alueen $X$ alkioiden yli, kutsutaan $f:$ n kuvaksi. Funktion kuva on sen koodialueen osajoukko, eikä se välttämättä ole yhteneväinen sen kanssa.

Toimintatyypit

Alkeisfunktiot - Funktiot, joita yleensä opiskellaan koulussa: murtoluvut, neliöjuuret, sini-, kosini- ja tangenttifunktiot sekä joitakin muita funktioita.
Muut kuin alkeisfunktiot - Useimmat niistä käyttävät operaatioita, joita emme opi koulussa (kuten + tai - tai potensseja). Esimerkiksi monet integraalit eivät ole alkeisfunktioita.
Käänteisfunktiot - funktiot, jotka kumoavat toisen funktion. Esimerkiksi: Jos F(x) on käänteisfunktio f(x)=y, niin F(y)=x. Kaikilla funktioilla ei ole käänteisfunktioita.
Erityistoiminnot: Toiminnot, joilla on nimi. Näitä ovat trigonometriset funktiot, kuten sini, kosini ja tangentti. Funktioita kuten f(x)=3x (kolme kertaa x) ei kutsuta erikoisfunktioiksi. Erityisfunktiot voivat olla alkeisfunktioita, ei-alkiofunktioita tai käänteisfunktioita.

Aiheeseen liittyvät sivut

Vakiotoiminto
Jatkuva funktio
Toiminnon koostumus
Erityistoiminnot

Gamma-funktio
Matriisitoiminto

Lineaarinen funktio
Lucy Joan Slater - brittiläinen matemaatikko, joka tutki matemaattisia funktioita.
MATLAB, Wolfram Mathematica - ohjelmistot matemaattisten funktioiden laskemiseen.
Suhde (matematiikka)

Kysymyksiä ja vastauksia

K: Mikä on funktio matematiikassa?

V: Funktio on matematiikassa objekti, joka tuottaa tulosteen, kun sille annetaan tulo, joka voi olla luku, vektori tai mikä tahansa, joka voi olla joukon sisällä.

K: Mitkä kaksi joukkoa liittyvät funktioihin?

V: Kaikkien niiden arvojen joukkoa, joita x:llä voi olla, kutsutaan toimialueeksi, ja joukkoa, joka sisältää kaikki arvot, joita y:llä voi olla, kutsutaan yhteistoiminta-alueeksi.

K: Miten funktioita usein merkitään?

V: Funktioita merkitään usein kursiivikirjaimilla, kuten f, g, h.

K: Miten esitämme funktion?

V: Esitämme funktion kirjoittamalla y = f(x), jossa f on funktion nimi ja kirjoitetaan f : X → Y (funktio X:stä Y:hen), jotta voidaan esittää funktion kolme osaa - toimialue (X), koodialue (Y) ja paritusprosessi (nuoli).

Kysymys: Voitko antaa esimerkin funktiosta?

V: Esimerkki funktiosta on f(x) = x + 1. Annetaan syötteenä luonnollinen luku x ja saadaan luonnollinen luku y, joka on x + 1. Esimerkiksi antamalla f:lle syötteeksi 3 saadaan tulokseksi 4.

Kysymys: Pitääkö jokaisen funktion olla yhtälö?

V: Ei, jokaisen funktion ei tarvitse olla yhtälö. Funktioiden perusidea on, että syötteet ja tuotokset yhdistetään jotenkin - vaikka se olisikin hyvin monimutkaista.