Euler–Bernoullin palkkiteoria – periaatteet ja sovellukset

Euler–Bernoullin palkkiteoria — selkeä opas pienten taipumien laskentaan ja käytännön sovelluksiin kone- ja rakennustekniikassa. Periaatteet, esimerkit ja käyttöehdot.

Euler-Bernoullin palkkiteoria (tunnetaan myös nimellä insinöörien palkkiteoria tai klassinen palkkiteoria) on yksinkertainen menetelmä, jolla voidaan laskea palkkien taipuminen kuormituksen vaikutuksesta. Sitä sovelletaan palkin pieniin taipumiin (kuinka paljon jokin liikkuu) ottamatta huomioon leikkausmuodonmuutosten vaikutuksia. Siksi sitä voidaan pitää Timoshenkon palkkiteorian erikoistapauksena. Se esiteltiin ensimmäisen kerran noin vuonna 1750. Se sai suosiota Eiffel-tornin ja maailmanpyörän kehittämisen aikana 1800-luvun lopulla. Sen jälkeen sitä käytettiin monilla tekniikan aloilla, kuten kone- ja rakennustekniikassa. Vaikka muita kehittyneitä menetelmiä on kehitetty, Euler-Bernoullin palkkiteoriaa käytetään edelleen laajalti sen yksinkertaisuuden vuoksi. 

Perusperiaatteet

Euler–Bernoulli-mallin perusoletus on, että palkin poikkileikkauksen tasot pysyvät kohtisuorina keskiviivaan nähden myös taivutuksen jälkeen. Tämä tarkoittaa käytännössä, että poikkileikkaus säilyttää muotonsa (ei muutu vinoksi tai leikkaudu), ja poikkileikkauksen alkutasot pysyvät tasaisina (”plane sections remain plane”). Malli pätee parhaiten kapeille, pitkulaisille palkille, joissa taivutus on hallitseva muodonmuutos.

Keskeiset oletukset

• Pienet poikkeamat ja pieniä taipumia koskeva lineaarinen teoria (geometrinen lineaarisuus).
• Poikkileikkausten pysyminen tasaisina ja kohtisuorina keskiviivaan nähden.
• Materiaali on elastista ja Hooken lain mukaista (lineaarinen jännitys–venymä-suhde), homogeenista ja isotrooppista.
• Leikkausmuodonmuutuksia (shear deformation) ei oteta huomioon.

Perusyhtälöt ja suureet

Keskeisiä suureita ja yhtälöitä (yksidimensioinen palkkiteoria, x-akseli palkin pituussuunnassa):

• Bendin momentti: M(x).
• Taipuma (poikkeama keskiviivasta): w(x) (usein merkitty v(x) myös).
• Jäykkyys: EI, jossa E on materiaalin kimmokerroin ja I poikkileikkauksen toinen momentti.
• Kuorman tiheys: q(x) (voima per pituusyksikkö).

Perusyhtälö (vakio EI):
EI · d^4w/dx^4 = q(x).
Momentin ja taivutuksen yhteys (kaarevuus):
M(x) = -EI · d^2w/dx^2.
Taivutusjännitys poikkileikkauksessa:
σ_x = -M·y / I, missä y on etäisyys neutraalitasosta.

Voiman ja momentin yhteydet: dV/dx = -q(x) ja dM/dx = V(x), missä V on leikkausvoima. Näistä seuraa usein käytetty differentiaaliyhtälö d^2M/dx^2 = -q(x).

Sovellukset

Euler–Bernoulli-teoriaa käytetään laajasti perinteisissä rakennus- ja koneteknisissä laskelmissa, kuten:

• Lattiapalkit, palkkirakenteet ja sillat.
• Koneenosien varret, akselit ja tukielementit, joissa leikkausvaikutus on pieni verrattuna taivutukseen.
• Alustavat mitoittelu- ja käsinlaskelmat, opetus ja yksinkertaiset simulointielementit.
• FEM-mallinnuksessa käytetään usein Euler–Bernoulli-tyyppisiä palkkielementtejä, erityisesti kun halutaan tarkka taivutuskäyttäytymisen kuvaus ilman leikkausvaikutuksia.

Rajoitukset ja parannukset

Euler–Bernoulli-malli ei sovellu hyvin tilanteisiin, joissa:

• Palkki on lyhyt ja paksu (leikkausmuodonmuutukset merkittäviä) — tällöin Timoshenkon palkkiteoria on parempi vaihtoehto, koska se ottaa huomioon leikkausvenymät.
• Taipumat ovat suuria niin, että geometrinen ei-lineaarisuus (muodonmuutosvaikutukset) tulee merkittäviksi.
• Materiaali ei ole homogeeninen tai käyttäytyy epälineaarisesti (plastisuus, viskoelastisuus).

Myös FEM-kontekstissa Euler–Bernoulli-elementit voivat kärsiä ns. vaimennus- tai lukkiutumisongelmista (shear locking) tietyissä diskretoinneissa, jolloin Timoshenko-tyyppiset elementit tai hienompi verkotus ovat parempia.

Esimerkki: kannattamaton tukipalkki (cantilever) pistokuormalla

Yksinkertainen esimerkki: palkki pituudella L, päässä pistekuorma P. Maksimitaipuma vapaassa päässä on

w_max = P L^3 / (3 E I)

Tämä tulos saadaan integroimalla perusyhtälöä ja soveltamalla reunaehtoja (kiinnitys x=0: w=0, slope=0). Samankaltaisissa yksinkertaisissa tapauksissa löytyy suljetun muodon ratkaisuja myös tuetuissa paikoissa (esim. keskiraskauden alainen yksinkertaisesti tuettu palkki: w_max = P L^3 / (48 E I) pistekuormalle keskellä).

Lyhyt historiateko ja huomautuksia

Nimi tulee Leonhard Eulerilta ja Daniel Bernoullilta, jotka kehittivät teoriaa 1700-luvulla. Eulerin ja Bernoullin perusajatukset muodostavat edelleen perustan monille nykyaikaisille rakenneanalyysin menetelmille. Vaikka moderni suunnittelu ja numeeriset menetelmät (kuten monimutkaiset FEM-mallit) tarjoavat tarkempia kuvauksia vaikeista tilanteista, Euler–Bernoulli-palkkiteoria on yhä hyödyllinen ja opettavainen lähtötaso ja usein riittävä moniin käytännön mitoituksiin.

Historia

Leonhard Euler ja Daniel Bernoulli kokosivat teorian ensimmäisenä vuonna 1750. Tuohon aikaan tieteeseen ja tekniikkaan suhtauduttiin eri tavalla kuin nykyään. Eulerin ja Bernoullin palkkiteorian kaltaisiin matemaattisiin teorioihin ei luotettu käytännön insinöörikäytössä. Siltoja ja rakennuksia suunniteltiin edelleen samoilla menetelmillä aina 1800-luvun lopulle asti. Tällöin Eiffel-torni ja maailmanpyörä osoittivat teorian pätevyyden laajemmassa mittakaavassa.

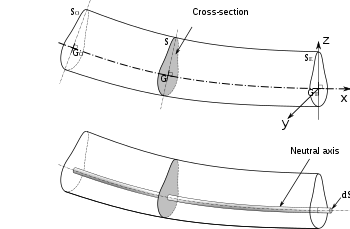
Piirustus taivutetun palkin poikkileikkauksesta, jossa näkyy neutraaliakseli.

Staattisen palkin yhtälö

Euler-Bernoullin yhtälö kuvaa palkin taipuman ja käytetyn kuorman välistä suhdetta seuraavasti:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,}

missä w ( x ) {\displaystyle w(x)} kuvaa palkin taipumaa z-suunnassa jossakin kohdassa x {\displaystyle x} . q {\displaystyle q} on hajautettu kuorma, toisin sanoen voima pituusyksikköä kohti (analogisesti paineen kanssa, joka on voima pinta-alaa kohti); se voi olla funktio seuraavista arvoista: x {\displaystyle x} , w {\displaystyle w} , w {\displaystyle w} . tai muita muuttujia.

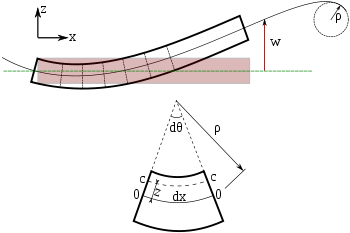
Euler-Bernoulli-palkin taivutus. Palkin jokainen poikkileikkaus on 90 astetta neutraaliakseliin nähden.

Kysymyksiä ja vastauksia

K: Mikä on Euler-Bernoullin palkkiteoria?

K: Milloin Euler-Bernoullin palkkiteoria otettiin ensimmäisen kerran käyttöön?

K: Käytettiinkö Euler-Bernoullin palkkiteoriaa Eiffel-tornin ja maailmanpyörän kehittämisessä?

K: Millä tekniikan aloilla Euler-Bernoullin palkkiteoriaa on käytetty?

Kysymys: Onko Euler-Bernoullin palkkiteoria edelleen laajalti käytössä?

K: Minkälaisiin palkin taipumiin Euler-Bernoullin palkkiteoriaa sovelletaan?

K: Otetaanko Euler-Bernoullin palkkiteoriassa huomioon leikkausmuodonmuutosten vaikutukset?

Hae kirjaimella