Epäyhtälö
Epätasa-arvo on sitä, että yksi esine on:
- pienempi kuin toinen ( a < b {\displaystyle \ a<b} tarkoittaa
, että a on pienempi kuin b). - suurempi kuin toinen ( a > b {\displaystyle \ a>b} tarkoittaa
, että a on suurempi kuin b). - ei pienempi kuin toinen ( a ≥ b {\displaystyle a\geq b}
tarkoittaa, että a ei ole pienempi kuin b, eli se on joko suurempi tai yhtä suuri kuin b). - ei suurempi kuin toinen ( a ≤ b {\displaystyle a\leq b}
tarkoittaa, että a ei ole suurempi kuin b, tai se on pienempi tai yhtä suuri kuin b).
Epätasa-arvoa käytetään joskus nimittämään lausumaa, jonka mukaan yksi lauseke on pienempi, suurempi, ei pienempi tai ei suurempi kuin toinen.
Työskentely epätasa-arvojen kanssa
Matematiikassa epätasa-arvo tarkoittaa sitä, että kahta ratkaisua tai vastausta verrataan suuremmalla tai pienemmällä kuin. Se on silloin, kun kaksi tai vielä monta ratkaisua verrataan ei ole yhtä paljon. Epäyhtälön ratkaiseminen tarkoittaa sen ratkaisujen löytämistä. Kun korvaat muuttujan luvulla ja lauseke on tosi, se on ratkaisu. Kun korvataan luku muuttujalla ja väite ei ole tosi, silloin luku ei ole väitteen ratkaisu.
Epäyhtälö on ratkaisun löytäminen tietylle muuttujalle. Se on joukon suhteellisen järjestyksen löytämistä. Epäyhtälöllä on monia ratkaisuja, mutta sinun on löydettävä todelliset ratkaisut. Epäyhtälö on reaalilukujen ratkaisemista. Oikea tapa lukea epätasa-arvoja on vasemmalta oikealle, aivan kuten muitakin yhtälöitä, mutta ainoa ero on se, että niillä on erilaiset säännöt jokaiselle yhtälölle.
Esimerkiksi x+4>12, jossa x on reaaliluku. Ensin on löydettävä x ja tiedettävä, onko se ratkaisu. Vastaus on x>8 ja se on tosi väite. Tämä lauseke kertoo x:n sijainnin reaalilukujen joukossa. Lukujono on yksi tapa osoittaa sijainti suhteessa kaikkiin muihin reaalilukuihin (ks. kuva Epäyhtälö 1).
Epäyhtälö 1 Tämä on yhtälön x+4>12 ratkaisu.
Erilaisia epätasa-arvoja
On olemassa viisi erilaista eriarvoisuutta:
- Ensimmäinen on lineaariset epätasa-arvot, jotka ovat epätasa-arvo, joka erottaa lausekkeet joko pienemmällä tai yhtä suurella, pienemmällä tai suuremmalla tai suuremmalla, suuremmalla kuin. Se on yksi, että jos korvaamme epätasa-arvon yhtäsuuruus suhteella, niin lopputulos on lineaarinen yhtälö.
- Toinen on epätasa-arvojen yhdistelmät, jotka täyttääkseen epätasa-arvot, sinun on oltava numero ratkaisujoukoissa niin, että epätasa-arvot täyttävät numerot ovat kahden ratkaisujoukon risteyksessä olevia arvoja.
- Kolmas on epätasa-arvot, joihin liittyy absoluuttisia arvoja, mikä tarkoittaa, että arvot voidaan muotoilla uudelleen sellaisten epätasa-arvojen yhdistelmiksi, joihin liittyy absoluuttisia arvoja.
- Neljäs on nimeltään polynomi epätasa-arvot tarkoittaa, että se on jatkuva, se tarkoittaa, että niiden kuvaajat eivät ole mitään hyppyjä tai taukoja.
- Viimeisenä, mutta ei vähäisimpänä, on rationaalinen epätasa-arvo, mikä tarkoittaa, että se on yhden polynomin muoto jaettuna polynomilla. Toisin sanoen rationaalifunktion kuvaajissa ei ole taukoja eikä niitä esitetä nimittäjän nollakohdissa.
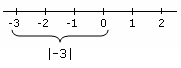
absoluuttinen arvo Esimerkki, joka osoittaa absoluuttisen arvon
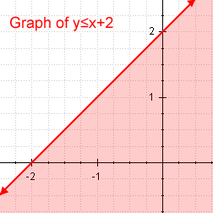
Lineaarinen epätasa-arvo Esimerkki lineaarisesta epätasa-arvosta
Neljä tapaa ratkaista epätasa-arvoja
Neliöyhtälöitä voidaan ratkaista neljällä eri tavalla:
- Sääntö numero yksi on, että sinun on lisättävä tai vähennettävä sama luku molemmilla puolilla.
- Sääntö numero kaksi on, että sinun on siirrettävä sivuja ja muutettava epätasa-arvon merkin sijaintia.
- Sääntö numero kolme on, että sinun on kerrottava.
- Neljäs sääntö on jakaa sama positiivinen tai negatiivinen luku molemmille puolille. Näitä sääntöjä voi kuitenkin käyttää vain helppoihin epätasa-arvo-ongelmiin.
Lisäksi epätasa-arvon ratkaisemiseen tarvitaan kaksi askelta. Ensimmäinen on yksinkertaistaminen käyttämällä yhteen- tai vähennyslaskun käänteislukua. Toisessa vaiheessa yksinkertaistetaan vielä enemmän käyttämällä kerto- tai jakolaskun käänteislukua. Kun kerrot tai jaat epäyhtälön negatiivisella luvulla, muista kääntää epäyhtälön symboli.
esimerkki eriarvoisuuden kertymisestä
Esimerkki epätasa-arvojen lisäämisestä.
Esimerkkejä epätasa-arvojen ratkaisemisesta
Epäyhtälö on matemaattinen lausuma, joka selittää, että kaksi arvoa eivät ole yhtä suuria ja erilaisia. Yhtälö ab tarkoittaa, että a ei ole yhtä suuri kuin b. Epäyhtälö on sama kuin mikä tahansa yhtälö, mutta ainoa ero on se, että epäyhtälö ei käytä yhtäsuuruusmerkkiä vaan symboleja. Epäyhtälö b>a tarkoittaa, että b on suurempi kuin a. Nopeusrajoitukset,merkki ja muut käyttävät epäyhtälöä ilmaisemaan niitä.
Kun ratkaista epätasa-arvo henkilö tarvitsee olla totta lausuma. Kun jaat tai kerrot epätasa-arvon, jonka molemmilla puolilla on negatiivinen luku, lausuma on epätosi.Jotta lausuma olisi oikea negatiivisen luvun kanssa, sinun on käännettävä symboli, jotta lausuma olisi oikea. Kun luku on positiivinen luku, sinun ei tarvitse kääntää symbolia. Epätasa-arvossa on kyse oikean väitteen tekemisestä.
Aloita esimerkiksi totuuslauseella -6y<-12. Kun molemmat puolet jaetaan -6:lla, tulokseksi tulee y<2. Tässä lausumassa symboli on käännettävä toisinpäin, jotta saadaan tosi lausuma, y>2 on oikea vastaus. Lukujonossa (ks. kuva Epäyhtälö 2) suljettu tummennettu ympyrä osoittaa, että se sisältyy ratkaisujoukkoon. Avoin ympyrä osoittaa, että se ei sisälly ratkaisujoukkoon.
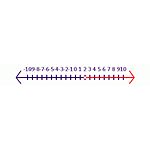
Epäyhtälö 2 Ratkaisu yhtälölle -6y<-12
Aiheeseen liittyvät sivut
- Yhtäläisyys (matematiikka)
- Yhtälö
Kysymyksiä ja vastauksia
K: Mitä tarkoittaa "a < b"?
V: Se tarkoittaa, että a on pienempi kuin b.
K: Mitä tarkoittaa "a > b"?
V: Se tarkoittaa, että a on suurempi kuin b.
K: Mitä tarkoittaa "a ≥ b"?
V: Se tarkoittaa, että a ei ole pienempi kuin b, eli se on joko suurempi tai yhtä suuri kuin b.
K: Mitä tarkoittaa "a ≤ b"?
V: Se tarkoittaa, että a ei ole suurempi kuin b, tai se on pienempi tai yhtä suuri kuin b.
K: Miten eriarvoisuutta voidaan käyttää matematiikassa?
V: Epäyhtälöä voidaan käyttää nimeämään väite, jonka mukaan toinen lauseke on pienempi, suurempi, ei pienempi tai ei suurempi kuin toinen.
