Kuutio — määritelmä, geometria ja kaavat: pinta-ala ja tilavuus
Tutustu kuution määritelmään, geometriaan ja selkeisiin kaavoihin: pinta-ala 6l², sivupinta-ala 4l² ja tilavuus l³. Selkeät esimerkit ja laskukaavat.
Kuutio on kappale, jonka kaikki kulmat ovat suorat ja jonka korkeus, leveys ja syvyys ovat kaikki samat.
Kuutio on yksi yksinkertaisimmista matemaattisista muodoista avaruudessa ja erikoistapaus suorakulmaista särmiötä (parallelepipedistä), missä kaikki särmien pituudet ovat yhtä suuria. Kuutiota kutsutaan myös säännölliseksi kuusikulmioksi tai säännölliseksi heksaedraksi (engl. cube, regular hexahedron) ja se on yksi viidestä Platonisesta kappaleesta.
Perusominaisuudet
- Kasvojen määrä: 6 (kaikki ovat neliöitä).
- Särmien määrä: 12.
- Huippujen määrä: 8.
- Eulerin lauseen tarkistus: V − E + F = 8 − 12 + 6 = 2.
- Kuution sivu (reuna) merkitään yleensä l (length).
- Kuution symmetria: rotaatioryhmän koko on 24 (täydellinen symmetriaryhmä heijastuksineen on 48).
- Kuution netit (avattuna tasoon taitetut pinnat): on olemassa 11 erilaista nettimuotoa.
Keskeiset kaavat ja johtaminen
Kaavoissa l tarkoittaa kuution sivun pituutta.
- Kokonaispinta-ala (A): A = 6 l2. Perustelu: kuutiossa on 6 neliöpintaa, jokaisen pinta-ala on l2.
- Sivupinta-ala (As): As = 4 l2. Huom. Termi "sivupinta-ala" tarkoittaa yleensä neljän sivun (ei ylä- ja alapuolen) yhteispinta-alaa, esimerkiksi kun kuutio asetetaan yhden neliöpohjan päälle.
- Tilavuus (V): V = l3. Perustelu: tilavuus = pohjan ala × korkeus = l2 × l = l3.
- Kulmadiagonali (kasvotason diagonaali): dkasvo = l√2. Johtuu Pythagoraan lauseesta kahdelle sivulle neliössä: √(l2 + l2) = l√2.
- Tila- eli lävistäjädiagonali (avaruusdiagonaali): d = l√3. Johtuu kolmiulotteisesta Pythagoraan lauseesta: √(l2 + l2 + l2) = l√3.
Yksinkertainen esimerkki
Olkoon kuution sivu l = 2 cm.
- Pinta-ala A = 6 × 22 = 6 × 4 = 24 cm2.
- Sivupinta-ala As = 4 × 22 = 16 cm2.
- Tilavuus V = 23 = 8 cm3.
- Kasvotason diagonaali dkasvo = 2√2 ≈ 2,828 cm.
- Tila- eli lävistäjädiagonali d = 2√3 ≈ 3,464 cm.
Käytännön näkökulmia ja sovelluksia
- Kuutiomuotoisia kappaleita käytetään usein pakkaamisessa ja rakennusmateriaalien muotoilussa, koska ne kasaantuvat tiiviisti.
- Kuution symmetriat ovat tärkeitä esimerkiksi kiteiden ja molekyylien mallinnuksessa sekä tietojenkäsittelyssä (3D-kartat, voxelit).
- Geometriassa kuutio on hyödyllinen esimerkki, kun opetellaan pinta-ala- ja tilavuuslaskuja sekä kolmiulotteisten diagonaalien laskemista.
Lisätietoa
Kuution käsitteitä ja kaavoja kannattaa harjoitella piirtämällä kuution netti ja laskemalla pinta-alat erikseen kullekin neliölle. Kun sivun pituus annetaan yksikössä x, pinta-alojen yksiköt ovat x2 (esim. cm2) ja tilavuuden yksikkö x3 (esim. cm3).
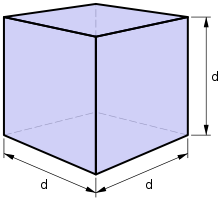
Kuutiolla on 6 yhtä pitkää ja leveää sivua.

Suurennettu suolakide
Suhteellinen 2-ulotteinen muoto
Kuution ja neliön välinen perusero on se, että kuutio on kolmiulotteinen hahmo (3 ulottuvuutta) eli pituus, leveys ja korkeus, kun taas neliöllä on vain 2 ulottuvuutta eli pituus ja leveys. Kaksiulotteinen (2D) muoto (kuten ympyrä, neliö, kolmio jne.), josta kuutio on tehty, on neliö. Kuution sivut (pinnat) ovat neliöitä. Reunat ovat suoria viivoja. Kulmat (kärjet) ovat suorassa kulmassa. Kuutiossa on 8 kulmaa, 12 reunaa ja 6 sivua, kuten tavallisimmassa nopassa. Tesseraktissa tämä ajatus viedään neljänteen ulottuvuuteen (4D), ja se koostuu 8 kuutiosta.
Volume
- Kuution tilavuus on minkä tahansa reunan pituus kuutioituna (ne ovat kaikki samanpituisia, joten ei ole väliä, mitä reunaa käytetään).
- Tämä tarkoittaa, että luku kerrotaan ensin itsellään ja sitten uudelleen itsellään.
- Jos reuna on nimeltään d (ks. kaavio), yhtälö on seuraava: Tilavuus=d×d×d (tai Tilavuus=d3 ).
Kuution muotoiset hahmot
- Noppa
- Laatikot
Kysymyksiä ja vastauksia
K: Mikä on kuutio?
A: Kuutio on eräänlainen monikulmio, jonka kaikki kulmat ovat suorat ja jonka korkeus, leveys ja syvyys ovat kaikki samat.
K: Mikä on suorakulmainen prisma?
A: Suorakulmainen prisma on heksaedrin tyyppi ja kolmiulotteinen muoto, jossa on kuusi suorakulmaista sivua.
K: Mikä on kuution pinta-ala?
V: Kuution pinta-ala on kuusi kertaa sivun pituus neliössä (6l^2).
K: Mikä on kuution sivupinta-ala?
V: Kuution sivupinta-ala on yhtä suuri kuin 4 kertaa sivun pituus neliössä (4l^2).
K: Mikä on kuution tilavuus?
V: Kuution tilavuus on yhtä suuri kuin sivun pituus kuutioituna (l^3).
K: Onko kuutio monimutkainen matemaattinen muoto?
V: Ei, kuutio on yksi yksinkertaisimmista matemaattisista muodoista avaruudessa.
K: Mitä kutsutaan kuution muotoiseksi esineeksi?
V: Kuution muotoista asiaa kutsutaan joskus kuutioksi.
Etsiä