Ulottuvuus määritelmä ja esimerkit 2D 3D 4D sekä vektoriavaruus

Mitat ovat tapa, jolla näemme, mittaamme ja koemme maailmamme: ylös ja alas, oikealta vasemmalle, takaa eteen, sekä ominaisuuksia kuten kuumaa ja kylmää, painavuutta ja pituutta. Mittoja käytetään sekä arkikokemuksessa että matematiikan ja fysiikan kehittyneemmässä kuvauksessa. Yksi tapa määritellä ulottuvuus on tarkastella vapausasteita eli sitä, kuinka monessa eri suunnassa jokin esine tai järjestelmä voi liikkua. Termillä "ulottuvuus" on useita käyttömerkityksiä: geometrinen, fysikaalinen, ja matemaattinen määritelmä eivät aina ole täysin samanlaisia.

Mitä ulottuvuus tarkoittaa käytännössä?

Helposti ymmärrettävä ajatus on, että ulottuvuus kertoo tarvittavien koordinaattien määrän sijainnin yksiselitteiseen kuvaamiseen. Esimerkiksi pisteen sijainti suoralla tarvitsee yhden luvun (1D), tasossa kaksi (2D) ja kolmiulotteisessa avaruudessa kolme (3D). Lisäksi ulottuvuus liittyy siihen, kuinka monta riippumatonta suuntaa muodostaa järjestelmän liikkeen mahdollisuudet (vapausasteet).

Esimerkkejä: 0D, 1D, 2D, 3D ja 4D

0D: yksittäinen piste. Ei etäisyyttä eikä suuntaa.
1D: suora tai viiva. Esine voi liikkua eteen- tai taaksepäin yhdellä akselilla.
2D: taso, kuten paperi tai näyttö. Tarvitaan kaksi koordinaattia (esim. x ja y) paikan kuvaamiseen.
3D: arkinen avaruus, jossa mitataan pituutta, leveyttä ja syvyyttä. Matemaatikkojen termi tälle on usein euklidinen avaruus.
4D: kun neljättä ulottuvuutta lisätään, sillä tarkoitetaan usein aikaa. Neljännellä ulottuvuudella kuvaillaan tapahtuman paikkaa sekä avaruudessa että ajassa — eli tapahtuman sijainti ajassa ja avaruudessa. Tämä johtaa käsitteeseen aika-avaruus, jota käytetään erityisesti suhteellisuusteoriassa.

Vektoriavaruuden ulottuvuus

Vektoriavaruudessa V {\displaystyle V} $V$ (jossa vektorit ovat "nuolia", joilla on suunnat), V {\displaystyle V}:n ulottuvuus on $V$ , joka kirjoitetaan myös nimellä dim ( V ) {\displaystyle \dim(V)} $\dim(V)$ , on yhtä suuri kuin V {\displaystyle V} $V$ -perustan kardinaalisuus (tai vektoreiden lukumäärä) (joukko, joka osoittaa, kuinka monta ainutkertaista suuntaa V {\displaystyle V} $V$ todella on). Se on myös yhtä suuri kuin kyseisen avaruuden suurimman suorien suuntien ryhmän lukumäärä. "Tavalliset" arkielämän esineet määritellään kolmella ulottuvuudella, joita kutsutaan yleensä pituudeksi, leveydeksi ja syvyydeksi. Matemaatikot kutsuvat tätä käsitettä euklidiseksi avaruudeksi.

Yksinkertaisesti sanottuna vektoriavaruuden dimensiolla tarkoitetaan sitä vähintään tarvittavien riippumattomien vektorien määrää, jolla kaikki avaruuden vektorit voidaan esittää lineaarikombinaationa. Esimerkiksi R2:n (tasovektorit) ulottuvuus on 2 ja R3:n ulottuvuus on 3. On myös äärettömänulotteisia avaruuksia, kuten polynomien avaruus, jossa perusjoukon koko on ääretön.

Mittaaminen, koordinaatit ja etäisyys

Mittoja voidaan käyttää myös sijainnin mittaamiseen. Etäisyys lähtöpaikasta mitataan usein pituus-, leveys- ja korkeussuunnassa. Koordinaatistot (esim. karteesiset koordinaatit x, y, z) antavat systeemin, jolla nämä etäisyydet ilmoitetaan numeerisesti. Etäisyyden mittaamisessa tarvitaan myös mittayksiköt (metri, kilometri jne.) ja etäisyyden määrittävä metriikka — esimerkiksi euklidinen etäisyys 3D-avaruudessa on suora etäisyys kahden pisteen välillä.

Fysiikassa ja vapausasteet

Fysiikassa ulottuvuuksia käytetään sekä paikan että liikkeen kuvaamiseen: yksittäisellä hiukkasella, joka voi liikkua pitkin suoraa, on yksi vapausaste; tasossa liikkuvalla hiukkasella on kaksi; ja kolmiulotteisessa avaruudessa kolme. Lukuisissa järjestelmissä tarvitaan muita muuttujia (esim. kulmat tai nopeudet), jolloin järjestelmän kokonaisvapausasteet voivat olla suurempia. Esimerkiksi jäykkä kappale vapaassa avaruudessa tarvitsee yleensä kuusi vapausastetta (kolme siirtoa ja kolme rotaatiota).

Korkeammat ulottuvuudet ja erikoistapaukset

Matemaatikot ja fyysikot käsittelevät usein myös yli kolmen ulottuvuuden avaruuksia, erityisesti teoreettisissa malleissa ja differentiaaliyhtälöiden tilatiloissa. Lisäksi on olemassa epäintegraalisia mittoja, kuten fraktaalinen ulottuvuus (esim. Hausdorffin dimensio), jotka kuvaavat monimutkaisten muotojen tilaa tavalla, joka ei aina ole kokonaisluku.

Yhteenveto

Ulottuvuus on käsite, joka kertoo, kuinka monella luvulla tai koordinaatilla paikan tai järjestelmän tila voidaan yksikäsitteisesti kuvata, sekä kuinka monta riippumatonta suuntaa liike voi saada. Käytännössä puhutaan 0D–3D arkitodellisuudesta ja usein 4D:stä, kun mukaan otetaan aika. Matemaattisesti ulottuvuus yleistyy vektoriavaruuksien dimensioon sekä monimutkaisempiin mittoihin kuten fraktaaliulottuvuuksiin.

Kaavio neljästä ensimmäisestä avaruusulottuvuudesta.

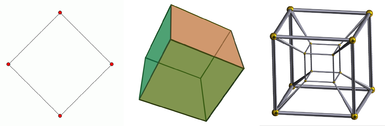
Vasemmalta oikealle: neliö, kuutio ja tesserakti. Neliö on kaksiulotteinen objekti, kuutio on kolmiulotteinen objekti ja tesserakti on neliulotteinen objekti. Yksiulotteinen objekti on vain viiva. Kuutiosta annetaan projektio, koska sitä tarkastellaan kaksiulotteisella näytöllä. Sama koskee tesseraktia, joka voidaan lisäksi esittää vain projektiona myös kolmiulotteisessa avaruudessa.

Muut mitat

Nykyaikaisessa tieteessä ihmiset käyttävät muita ulottuvuuksia. Lämpötilan ja painon kaltaisia ulottuvuuksia voidaan käyttää osoittamaan jonkin asian sijainti vähemmän yksinkertaisissa tiloissa. Tutkija tutkii näitä ulottuvuuksia ulottuvuusanalyysin avulla.

Myös matemaatikot käyttävät ulottuvuuksia. Matematiikassa ulottuvuudet ovat yleisempiä. Matematiikan ulottuvuudet eivät välttämättä mittaa maailmassa olevia asioita. Matematiikassa ulottuvuuksilla laskemisen säännöt voivat olla erilaisia kuin tavalliset aritmeettiset säännöt.

Mitat ja vektorit

Vektoreita käytetään etäisyyksien ja suuntien esittämiseen. Vektoreita käytetään usein tekniikassa ja luonnontieteissä sekä joskus matematiikassa.

Vektori on luettelo numeroita. Jokaista ulottuvuutta kohti on yksi numero. Vektoreille on olemassa aritmeettiset säännöt.

Jos esimerkiksi Jane haluaa tietää Sallyn sijainnin, Sally voi antaa Janelle vektorin, joka osoittaa sijainnin. Jos Jane ja Sally ovat maailmassa, maailmassa on kolme ulottuvuutta. Siksi Sally antaa Janelle kolmen numeron luettelon, joka osoittaa Janen sijainnin. Sallyn Janelle antaman vektorin kolme numeroa voivat olla:

Sallyn etäisyys Janesta pohjoiseen
Sallyn etäisyys Janesta itään
Sallyn korkeus Janen yläpuolella

Aiheeseen liittyvät sivut

3D
Hyperkuutio, neliön ja kuution yleistäminen kolmen ulottuvuuden ulkopuolelle.
Minkowskin avaruusaika, neliulotteinen monitaho
Avaruus-aika

Kysymyksiä ja vastauksia

Q: Mikä on ulottuvuus?

A: Mitta on tapa mitata, nähdä ja kokea maailma käyttämällä sellaisia käsitteitä kuin ylös ja alas, oikealta vasemmalle, takaa eteen, kuuma ja kylmä, kuinka raskas ja kuinka pitkä. Se voidaan määritellä myös vapausasteiksi tai tavaksi, jolla esine voi liikkua tietyssä tilassa.

K: Miten matemaatikot määrittelevät euklidisen avaruuden?

V: Matemaatikot määrittelevät euklidisen avaruuden siten, että siinä on kolme ulottuvuutta, joita kutsutaan yleensä pituudeksi, leveydeksi ja syvyydeksi.

K: Mikä on vektorien lukumäärä vektoriavaruudessa?

V: Vektorien lukumäärä vektoriavaruudessa on yhtä suuri kuin sen perusjoukon kardinaalisuus (tai vektoreiden lukumäärä).

K: Kuinka monta ulottuvuutta käytetään sijainnin mittaamiseen?

V: Sijainnin mittaamiseen käytetään kolmea ulottuvuutta (pituus, leveys ja korkeus). Joissakin tapauksissa voidaan käyttää neljättä (4D) ulottuvuutta - aikaa - osoittamaan tapahtuman sijainti ajassa ja avaruudessa.

K: Mitä dim(V) tarkoittaa?

V: Dim(V) tarkoittaa V:n ulottuvuutta, joka on yhtä suuri kuin sen perusjoukon kardinaalisuus (tai vektoreiden lukumäärä) tai yhtä suuri kuin sen suorien suuntien lukumäärä.

Kysymys: Onko olemassa yksi määritelmä, joka täyttää kaikki ulottuvuuksiin liittyvät käsitteet?

V: Ei, ei ole olemassa yhtä määritelmää, joka täyttäisi kaikki ulottuvuuksiin liittyvät käsitteet.