Ellipsi – määritelmä, yhtälö, polttopisteet ja esimerkit
Ellipsi: selkeä määritelmä, yhtälö ja polttopisteet käytännössä. Kaavat, esimerkit ja sovellukset geometriaan ja planeettojen ratoihin kätevästi yhdessä oppaassa.
Ellipsi on soikea tasokäyrä, joka muistuttaa litistynyttä ympyrää. Geometriassa ellipsi syntyy myös, kun kartio leikataan tasolla siten, että leikkaus on suljettu käyrä. Ympyrä on ellipsin erikoistapaus, joka saadaan, kun leikkaustaso on kohtisuorassa kartion akselia vastaan.
Määritelmä ja polttopisteet
Ellipsi voidaan määritellä joukona pisteitä tason alueella siten, että kunkin pisteen etäisyyksien summa kahdesta kiintopisteestä (polttopisteistä) on vakio. Jos polttopisteet ovat F1 ja F2 ja vakio on 2a, niin ellipsin pisteille P pätee PF1 + PF2 = 2a. Tästä seuraa, että ellipsillä on kaksi polttopistettä (toisin kuin ympyrällä, jolla on yksi keskipiste).
Polttopisteiden etäisyys keskipisteestä merkitään c:llä. Ellipsin puolisuuret akselit ovat a (puoliakseli pitkällä akselilla, eli semi-major axis) ja b (puoliakseli lyhyellä akselilla, eli semi-minor axis). Ne liittyvät toisiinsa kaavalla
c² = a² − b²,
missä a ≥ b ≥ 0. Ellipsin eksentrisyys e määritellään e = c / a, ja 0 ≤ e < 1 (e = 0 antaa ympyrän).
Yhtälö keskipisteessä ja koordinaateissa
Tasossa, kun ellipsin keskipiste on (h, k) ja pääakseli on x- tai y-suunnassa, standardimuotoinen yhtälö akselin suuntaiselle ellipsille on
((x − h)²) / a² + ((y − k)²) / b² = 1.
Alkuperäinen sivulla ollut kaavakuva ja -merkintä:
Ellipsin yhtälö on : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}}{b^{2}}}=1}
Yhtälössä a ja b ovat siis ellipsin puolisuuret akselit. Koko pääakselin pituus on 2a ja sivuakselin pituus 2b. Ellipsin kärkipisteet (vertexit) ovat (h ± a, k) ja (h, k ± b), riippuen kumpi akseli on pidempi.
Parametrinen esitys ja pinta-ala
Parametrisesti ellipsin pisteet voidaan esittää kulman t avulla:
x = h + a cos t, y = k + b sin t, t ∈ [0, 2π).
Ellipsin pinta-ala on
A = π a b.
Peilausominaisuus ja fysikaaliset sovellukset
Ellipsillä on tärkeä reflektio-ominaisuus: jokainen säde, joka lähtee toisesta polttopisteestä ja heijastuu ellipsin reunasta, kulkee toisen polttopisteen kautta. Tämä ominaisuus käytetään mm. akustiikassa ja optiikassa (esim. erikoismuotoiset peilit ja kuuluvuuskäytännöt).
Myös planeettojen radat aurinkokunnassa ovat ellipsejä: Keplerin ensimmäisen lain mukaan jokaisen planeetan rata on ellipsi, jonka toisessa polttopisteessä on aurinko.
Yleisempi yhtälö ja käännöt
Yleisin toisen asteen kaava conicille on muotoa Ax² + Bxy + Cy² + Dx + Ey + F = 0. Jos B ≠ 0, ellipsi voi olla kääntynyt (eli sen pääakseli ei ole koordinaattiakseleiden suuntainen). Tällöin voi tarvittaessa suorittaa rotaation ja siirron, jotta löytää ellipsin a, b, c ja keskipisteen.
Esimerkki
Otetaanko esimerkki: ellipsi keskellä origossa (h, k) = (0, 0) ja a = 5, b = 3. Silloin yhtälö on
x² / 25 + y² / 9 = 1.
Puolisuuret akselit: a = 5, b = 3. Polttopisteiden etäisyys keskipisteestä on c = √(a² − b²) = √(25 − 9) = √16 = 4. Polttopisteet ovat siis (±4, 0). Pisteen (3, 2) etäisyydet polttopisteisiin laskevat: √((3−4)² + 2²) + √((3+4)² + 2²) = √(1 + 4) + √(49 + 4) = √5 + √53 ≈ 2.236 + 7.280 ≈ 9.516 ≈ 2a = 10 (tässä tapauksessa arvo ei täsmää tarkasti, joten (3,2) ei ole ellipsillä). Ellipsin kärjet ovat (±5,0) ja (0,±3).
Rakentaminen
Perinteinen tapa piirtää ellipsi on niin kutsuttu "lankatekniikka": laitetaan kaksi nastaa polttopisteiden paikkoihin, kiinnitetään jousi tai langanpätkä nastojen ympärille siten, että langasta muodostuu silmukka, laitetaan lyijykynä silmukkaan ja pidetään lankaa kireällä. Liikuttamalla kynää langan kireyden säilyessä, kynä piirtää ellipsin, koska etäisyyksien summa pysyy vakiona.
Yhteenveto
- Ellipsi on käyrä, jonka pisteiden etäisyyksien summa kahdesta polttopisteestä on vakio (2a).
- Standardiyhtälö keskellä (h,k): ((x − h)²)/a² + ((y − k)²)/b² = 1.
- Polttopisteiden etäisyys keskipisteestä: c = √(a² − b²), eksentrisyys e = c/a.
- Pinta-ala A = π a b. Parametrinen esitys: x = h + a cos t, y = k + b sin t.
- Ellipsillä on hyödyllisiä fysiikan ja teknisten sovellusten ominaisuuksia, kuten reflektio- eli peilausominaisuus ja planeettojen kiertoratojen kuvaus.
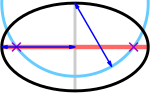
Polttopisteet (violetit ristit) ovat pääakselin (punainen) ja ympyrän (syaani) leikkauspisteissä, jonka säde on yhtä suuri kuin puolittainen pääakseli (sininen) ja jonka keskipiste on sivuakselin (harmaa) päässä.

Ellipsi, joka saadaan kartion ja tason leikkauspisteenä.
Ellipsi ja sen ominaisuudet.
Kysymyksiä ja vastauksia
Kysymys: Mikä on ellipsi?
V: Ellipsi on muoto, joka näyttää soikealta tai litistyneeltä ympyrältä. Geometriassa se on tasokäyrä, joka syntyy, kun kartio ja taso leikkaavat toisiaan siten, että syntyy suljettu käyrä.
K: Miten ellipsi luodaan?
V: Ellipsi voidaan tehdä laittamalla kaksi tappia pahviin ja vetämällä narua näiden kahden tapin ympärille, laittamalla kynä silmukkaan ja vetämällä niin pitkälle kuin mahdollista katkaisematta narua kaikkiin suuntiin.
K: Mitkä ovat ympyrän erityistapauksia?
V: Ympyrät ovat ellipsin erikoistapauksia, jotka syntyvät, kun leikkaustaso on kohtisuorassa kartion akselia vastaan.
K: Kuinka monta polttopistettä ellipsillä on?
V: Ellipsillä on kaksi polttopistettä.
K: Mikä yhtälö kuvaa ellipsin?
V: Ellipsin yhtälö on (x - h)²/a² + (y - k)²/b² = 1, jossa h ja k edustavat ellipsin keskipistettä ja 2a edustaa pituutta pidemmän laihemman sivun kummastakin päästä ja 2b edustaa pituutta lyhyemmän sivun kummastakin päästä. C edustaa sen polttopisteen ja keskipisteen välistä pituutta siten, että A²-B²=C².
Kysymys: Missä näemme esimerkkejä elliptisistä kiertoradoista?
V: Elliptisiä kiertoratoja voidaan nähdä planeetoissa, joiden aurinko on yhdessä polttopisteessä.
Etsiä
