Minkowskin avaruusaika — neljä ulottuvuutta erityisessä suhteellisuusteoriassa

Ymmärrä Minkowskin avaruusaika: neljä ulottuvuutta (kolme avaruus, yksi aika), (-+++) metriikka ja sen merkitys erityisessä suhteellisuusteoriassa.

Tekijä: Leandro Alegsa

Erityisessä suhteellisuusteoriassa Minkowskin avaruusaika on Hermann Minkowskin luoma neliulotteinen moniulotteinen avaruuus. Siinä on neljä ulottuvuutta: kolme avaruusulottuvuutta (x, y, z) ja yksi aikaulottuvuus. Minkowskin avaruusajan metriikka on (-+++), ja se kuvaa tasaista pintaa, kun massaa ei ole. Tässä artikkelissa Minkowskin avaruusaikaa kutsutaan yksinkertaisesti avaruusajaksi.

Minkowskin avaruusaikaa sovelletaan kuitenkin vain erityisessä suhteellisuusteoriassa. Yleisessä suhteellisuusteoriassa käytettiin kaarevaa avaruusaikaa kuvaamaan painovoiman ja kiihtyvän liikkeen vaikutuksia.

Peruskäsitteet

Minkowskin avaruusaika on geometrinen tapa esittää tapahtumia, joissa aikaa pidetään yhtenä ulottuvuutena muiden kolmen tilallisen ulottuvuuden rinnalla. Tapahtuma merkitään pisteenä avaruusajan nelidimensioisessa koordinaatistossa, esimerkiksi (ct, x, y, z) tai (t, x, y, z) jos asetetaan valonnopeus c = 1 yksiköissä.

Oma-aika (proper time) on kahden tapahtuman välillä liikkuvan kappaleen kokema aika. Se määritellään maailnalinjan (worldline) pitkin mitattuna intervallina, joka on invariantti eli sama kaikille inertiaalihavaitsijoille.

Metriikka ja invariantti intervalli

Minkowskin avaruajan alkeismitta (line element) ilmaistaan usein muodossa

ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2

tai vakiosta riippuen vaihtoehtoisella allekirjoituksella ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2. Tässä (-+++) tarkoittaa sitä, että aikakomponentti antaa negatiivisen termin ja avaruuskomponentit positiiviset; toista konventiota (+---) käytetään myös.

Intervalli ds^2 on invariantti Lorentz-muunnoksissa: eri inertiaalikoordinaatistot mittaavat saman arvon ds^2 kahden tietyn tapahtuman välillä. Intervallin merkki määrää, onko erottelu:

  • Timelike (ds^2 < 0): tapahtumat voivat olla syy-seuraussuhteessa; löytyy inertiaalihavaitsija jonka oma-aikana ne tapahtuvat samassa paikassa.
  • Lightlike / null (ds^2 = 0): tapahtumat yhdistyvät valonsäteellä; ne muodostavat valokartion (light cone).
  • Spacelike (ds^2 > 0): tapahtumat eivät voi olla kausaalisesti yhteydessä; eri havaitsijoilla voi olla erilainen järjestys simultaanisuuden suhteen.

Valokartio ja kausalisuus

Jokaisesta tapahtumasta piirretään avaruusaikaan valokartio, joka jakaa avaruusajan kolmeen osaan: tulevaan (inside future light cone), menneisyyteen (inside past light cone) ja muualla olevaan (outside the cones). Kausalisuus tarkoittaa, että vain tapahtumat, jotka sijaitsevat valokartion sisällä, voivat vaikuttaa toisiinsa syy-seuraussuhteessa.

Lorentz-muunnokset ja simultaanisuus

Lorentz-muunnokset yhdistävät eri inertiaalihavaitsijoiden koordinaatit siten, että ds^2 säilyy. Niiden seurauksena aika ja avaruus sekoittuvat: eri havaitsijat saattavat sopia yhtä tapahtumaa koskevasta ds^2:stä mutta eri t-arvoista. Tästä seuraa esimerkiksi aika-dilataatio ja pituussupistuma.

Nelivektorit ja fysiikan lauseet

Minkowskin avaruusaika tarjoaa luonnollisen kehyksen nelivektoreille (four-vectors), kuten aika-avaruuskoordinaatti (ct, x, y, z) ja neli-impulssi (E/c, p_x, p_y, p_z). Energiapito-impulssisuhde kirjoitetaan muotoon

E^2 = (pc)^2 + (mc^2)^2,

mikä seuraa metriikan invarianssista ja on helpommin ymmärrettävissä nelivektorien avulla.

Geometrinen näkökulma ja historia

Hermann Minkowski esitti vuonna 1908, että Einsteinille kehitetty erityinen suhteellisuusteoria saa elegantin geometrisen muodon näyttämällä ajan ja avaruuden yhtenä kokonaisuutena. Tämä geometrinen lähestymistapa yksinkertaistaa suhteellisuusteorian matemaattista muotoilua ja tekee näkyviksi ominaisuuksia kuten invariantin intervallin ja valokartion rakenteen.

Ero yleiseen suhteellisuusteoriaan

Erityinen suhteellisuusteoria ja Minkowskin avaruusaika pätevät tilanteissa, joissa gravitaatiovaikutukset voidaan jättää huomiotta: avaruusaika on tasainen (flat). Yleisessä suhteellisuusteoriassa avaruusaika on yleensä kaareva, ja sen kaarevuus kuvaa gravitaatiokenttiä. Kaarevassa avaruajassa metriikka riippuu paikasta ja energiasisällöstä, kun taas Minkowskin metriikka on globaali ja sama kaikissa pisteissä.

Käytännön havainnollistuksia

  • Minkowskin diagrammi on kaksiulotteinen piirros (tyypillisesti ct vs x), joka havainnollistaa valokartion, maailnalinjat ja samanaikaisuuden suhteellisuuden.
  • Oma-aika mitoittuu maailnalinjan pituutena Minkowskin metriikan mukaan; inertiaaliliikkeessä maailnalinja on suora.
  • Valonnopeuden asettaminen c = 1 helpottaa laskentaa ja tekee aikayksiköistä ja etäisyysyksiköistä yhteismitallisia.

Yhteenveto

Minkowskin avaruusaika on keskeinen käsite erityisessä suhteellisuusteoriassa: se yhdistää ajan ja avaruuden nelidimensionaaliseksi geometriseksi rakenteeksi, jossa invariantti intervalli ja valokartion muoto määräävät kausaalisen järjestyksen. Se tarjoaa luonnollisen kehyksen nelivektoreille ja tekee Lorentz-invariantit ilmiöt, kuten aika-dilataation ja energian ja impulssin väliset yhteydet, helposti ymmärrettäviksi. Kun gravitaatio otetaan huomioon, siirrytään yleisen suhteellisuusteorian kaarevaan avaru-aikaan.

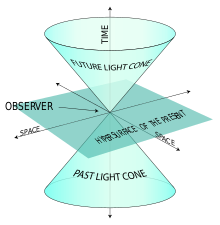
Esimerkki valokartiosta.  Zoom
Esimerkki valokartiosta.  

Määritelmä(t)

Matemaattinen

Avaruusaikaa voidaan ajatella neliulotteisena koordinaatistona, jonka akselit ovat seuraavat

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)}

Niitä voidaan merkitä myös seuraavasti

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} {\displaystyle (x_{1},x_{2},x_{3},x_{4})}

Jossa x 1 {\displaystyle x_{1}}{\displaystyle x_{1}} edustaa c t {\displaystyle ct}{\displaystyle ct} . Aika mitataan valonnopeuden ja aikakoordinaatin kerrannaisina, koska ajan yksiköt ovat samat kuin avaruuden yksiköt. Avaruusajan kaaren pituuden differentiaali on seuraava

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}

Tämä tarkoittaa, että avaruusajalla on metrinen tensori, joka saadaan seuraavalla kaavalla

g u v = [ - 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&0&1\end{bmatrix}}} {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}}

Kuten edellä todettiin, avaruusaika on kaikkialla litteää; jossain määrin sitä voidaan ajatella tasona.

Yksinkertainen

Avaruusaikaa voidaan pitää "areenana", jolla kaikki maailmankaikkeuden tapahtumat tapahtuvat. Avaruusajan pisteen määrittämiseksi tarvitaan vain tietty aika ja tyypillinen avaruudellinen suunta. Neljää ulottuvuutta on vaikea (käytännössä mahdotonta) visualisoida, mutta jonkinlainen analogia voidaan tehdä käyttämällä seuraavaa menetelmää.



 

Avaruusajan kaaviot

Hermann Minkowski esitteli tietyn menetelmän koordinaatistojen kuvaajien kuvaamiseen Minkowskin avaruusajassa. Kuten oikealla näkyy, eri koordinaattijärjestelmät ovat eri mieltä kohteen avaruudellisesta orientaatiosta ja/tai ajallisesta sijainnista. Kuten kaaviosta näkyy, on vain yksi avaruudellinen akseli (x-akseli) ja yksi aika-akseli (ct-akseli). Tarvittaessa voidaan ottaa käyttöön ylimääräinen avaruudellinen ulottuvuus (y-akseli); valitettavasti tämä on ulottuvuuksien määrän raja: kuvaajien esittäminen neljässä ulottuvuudessa on mahdotonta. Minkowskin avaruusajan kuvaajaa koskeva sääntö on seuraava:

1) x-akselin ja x'-akselin välinen kulma saadaan kaavalla t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}}{\displaystyle tan(\alpha )={\frac {v}{c}}} missä v on kappaleen nopeus.

2) Valon nopeus avaruusajan läpi muodostaa aina 45 asteen kulman jommankumman akselin kanssa.



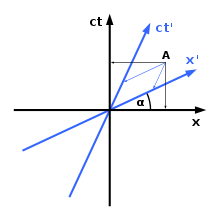
 Suhteellisuusteoriassa molemmat havaitsijat ajoittavat tapahtuman A eri ajankohtiin.  Zoom
Suhteellisuusteoriassa molemmat havaitsijat ajoittavat tapahtuman A eri ajankohtiin.  

Avaruusaika yleisessä suhteellisuusteoriassa

Einstein käytti yleisessä suhteellisuusteoriassaan yhtälöä

G m v = 8 π G T m v {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T}\mathbb {T} _{mv}} {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}}

Jotta avaruusaika todella kaartuisi; tästä aiheutuvat vaikutukset ovat gravitaation vaikutuksia.



 

Aiheeseen liittyvät sivut

Viranomaisvalvonta: Kansalliskirjastot Edit this at Wikidata
  • Ranska (tiedot)
  • Saksa
  • Yhdysvallat
  • Latvia
  • Tšekin tasavalta


 

Kysymyksiä ja vastauksia

K: Mitä on Minkowskin avaruusaika?


V: Minkowskin avaruusaika on Hermann Minkowskin luoma neliulotteinen moninaisuus. Siinä on kolme avaruusulottuvuutta (x, y, z) ja yksi aikaulottuvuus.

K: Mikä on Minkowskin avaruusajan metriikka?


V: Minkowskin avaruusajan metriikka on (-+++).

K: Miten Minkowskin avaruusaika kuvaa tasaista pintaa?


V: Kun massaa ei ole, Minkowskin avaruusaika kuvaa tasaista pintaa.

K: Sovelletaanko Minkowskin avaruusaikaa yleiseen suhteellisuusteoriaan?


V: Ei, Minkowskin avaruusaikaa sovelletaan vain erityisessä suhteellisuusteoriassa. Yleisessä suhteellisuusteoriassa käytetään kaarevaa avaruusaikaa kuvaamaan painovoiman ja kiihtyvän liikkeen vaikutuksia.

K: Kuinka monta ulottuvuutta Minkowskin avaruusajalla on?


V: Minkowsin avaruusajassa on neljä ulottuvuutta - kolme avaruusulottuvuutta (x, y, z) ja yksi aikaulottuvuus.

K: Kuka loi Minkowsin avaruusajan käsitteen?


V: Hermann Minkowksi loi MInkowskin avaruusajan käsitteen.


Etsiä
AlegsaOnline.com - 2020 / 2025 - License CC3