Aika-avaruus (Minkowski): neljäulotteinen jatkumo ja relativiteetti
Tutustu Minkowskin neljäulotteiseen aika-avaruuteen ja relativiteettiin: miten nopeus ja gravitaatio muokkaavat ajan kulun ja avaruuden suhteita.
Avaruusaika on matemaattinen malli, joka yhdistää avaruuden ja ajan yhdeksi ajatukseksi, jota kutsutaan jatkumoksi. Tämä neliulotteinen jatkumo tunnetaan nimellä Minkowskin avaruus.
Näiden kahden ajatuksen yhdistäminen auttoi kosmologiaa ymmärtämään, miten maailmankaikkeus toimii suurella tasolla (esim. galaksit) ja pienellä tasolla (esim. atomit).
Euklidisen avaruuden käyttö ei-relativistisessa klassisessa mekaniikassa aika-avaruuden sijasta on hyvä, koska aikaa käsitellään universaalina, jonka kulumisnopeus on vakio ja joka on riippumaton havaitsijan liiketilasta.
Relativistisessa maailmankaikkeudessa aikaa ei kuitenkaan voida erottaa avaruuden kolmesta ulottuvuudesta. Tämä johtuu siitä, että havaittu ajan kulumisnopeus riippuu kohteen nopeudesta suhteessa havaitsijaan. Lisäksi minkä tahansa gravitaatiokentän voimakkuus hidastaa kentän ulkopuolisen havaitsijan näkemän kohteen ajan kulumista.
Peruskäsitteet ja matemaattinen kuvaus
Minkowskin avaruus on neljäulotteinen taso, jossa aika yhdistyy kolmeen avaruusulottuvuuteen. Käytännössä piste tällä jatkumolla (ns. tapahtuma) merkitään koordinaateilla (t,x,y,z). Aika ja avaruus yhdistyvät niin, että niiden välinen etäisyys mitataan aikavälillä eli invariantilla intervalilla.
- Invariantti aikaväli s^2 on kaavan muotoinen (yksinkertaistaen käyttäen SI-yksiköitä):
s^2 = -c^2 (Δt)^2 + (Δx)^2 + (Δy)^2 + (Δz)^2,
jossa c on valonnopeus. Usein käytetään yksiköitä, joissa c = 1, jolloin hieman yksinkertaisempi esitys riittää. - Riippuen s^2:n merkistä erotetaan kolme tyyppiä: timelike (s^2 < 0), spacelike (s^2 > 0) ja lightlike eli valonkaltainen (s^2 = 0). Nämä määräävät, voiko kaksi tapahtumaa olla syy-seuraussuhteessa (causal) vai eivät.
- Lorentz-muunnokset ovat ne koordinaattimuunnokset, jotka säilyttävät intervalin arvon. Ne korvaavat klassisen Galilein muunnoksen relativistisessa kehyksessä.
Geometrinen kuva: valonkehä ja maailmaviivat
Ajatus on helpompi hahmottaa piirroksissa (aikadiagrammit): tapahtuma ympärillä oleva valonkehä (light cone) erottaa ne tapahtumat, joihin voidaan vaikuttaa tai joista voidaan saada vaikutus (sisäinen keko) niistä, jotka ovat yhteydessä vain epäonnistuvasti (ulkoinen alue).
Jokaisen kappaleen liike aika-avaruudessa on maailmaviiva (worldline). Lepo- tai inertiaalisen liikkeen tapauksessa maailmaviiva on suora linja Minkowskin avaruudessa; kiihtyvä liike tai gravitaation vaikutus näkyy viivan kaareutena (yleisessä suhteellisuusteoriassa kaareutena avaruuden ja ajan kokonaisuudessa).
Seuraukset ja havainnollistaminen
- Ajan laajeneminen (time dilation): liikkuvalle kappaleelle mitattu oma aika (proper time) kuluu hitaammin suhteessa liikkeeseen nähden lepäävään havaitsijaan. Tämä on suoraan seuraus Lorentz-muunnoksista ja invariantista intervalista.
- Pituuden supistuminen (length contraction): liikkuvien kappaleiden mitattu pituus kappaleen liikennesuunnassa lyhenee suhteessa lepäävän havaitsijan mittaukseen.
- Samanaikaisuuden relativisuus: kaksi tapahtumaa, jotka ovat samanaikaisia yhdessä inertiaalikehyksessä, eivät välttämättä ole samanaikaisia toisessa kehyksessä.
Minkowski vs. Euklidinen geometria ja yleinen suhteellisuusteoria
Euklidinen geometria kuvaa kolmiulotteista tilaa, jossa mitta- ja kulmasuhteet ovat klassisia. Minkowskin avaruudessa käytetään erilaista metriikkaa (ei-euklidinen signatuuri), mikä heijastuu edellä mainittuun minusmerkkiseen ajanosaan kaavassa. Tämä ero on syy siihen, miksi aika ja avaruus eivät ole yksinkertaisesti samoja ulottuvuuksia kuin lisätilat.
Erityinen suhteellisuusteoria kuvaa fysiikkaa Minkowskin tasaisessa (flättissä) aika-avaruudessa, kun taas yleinen suhteellisuusteoria yleistää tämän kuvaamalla gravitaation ajan- ja avaruuden kaareutumisena. Gravitaatiokenttä ei siis ole voima klassisessa merkityksessä, vaan seuraus aika-avaruuden geometriasta.
Käytännön merkitys
Minkowskin aika-avaruus ei ole pelkkä abstraktio: sen ennusteita on mitattu ja hyödynnetty käytännössä. Esimerkkejä:
- GPS-satelliittien kellot toimivat oikein vain ottamalla huomioon sekä suhteellisuusteorian erikois- että yleisvaikutukset.
- Hiukkaskiihdyttimissä aika-avaruuden relativistiset vaikutukset näyttelevät keskeistä roolia hiukkasten eliniän ja hajoamisten mittauksissa.
- Kosmologisissa malleissa avaruusaika muodostaa pohjan maailmankaikkeuden laajenemista ja gravitaatiovaikutuksia kuvaaville teorioille.
Yhteenveto: Minkowskin avaruus yhdistää ajan ja avaruuden geometriseksi jatkumoksi, jossa invariantti aikaväli ja Lorentz-symmetria määrittelevät, mitä tapahtuu eri havaitsijoiden välillä. Tämä geometrinen näkemys selittää ajan laajenemisen, pituuden supistumisen ja samanaikaisuuden relativisuuden sekä toimii lähtökohtana yleiselle suhteellisuusteorialle, jossa gravitaatio ilmenee aika-avaruuden kaareutumisena.
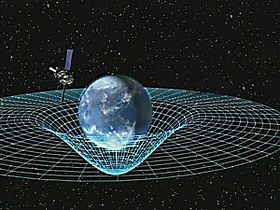
Havainnollistus Maan aiheuttamasta aika-avaruuden kaarevuudesta.
Muita näkökohtia
Missä tahansa materiaa on olemassa, se taivuttaa avaruusajan geometriaa. Tämä johtaa aika-avaruuden kaarevaan muotoon, joka voidaan ymmärtää painovoimana. Oikeanpuoleisen kuvan valkoiset viivat kuvaavat massan vaikutusta aika-avaruuteen.
Klassisessa mekaniikassa avaruusajan käyttö on vapaaehtoista, koska aika on riippumaton liikkeestä euklidisen avaruuden kolmessa ulottuvuudessa. Kun kappale kuitenkin liikkuu lähes valonnopeudella (relativistisilla nopeuksilla), aikaa ei voida erottaa avaruuden kolmesta ulottuvuudesta. Paikallaan olevan tarkkailijan näkökulmasta aika riippuu siitä, kuinka lähellä valonnopeutta kappale liikkuu.
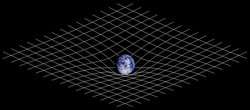
Kaksiulotteinen analogia aika-avaruuden vääristymästä
Historiallinen alkuperä
Monet yhdistävät avaruusajan Albert Einsteiniin, joka esitti vuonna 1905 erityisen suhteellisuusteorian. Einsteinin opettaja Hermann Minkowski ehdotti kuitenkin avaruusaikaa vuonna 1908 julkaistussa esseessään. Hänen Minkowskin avaruuskäsitteensä on varhaisin tapa käsitellä avaruutta ja aikaa yhtenäisen kokonaisuuden kahtena osana, mikä on erityisen suhteellisuusteorian ydin. Hän toivoi, että tämä uusi ajatus selkeyttäisi erityistä suhteellisuusteoriaa.
Minkowskin avaruusaika kuvaa tarkasti vain vakionopeutta. Einstein oli kuitenkin se, joka löysi aika-avaruuden kaarevuuden (gravitaation) yleisessä suhteellisuusteoriassa. Yleisessä suhteellisuusteoriassa Einstein yleisti Minkowskin aika-avaruuden siten, että se sisältää kiihtyvyyden vaikutukset. Einstein havaitsi, että hänen neliulotteisen aika-avaruusesityksensä kaarevuus oli itse asiassa painovoiman syy.
Vuonna 1926 julkaistussa Encyclopedia Britannican kolmannessatoista painoksessa oli Einsteinin artikkeli "space-time".
Kirjallinen tausta
Edgar Allan Poe kirjoitti kosmologiaa käsittelevän esseen Eureka (1848), jonka mukaan "avaruus ja kesto ovat yhtä". Tämä on ensimmäinen tunnettu tapaus, jossa avaruus ja aika on todettu yhden asian eri käsityksiksi. Poe päätyi tähän johtopäätökseen noin 90 sivua kestäneiden perustelujen jälkeen, mutta hän ei käyttänyt matematiikkaa.
Vuonna 1895 H.G. Wells kirjoitti romaanissaan Aikakone: "Ajan ja minkään avaruuden kolmen ulottuvuuden välillä ei ole muuta eroa kuin se, että tietoisuutemme liikkuu sitä pitkin". Hän lisäsi: "Tieteilijät... tietävät hyvin, että aika on vain eräänlainen avaruus".
Avaruusaika kvanttimekaniikassa
Yleisessä suhteellisuusteoriassa avaruusajan ajatellaan olevan sileää ja jatkuvaa. Kvanttimekaniikan teoriassa avaruusaika ei kuitenkaan ole aina jatkuvaa.
Aiheeseen liittyvät sivut
- Mitta
- Jakelukanava
Kysymyksiä ja vastauksia
K: Mitä on avaruusaika tekstin mukaan?
A: Avaruusaika on matemaattinen malli, joka yhdistää avaruuden ja ajan muodostaen neliulotteisen jatkumon, joka tunnetaan nimellä Minkowskin avaruus.
K: Miten avaruuden ja ajan yhdistäminen on auttanut kosmologiaa?
V: Avaruuden ja ajan yhdistäminen on antanut kosmologialle mahdollisuuden ymmärtää paremmin, miten maailmankaikkeus toimii sekä suurella tasolla, kuten galakseissa, että pienellä tasolla, kuten atomeissa.
K: Miksi euklidisen avaruuden käyttö aika-avaruuden sijasta on hyvä ei-relativistisessa klassisessa mekaniikassa?
V: Euklidisen avaruuden käyttö ei-relativistisessa klassisessa mekaniikassa on hyvä, koska aikaa käsitellään universaalina, jonka kulumisnopeus on vakio ja joka on riippumaton havaitsijan liiketilasta.
Kysymys: Miksi aika on erottamaton kolmesta avaruuden ulottuvuudesta relativistisessa maailmankaikkeudessa?
V: Aikaa ei voi erottaa kolmesta avaruuden ulottuvuudesta relativistisessa maailmankaikkeudessa, koska havaittu ajan kulumisnopeus riippuu kohteen nopeudesta suhteessa havaitsijaan.
K: Miten gravitaatiokentän voimakkuus vaikuttaa kappaleen ajan kulumiseen?
V: Minkä tahansa gravitaatiokentän voimakkuus hidastaa kentän ulkopuolisen havaitsijan näkemän kappaleen ajan kulumista.
K: Mikä on sen neliulotteisen jatkumon nimi, joka yhdistää avaruuden ja ajan?
V: Avaruuden ja ajan yhdistävää neliulotteista jatkumoa kutsutaan Minkowskin avaruudeksi.
K: Miten avaruuden ja ajan yhdistäminen on auttanut kosmologiaa ymmärtämään maailmankaikkeutta?
V: Avaruuden ja ajan yhdistelmä on auttanut kosmologiaa ymmärtämään paremmin maailmankaikkeuden toimintaa sekä suurella tasolla, kuten galakseissa, että pienellä tasolla, kuten atomeissa.
Etsiä