Nomogrammi (abaque) – graafinen laskukaavio: määritelmä ja käyttö
Tutustu nomogrammiin (abaque): graafinen laskukaavio, sen historia, rinnakkaiskoordinaatit ja käytännön käyttö insinööreille nopeisiin laskutoimituksiin.
Nomogrammi (myös yhdenmukaistamiskaavio tai abaque) on grafiikkaan perustuva laskentakaavio. Se on kaksiulotteinen esitys, jossa matemaattisen suhteen tai funktion laskutoimitus voidaan ratkaista visuaalisesti ilman algebrallista laskemista. Nomogrammeissa esitetään yleensä useita asteikkoja, joista yksi vastaa yhtälön kutakin muuttujaa. Kun tunnetaan n−1 muuttujan arvot, tuntemattoman muuttujan arvo voidaan löytää asettamalla esimerkiksi viivoitin tai suorakulmaisen viivan kaltainen apuviiva tunnettuja arvoja yhdistävien asteikkojen yli.
Nomografian perusajatus kehitettiin ja vakiinnutettiin vuonna 1884 ranskalaisen insinöörin Philbert Maurice d'Ocagnen (1862–1938) toimesta. Nomogrammeissa käytetään d'Ocagnen kehittämää rinnakkaiskoordinaattijärjestelmää tavanomaisten kartesiokoordinaattien sijasta. Nomogrammit olivat erityisen suosittuja 1900-luvun alku- ja keskivaiheilla, kun graafinen laskenta tarjosi nopean, kenttäoloihin soveltuvan vaihtoehdon laskimille ja tietokoneille.
Miten nomogrammi toimii
Nomogrammi koostuu useista asteikoista, joista kukin vastaa yhtä muuttujaa. Asteikot voivat olla suoria, kaarevia tai logaritmisia riippuen tarvittavasta muunnoksesta. Kun tunnetaan n−1 muuttujan arvot, asetetaan viivoitin tunnettuja pisteitä yhdistävien asteikkojen yli. Piste, jossa viivoitin leikkaa tuntemattoman muuttujan asteikon, antaa halutun arvon. Tämä virtuaalista tai piirrettyä viivaa kutsutaan indeksiviivaksi tai isopletiksi.
Tyypillisiä nomogrammityyppejä
- Yksinkertainen lineaarinen nomogrammi: Kolme suoraa asteikkoa, joista kaksi tunnetaan ja kolmas lasketaan suoraviivaisesti.
- Logaritminen nomogrammi: Käytetään monikertolaskujen ja potenssien esittämiseen; log-asteikot muuttavat kertolaskun yhteenlaskuksi.
- Kaarevat tai muotoillut asteikot: Kun muuttujien välinen riippuvuus ei muunnu suoraviivaisesti, käytetään käyriä asteikkoja tai erikoismuotoja.
- Ristikko- või verkko-nomogrammit: Monimuuttujaiset ongelmat voidaan esittää ruudukkomaisesti tai konstruoida monimutkaisempia relaatioita varten.
- Pyörivät (circular) nomogrammit: Asteikot sijoitetaan kehälle; hyödyllisiä toistuviin laskuesityksiin ja pienissä mittakaavoissa.
Esimerkkejä käytöstä
- Tekninen laskenta: putkisto- ja virtauslaskelmat, painehäviöt, Manningin kaava.
- Sähkötekniikka: Ohmin lain, jännitteen, virran ja resistanssin väliset suhteet.
- Lääketiede: kehon pinta-alan (BSA), annostuslaskelmien ja riskiluokitusten nopeasti arviointi.
- Ilmailu ja navigointi: polttoaineen kulutus, matkanopeus ja etäisyydet.
- Geologia ja metsätalous: puuston arviointi, maa-ainesten ominaisuudet.
Nomogrammin rakentaminen (perusvaiheet)
- Valitse yhtälö tai relaatio ja määritä muuttujat.
- Tarvittaessa tee muunnoksia (esim. logaritmi- tai käänteisfunktio), jotta suhde voidaan esittää asteikoilla lineaarisena.
- Päätä asteikkojen järjestys ja skaala (lineaarinen, logaritminen, taite-asteikko).
- Piirrä asteikot tarkkuusvaatimusten mukaisesti ja merkitse mittayksiköt.
- Kalibroi nomogrammi laskemalla useita tunnettuja tapauksia ja merkitsemällä tulokset asteikoille.
Edut ja rajoitukset
- Edut: Nopea visuaalinen ratkaisu ilman laskinta tai tietokonetta; helppo käyttää kenttäoloissa; intuitiivinen esitys ja hyvä oppimisväline käsitteellistämään muuttujien välisiä suhteita.
- Rajoitukset: Tarkkuus riippuu asteikkojen resoluutiosta ja käyttäjän kyvystä asettaa viivoitin tarkasti; vaikea saavuttaa hyvin suurta numeerista tarkkuutta; monimutkaisemmat funktiot vaativat erikoisasteikkoja ja suunnittelua.
Nykykäyttö ja ohjelmistot
Vaikka elektroniset laskimet ja tietokoneohjelmistot ovat syrjäyttäneet nomogrammien laajan käytön, niitä käytetään edelleen opetuksessa, nopeissa kenttäarvioissa ja tilanteissa, joissa visuaalinen tulkinta on hyödyllinen. Nomogrammeja voi nykyään luoda myös tietokoneella: on olemassa erilaisia ohjelmia ja kirjastoja, jotka piirtävät nomogrammeja automaattisesti (esim. R- ja Python-ympäristöissä olevat työkalut).
Käyttövinkkejä
- Piirrä asteikot riittävän pitkinä ja merkitse väliotsikot selkeästi, jotta lukeminen on helppoa.
- Käytä viivainta tai suoraa reunaa täsmällisten lukemien saamiseksi.
- Merkkaa testitapaukset nomogrammiin varmistaaksesi rakenteen oikeellisuuden ja herkkyyden eri arvoalueilla.
Nomogrammi on käytännöllinen työkalu nopeaan, visuaaliseen laskemiseen ja havainnollistamiseen. Se yhdistää matemaattisen funktion ja inhimillisen lukutavan tavalla, joka on ollut käyttökelpoinen ennen digitaalisten laskimien aikaa ja säilyttää paikkansa opetuksessa ja tietyissä käytännön sovelluksissa.
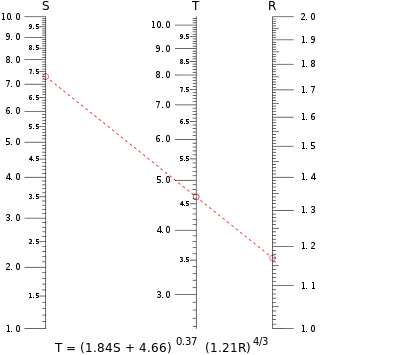
Tyypillinen rinnakkaisasteikollinen nomogrammi. Tässä esimerkissä lasketaan T:n arvo, kun S = 7,30 ja R = 1,17 korvataan yhtälössä. Isopletti ylittää T:n asteikon hieman alle 4,65:n kohdalla.
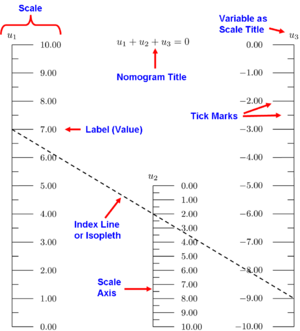
Rinnakkaisasteikollisen nomogrammin osat
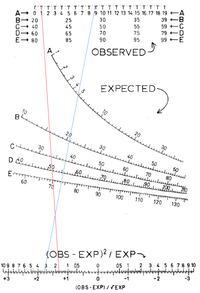
Khiin neliöjakauman nomogrammi
Käytä
Nomogrammeja käytettiin laajalti noin 75 vuoden ajan. Ne mahdollistivat nopeat ja tarkat laskutoimitukset ennen taskulaskinten aikakautta. Nomogrammin tulokset saadaan nopeasti ja luotettavasti piirtämällä yksi tai useampi viiva. Käyttäjän ei tarvitse osata ratkaista algebrallisia yhtälöitä, etsiä tietoja taulukoista, käyttää laskutikkua tai korvata numeroita yhtälöihin saadakseen tuloksia. Käyttäjän ei tarvitse edes tietää, mitä yhtälöä nomogrammi edustaa.
Nomogrammien suunnittelussa on käytetty toimialatietoa. Esimerkiksi suurempien nomogrammien luomiseksi ja suuremman tarkkuuden saavuttamiseksi nomografi sisällyttää yleensä vain sellaiset asteikkoalueet, jotka ovat järkeviä ja jotka ovat ongelman kannalta kiinnostavia. Monet nomogrammit sisältävät myös muita hyödyllisiä merkintöjä, kuten vertailumerkintöjä ja värillisiä alueita. Kaikki nämä tarjoavat käyttäjälle hyödyllisiä opasteita.
Kuten laskutikku, nomogrammi on graafinen analoginen laskentalaite. Laskutason tavoin sen tarkkuutta rajoittaa tarkkuus, jolla fyysiset merkinnät voidaan piirtää, toistaa, tarkastella ja kohdistaa.Laskutason laskutoimitus on yleiskäyttöinen laskin, mutta nomogrammi on suunniteltu suorittamaan tietty laskutoimitus. Nomogrammeja voidaan silti käyttää tarkistamaan toisen, tarkemman mutta mahdollisesti virhealttiimman laskutoimituksen antama vastaus.
Kysymyksiä ja vastauksia
K: Mikä on nomogrammi?
A: Nomogrammi on laskennassa käytettävä kuvaaja, joka antaa laskennan matemaattisesta funktiosta.
K: Kuka keksi nomografian alan?
A: Nomografian keksi ranskalainen insinööri Philbert Maurice d'Ocagne vuonna 1884.
K: Mikä oli nomogrammien tarkoitus?
V: Nomogrammeja käytettiin monta vuotta, jotta insinöörit saisivat nopeasti graafisia laskutoimituksia monimutkaisista kaavoista.
K: Kuinka monesta asteikosta nomogrammi koostuu?
V: Nomogrammi koostuu n asteikosta, joista yksi on kullekin yhtälön muuttujalle.
K: Miten tuntemattoman muuttujan arvo voidaan löytää nomogrammin avulla?
V: Kun tiedetään n-1 muuttujan arvot, tuntemattoman muuttujan arvo voidaan löytää asettamalla viivoitin asteikolla olevien tunnettujen arvojen poikki ja lukemalla tuntematon arvo siitä kohdasta, jossa se ylittää kyseisen muuttujan asteikon.
K: Mikä on viivoittimen luoman virtuaalisen tai piirretyn viivan nimi?
V: Suorakulmion luomaa virtuaalista tai piirrettyä viivaa kutsutaan indeksiviivaksi tai isopletiksi.
K: Minkälaista koordinaattijärjestelmää käytetään nomogrammeissa?
V: Nomogrammeissa käytetään d'Ocagnen keksimää rinnakkaiskoordinaattijärjestelmää tavanomaisten kartesiokoordinaattien sijasta.
Etsiä