Laskutikku | mekaaninen analoginen tietokone

Peruskäsitteet

Perusmuodossaan laskutikku käyttää kahta logaritmista asteikkoa, joiden avulla lukujen kertominen ja jakaminen on nopeaa. Nämä yleiset operaatiot voivat olla aikaa vieviä ja virhealttiita, kun ne tehdään paperilla. Monimutkaisemmat laskutikut mahdollistavat muut laskutoimitukset, kuten neliöjuuret, eksponentit, logaritmit ja trigonometriset funktiot.

Matemaattiset laskutoimitukset tehdään kohdistamalla liukuvassa keskiliuskassa oleva merkki johonkin kiinteässä liuskassa olevaan merkkiin. Tämän jälkeen voidaan tarkkailla muiden merkkien suhteellista sijaintia. Merkkien kanssa samassa linjassa olevat numerot antavat tuotteen, kertolaskun tai muun lasketun tuloksen likiarvon.

Käyttäjä määrittää desimaalipisteen sijainnin tuloksessa henkisen arvion perusteella. Tieteellistä merkintätapaa käytetään desimaalipisteen jäljittämiseen virallisemmissa laskutoimituksissa. Laskutoimitusten yhteen- ja vähennyslaskuvaiheet tehdään yleensä henkisesti tai paperilla, ei laskutikulla.

Useimmissa liukusäätimissä on kolme samanpituista lineaariliuskaa. Liuskat on kohdistettu rinnakkain ja lukittu toisiinsa siten, että keskimmäistä liuskaa voidaan siirtää pituussuunnassa kahteen muuhun liuskaan nähden. Kaksi ulompaa liuskaa on kiinnitetty siten, että niiden suhteellinen sijainti ei muutu.

Joissakin liukusäännöissä ("duplex"-malleissa) on asteikot sekä säännön että liukuliuskan molemmilla puolilla, toisissa liukuliuskojen toisella puolella ja liukuliuskan molemmilla puolilla ja taas toisissa vain toisella puolella ("simplex"-säännöt). Pystysuoralla kohdistusviivalla varustettua liukukursoria käytetään sellaisten asteikkojen vastaavien pisteiden etsimiseen, jotka eivät ole vierekkäin tai jotka duplex-malleissa ovat säännön toisella puolella. Kursori voi myös tallentaa välituloksen millä tahansa asteikolla.

 
Kursori liukusäätimellä  

Laskutoimitusten tekeminen laskutoimituksella

Kertolasku

Logaritmi muuttaa kerto- ja jako-operaatiot yhteen- ja vähennyslaskuiksi sääntöjen log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} ja log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} mukaisesti. Kun yläasteikkoa siirretään oikealle log ( x ) {\displaystyle \log(x)} verran, sovittamalla yläasteikon alku alhaalla olevaan merkintään x {\displaystyle x} , jokainen luku y {\displaystyle y} kohdistetaan oikealle. , joka on yläasteikon kohdassa log ( y ) {\displaystyle \log(y)} , numeron kanssa, joka on ala-asteikon kohdassa log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} . Koska log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} , tämä sijainti ala-asteikolla antaa x y {\displaystyle xy} , x {\displaystyle x} ja y {\displaystyle y} tulo. Esimerkiksi laskettaessa 3 × 2 (laskimessa 3*2), yläasteikon 1 siirretään ala-asteikon 2:n kohdalle. Vastaus, 6, luetaan ala-asteikolta, kun 3 on yläasteikolla. Yleisesti ottaen yläasteikon 1 siirretään ala-asteikon kertoimen kohdalle, ja vastaus luetaan ala-asteikolta, jossa toinen kerroin on yläasteikolla.

Operaatiot voivat mennä "asteikon ulkopuolelle"; esimerkiksi yllä olevassa kaaviossa näkyy, että liukusääntö ei ole asettanut ylemmän asteikon 7:ää minkään alemman asteikon luvun yläpuolelle, joten se ei anna vastausta 2×7:ään. Tällaisissa tapauksissa käyttäjä voi liu'uttaa ylempää asteikkoa vasemmalle, kunnes sen oikeanpuoleinen indeksi on 2:n kohdalla, ja näin kerrotaan 0,2:lla eikä 2:lla, kuten alla olevassa kuvassa:

Tässä tapauksessa laskutikun käyttäjän on muistettava säätää desimaalipilkku asianmukaisesti lopullisen vastauksen korjaamiseksi. Halusimme löytää 2×7, mutta sen sijaan laskimme 0,2×7=1,4. Oikea vastaus ei siis ole 1,4 vaan 14. Diaattorin nollaaminen ei ole ainoa tapa käsitellä kertolaskuja, jotka johtaisivat asteikon ulkopuolisiin tuloksiin, kuten 2×7; joitakin muitakin menetelmiä on olemassa:

• (1) Käytä kahden vuosikymmenen asteikkoja A ja B.
• (2) Käytä taitettuja asteikkoja. Tässä esimerkissä aseta C:n vasen 1 vastakkain D:n 2:n kanssa. Siirrä kursori CF:n kohtaan 7 ja lue tulos DF:stä.
• (3) Käytä käänteistä CI-asteikkoa. Aseta CI-asteikon piste 7 D-asteikon pisteen 2 yläpuolelle ja lue tulos D-asteikolta CI-asteikon pisteen 1 alapuolelta. Koska 1 esiintyy kahdessa paikassa CI-asteikolla, toinen niistä on aina asteikolla.
• (4) Käytä sekä käänteistä CI-asteikkoa että C-asteikkoa. Kohdista CI:n 2 D:n 1:een ja lue tulos D:stä C-asteikon 7:n alapuolelta.

Menetelmä 1 on helppo ymmärtää, mutta se aiheuttaa tarkkuuden menetyksen. Menetelmän 3 etuna on, että siinä käytetään vain kahta asteikkoa.

Osasto

Alla olevassa kuvassa on esitetty laskutoimitus 5,5/2. Yläasteikon 2 on sijoitettu ala-asteikon 5,5:n päälle. Yläasteikolla oleva 1 on 2,75:n yläpuolella. Jaon tekemiseen on olemassa useampiakin menetelmiä, mutta tässä esitetyn menetelmän etuna on, että lopputulos ei voi olla asteikon ulkopuolella, koska voidaan valita, käytetäänkö 1:tä jommassakummassa päässä.

Muut toiminnot

Joissakin laskutoimituksissa on logaritmiskaalojen lisäksi muita matemaattisia toimintoja, jotka on koodattu muille apuasteikoille. Suosituimpia olivat trigonometriset asteikot, yleensä sini ja tangentti, yhteinen logaritmi (log10) (kertojan asteikolla olevan arvon logaritmin ottamiseksi), luonnollinen logaritmi (ln) ja eksponentiaalinen asteikko (e^x ). Joihinkin sääntöihin kuuluu myös Pythagoraan asteikko, jolla voidaan laskea kolmioiden sivuja, ja asteikko, jolla voidaan laskea ympyröitä. Toisissa säännöissä on asteikot hyperbolisten funktioiden laskemista varten. Lineaarisissa säännöissä asteikot ja niiden merkinnät ovat hyvin standardoituja, ja vaihtelua esiintyy yleensä vain siinä, mitkä asteikot ovat mukana ja missä järjestyksessä:

A, B	kahden desimaalin logaritmiset asteikot, joita käytetään lukujen neliöjuurten ja neliöiden löytämiseen.
C, D	yhden vuosikymmenen logaritmiset asteikot
K	kolmen desimaalin logaritminen asteikko, jota käytetään lukujen kuutiojuurien ja kuutioiden löytämiseen.
CF, DF	C- ja D-asteikkojen "taitetut" versiot, jotka alkavat π:stä eikä ykkösestä; nämä ovat käteviä kahdessa tapauksessa. Ensinnäkin, kun käyttäjä arvelee tuotteen olevan lähellä 10:tä, mutta ei ole varma, onko se hieman alle vai hieman yli 10, taitetut asteikot välttävät mahdollisuuden poiketa asteikosta. Toiseksi, kun alkuarvo on π eikä 10:n neliöjuuri, kertominen tai jakaminen π:llä (mikä on yleistä luonnontieteellisissä ja teknisissä kaavoissa) yksinkertaistuu.
CI, DI, DIF	"käänteiset" asteikot, jotka kulkevat oikealta vasemmalle ja joita käytetään 1/x-askeleiden yksinkertaistamiseen.
S	jota käytetään sinien ja kosinusten määrittämiseen D-asteikolla.
T	jota käytetään tangenttien ja kolmiulotteisten pisteiden löytämiseen D- ja DI-asteikoilla.
ST, SRT	käytetään pienten kulmien sinien ja tangenttien sekä asteen ja radiaanin muuntamiseen.
L	lineaarinen asteikko, jota käytetään yhdessä C- ja D-asteikkojen kanssa 10-kantaisten logaritmien ja 10:n potenssien löytämiseen.
LLn	joukko log-log-asteikkoja, joita käytetään lukujen logaritmien ja eksponentiaalien löytämiseen.
Ln	lineaarinen asteikko, jota käytetään yhdessä C- ja D-asteikkojen kanssa luonnollisten logaritmien (perusta e) ja e x {\displaystyle e^{x}}

 

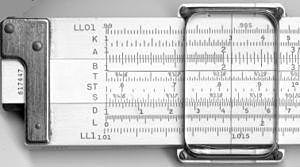
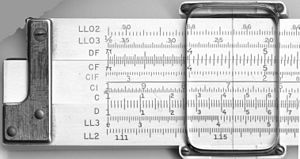
K&E 4081-3 -liukusäätimen etu- ja takaosan asteikot.

Gilsonin vuonna 1931 valmistama binäärinen liukusääntö suoritti yhteen- ja vähennyslaskutoiminnon, joka rajoittui murtolukuihin.

Juuret ja valtuudet

On olemassa yhden desimaalin (C ja D), kahden desimaalin (A ja B) ja kolmen desimaalin (K) asteikkoja. Laskettaessa x 2 {\displaystyle x^{2}} esimerkiksi sijoittamalla x D-asteikolle ja lukemalla sen neliö A-asteikolla. Kääntämällä tämä prosessi toisin päin voidaan löytää neliöjuuret ja samoin potenssit 3, 1/3, 2/3 ja 3/2. Varovaisuutta on noudatettava, kun perusluku x löytyy useammasta kuin yhdestä paikasta asteikollaan. Esimerkiksi asteikolla A on kaksi ysiä; yhdeksän neliöjuuren löytämiseksi käytetään ensimmäistä; toinen antaa 90:n neliöjuuren.

x y {\displaystyle x^{y}} -ongelmissa käytä LL-asteikkoja. Kun LL-asteikkoja on useita, käytä sitä, jossa on x. Kohdista ensin C-asteikon vasemmanpuoleisin 1 LL-asteikon x:n kanssa. Etsi sitten y C-asteikolla ja siirry LL-asteikolle, jossa on x. Tämä asteikko näyttää vastauksen. Jos y on "asteikon ulkopuolella", etsi x y / 2 {\displaystyle x^{y/2}} ja neliöi se käyttämällä A- ja B-asteikkoa edellä kuvatulla tavalla.

Trigonometria

S-, T- ja ST-asteikkoja käytetään trigonometristen funktioiden ja trigonometriatoimintojen kertalukujen, asteina ilmaistujen kulmien, mittaamiseen. Monissa liukusäätimissä on S-, T- ja ST-asteikot merkitty asteilla ja minuuteilla. Ns. decitrig-malleissa käytetään sen sijaan asteiden desimaalimurtolukuja.

Logaritmit ja eksponentit

Perus-10 logaritmit ja eksponentit löytyvät käyttämällä L-asteikkoa, joka on lineaarinen. Joissakin liukusäätimissä on Ln-asteikko, joka on tarkoitettu emäkselle e.

Ln-asteikon keksi 11. luokan oppilas Stephen B. Cohen vuonna 1958. Alkuperäisenä tarkoituksena oli antaa käyttäjälle mahdollisuus valita eksponentti x (välillä 0-2,3) Ln-asteikolla ja lukea e^x C-asteikolla (tai D-asteikolla) ja e^–x CI-asteikolla (tai DI-asteikolla). Pickett, Inc. sai yksinoikeudet asteikkoon. Myöhemmin keksijä loi Ln-asteikolle joukon "merkkejä" laajentaakseen aluetta 2,3:n rajan yli, mutta Pickett ei koskaan sisällyttänyt näitä merkkejä mihinkään liukusäätimiinsä.

Yhteen- ja vähennyslasku

Liukusääntöjä ei yleensä käytetä yhteen- ja vähennyslaskuun, mutta se on kuitenkin mahdollista tehdä kahdella eri tekniikalla.

Ensimmäinen menetelmä yhteen- ja vähennyslaskun suorittamiseksi C- ja D-asteikoilla (tai muilla vastaavilla asteikoilla) edellyttää ongelman muuttamista jako-ongelmaksi. Yhteenlaskussa kahden muuttujan yhteenlaskettu ja yksi kertaa jakaja on yhtä suuri kuin niiden summa:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Kun kyseessä on vähennyslasku, kahden muuttujan suhde, josta on vähennetty yksi kertaa jakaja, on yhtä suuri kuin niiden erotus:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}

Menetelmä on samanlainen kuin yhteen- ja vähennyslaskutekniikka, jota käytetään logaritmisella lukujärjestelmällä varustetuissa nopeissa elektroniikkapiireissä ja erikoistuneissa tietokonesovelluksissa, kuten Gravity Pipe (Gravity Pipe) -supertietokoneessa ja piilotetuissa Markovin malleissa.

Toisessa menetelmässä käytetään liukuvaa lineaarista L-asteikkoa, joka on saatavilla joissakin malleissa. Yhteen- ja vähennyslasku suoritetaan liu'uttamalla kursoria vasemmalle (vähennyslasku) tai oikealle (yhteenlasku) ja palauttamalla liuku 0:een tuloksen lukemiseksi.

 

Fyysinen suunnittelu

Tavalliset lineaariset säännöt

Laskutason pituus ilmoitetaan asteikon nimellispituutena. Yleisimpien "10-tuumaisten" mallien asteikot ovat itse asiassa 25 cm pitkiä, koska ne on valmistettu metristen standardien mukaan, vaikka joissakin säännöissä on hieman pidemmät asteikot, jotka helpottavat manipulointia, kun tulos valuu yli. Taskusäännöt ovat tyypillisesti 5 tuuman mittaisia. Parin metrin pituisia malleja myytiin luokkahuoneisiin ripustettaviksi opetustarkoituksiin. [1]

Tyypillisesti osastot merkitsevät asteikon kahden merkitsevän luvun tarkkuudella, ja käyttäjä arvioi kolmannen luvun. Joissakin huippuluokan laskutikuissa on suurentavat kursorit, joiden avulla merkinnät ovat helpommin nähtävissä. Tällaiset kursorit voivat käytännössä kaksinkertaistaa lukemien tarkkuuden, jolloin 10-tuumainen laskutikku toimii yhtä hyvin kuin 20-tuumainen.

Lisäksi on kehitetty erilaisia muita mukavuuksia. Trigonometriset asteikot on joskus merkitty kahteen kertaan, mustalla ja punaisella, toisiaan täydentävillä kulmilla, niin sanottu Darmstadtin tyyli. Duplex-liuskoissa on usein päällekkäin joitakin asteikkoja selkäpuolella. Asteikot on usein "jaettu" suuremman tarkkuuden saavuttamiseksi.

Erikoistuneita laskutikkuja keksittiin erilaisia tekniikan, liike-elämän ja pankkitoiminnan aloja varten. Näissä oli usein yhteisiä laskutoimituksia, jotka ilmaistiin suoraan erityisasteikoilla, esimerkiksi lainalaskelmia, optimaalisia ostomääriä tai erityisiä teknisiä yhtälöitä. Esimerkiksi Fisher Controls -yritys jakoi räätälöityä laskutikkua, joka oli mukautettu teollisuuden virtauksen säätöventtiilien oikean koon valitsemiseen käytettävien yhtälöiden ratkaisemiseen.

Pyöreät liukusäätimet

Pyöreitä liukusäätimiä on kahta perustyyppiä, joista toisessa on kaksi kursoria (vasemmalla) ja toisessa liikkuva levy ja yksi kursori (oikealla). Kahdella kursorilla varustetuissa versioissa kerto- ja jakolasku suoritetaan säilyttämällä kursoreiden välinen kulma kiinteänä, kun niitä kierretään kiekon ympäri. Yhden kursorin versio toimii enemmän kuin tavallinen laskutikku, kun asteikot kohdistetaan sopivasti.

Pyöreän liukusäätimen perusetu on se, että työkalun pisin ulottuvuus on pienentynyt noin 3-kertaiseksi (eli π:llä). Esimerkiksi 10 cm:n ympyrän uloimman asteikon tarkkuus vastaisi suurimmillaan 30 cm:n tavallisen liukusäätimen tarkkuutta. Pyöreät liukusäätimet estävät myös "mittakaavan ulkopuoliset" laskutoimitukset, koska asteikot on suunniteltu niin, että ne "kiertyvät ympäri"; niitä ei tarvitse koskaan suunnata uudelleen, kun tulokset ovat lähellä 1,0:aa - liukusääntö on aina mittakaavan mukainen. Epäsyklisten, ei-kierteisten asteikkojen, kuten S-, T- ja LL-asteikkojen, asteikon pituus kuitenkin lyhenee, jotta loppumarginaaleille jää tilaa.

Pyöreät liukusäätimet ovat mekaanisesti kestävämpiä ja pehmeämmin liikkuvia, mutta niiden asteikon kohdistustarkkuus on herkkä keskeisen nivelen keskipisteelle; 0,1 mm:n poikkeama nivelen keskipisteestä voi pahimmassa tapauksessa aiheuttaa 0,2 mm:n kohdistusvirheen. Nivel estää kuitenkin asteikon pinnan ja kursorien naarmuuntumisen. Suurimman tarkkuuden asteikot on sijoitettu ulkorenkaisiin. Korkealuokkaisissa pyöreissä asteikoissa käytetään "jaettujen" asteikkojen sijasta kierreasteikkoja monimutkaisempiin operaatioihin, kuten log-of-log-asteikkoihin. Eräässä kahdeksan tuuman premium-sirkkelissä oli 50 tuuman spiraalimainen log-log-asteikko.

Pyöreiden liukusäätimien suurimmat haitat ovat vaikeus paikantaa lukuja pyörivää levyä pitkin ja asteikkojen rajallinen määrä. Toinen pyöreiden liukusäätimien haittapuoli on se, että vähemmän tärkeät asteikot ovat lähempänä keskipistettä, ja niiden tarkkuus on pienempi. Useimmat opiskelijat oppivat käyttämään liukusääntöjä lineaarisilla liukusäätimillä, eikä heillä ollut syytä vaihtaa niitä.

Yksi edelleen päivittäin käytössä oleva laskutikku ympäri maailmaa on E6B. Kyseessä on pyöreä laskutikku, joka kehitettiin ensimmäisen kerran 1930-luvulla lentäjiä varten kuolleen laskennan helpottamiseksi. Kehykseen painettujen asteikkojen avulla se auttaa myös erilaisissa tehtävissä, kuten ajan, etäisyyden, nopeuden ja lämpötilan muuntamisessa, kompassivirheiden selvittämisessä ja polttoaineen kulutuksen laskemisessa. Niin sanottua "rukouspyörää" on edelleen saatavilla lentokonekaupoista, ja sitä käytetään edelleen laajalti. Vaikka GPS on vähentänyt kuolleen reunaehdon käyttöä lentosuunnistuksessa, ja kämmenlaskimet ovat ottaneet haltuunsa monia sen toimintoja, E6B:tä käytetään edelleen laajalti ensisijaisena tai varalaitteena, ja suurin osa lentokouluista vaatii oppilaitaan hallitsemaan sen jossain määrin.

Vuonna 1952 sveitsiläinen kelloyhtiö Breitling esitteli lentäjän rannekellon, jossa oli integroitu pyöreä laskutikku, joka oli erikoistunut lentolaskentaan: Breitling Navitimer. Navitimer-kierroslaskurissa, jota Breitling kutsui "navigointitietokoneeksi", oli lentonopeus-, nousu- ja laskeutumisnopeus-, nousu- ja laskeutumisaika-, lentoaika-, etäisyys- ja polttoaineenkulutustoiminnot sekä kilometrin ja meripeninkulman sekä gallonan ja litran polttoainemäärän muuntotoiminnot.

Materiaalit

Perinteisesti laskutikut valmistettiin kovasta puusta, kuten mahongista tai puksipuusta, ja niiden kursorit olivat lasia tai metallia. Ainakin yksi korkean tarkkuuden väline oli valmistettu teräksestä.

Vuonna 1895 japanilainen yritys Hemmi alkoi valmistaa laskutikkuja bambusta, jonka etuna oli, että se oli mittasuhteiltaan vakaa, vahva ja luonnostaan itsevoiteleva. Nämä bambusta valmistetut liukusäätimet otettiin käyttöön Ruotsissa syyskuussa 1933 [2] ja luultavasti Saksassa hieman aikaisemmin. Asteikot tehtiin selluloidista tai muovista. Myöhemmin laskutikut tehtiin muovista tai muovilla maalatusta alumiinista. Myöhemmin kursorit olivat akryyliä tai polykarbonaattia, jotka liukuvat teflonlaakereilla.

Kaikkiin premium-luokan laskutikkuihin kaiverrettiin numerot ja asteikot, jotka täytettiin maalilla tai muulla hartsilla. Maalattuja tai painettuja laskutikkuja pidettiin huonompina, koska merkinnät saattoivat kulua pois. Pickett, luultavasti Amerikan menestynein laskutikkuyritys, valmisti kuitenkin kaikki painetut asteikot. Korkealuokkaisiin laskutikkuihin kuului ovelat salvat, jotta laskutikku ei hajoaisi vahingossa, ja puskurit, jotka suojasivat asteikkoja ja kursoria hankautumiselta pöytätasoihin. Kaiverrettujen merkintöjen suositeltu puhdistusmenetelmä on hangata kevyesti teräsvillalla. Maalattujen laskutikkujen ja heikkohermoisten kannattaa käyttää laimennettua kaupallista ikkunanpesunestettä ja pehmeää liinaa.

 
Yksinkertainen pyöreä laskutikku, jonka on valmistanut Concise Co., Ltd., Tokio, Japani, ja jossa on vain käänteis-, neliö- ja kuutioasteikot. Kääntöpuolella on kätevä luettelo 38 metrijärjestelmän ja keisarikunnan välisestä muuntokertoimesta.  


Breitling Navitimer rannekello, jossa on pyöreä liukusääntö  


Pickettin pyöreä laskutikku, jossa on kaksi kursoria. (Halkaisija 4,25 tuumaa/10,9 cm) Kääntöpuolella on lisäasteikko ja yksi kursori.  

Historia

Laskutikku keksittiin noin vuosina 1620-1630, pian sen jälkeen kun John Napier oli julkaissut logaritmin käsitteen. Edmund Gunter Oxfordista kehitti laskulaitteen, jossa oli yksi logaritmiskaala ja jota voitiin käyttää lisämittareiden avulla kerto- ja jakolaskuun. Ensimmäisen kuvauksen tästä asteikosta julkaisi Pariisissa vuonna 1624 englantilainen matemaatikko Edmund Wingate (n. 1593 - 1656) kirjassaan "L'usage de la reigle de proportion en l'arithmetique & geometrie". Kirjassa on kaksoisasteikko, jonka toisella puolella on logaritminen asteikko ja toisella puolella taulukkoasteikko. Vuonna 1630 William Oughtred Cambridgesta keksi pyöreän laskutikun, ja vuonna 1632 hän yhdisti kaksi Gunterin laskutikkua, joita pidettiin käsillä yhdessä, ja muodosti laitteen, joka on tunnistettavasti nykyaikainen laskutikku. Kuten aikalaisensa Cambridgessä, Isaac Newton, Oughtred opetti ideoitaan yksityisesti oppilailleen, mutta viivytteli niiden julkaisemisessa, ja Newtonin tavoin hän joutui kiivaaseen kiistaan etuoikeudesta, jossa oli mukana hänen entinen oppilaansa Richard Delamain ja Wingaten aiemmat vaatimukset. Oughtredin ajatukset julkistettiin vasta hänen oppilaansa William Forsterin julkaisuissa vuosina 1632 ja 1653.

Vuonna 1677 Henry Coggeshall loi kahden jalan taittosäännön puutavaran mittausta varten, jota kutsuttiin Coggeshallin liukusäädöksi. Hänen suunnittelunsa ja työkalun käyttötarkoitukset antoivat liukusäätimelle tarkoituksen matemaattisen tutkimuksen ulkopuolella.

Vuonna 1722 Warner otti käyttöön kahden ja kolmen vuosikymmenen asteikot, ja vuonna 1755 Everard otti mukaan käänteisen asteikon; kaikkia näitä asteikkoja sisältävä laskutikku tunnetaan yleensä nimellä "monivaiheinen" laskutikku.

Vuonna 1815 Peter Roget keksi log log liukusäännön, joka sisälsi logaritmin logaritmia esittävän asteikon. Näin käyttäjä pystyi suorittamaan suoraan juuria ja eksponentteja sisältäviä laskutoimituksia. Tämä oli erityisen hyödyllistä murtoluvuille.

Nykyaikainen muoto

Nykyaikaisemman muodon loi vuonna 1859 ranskalainen tykistöluutnantti Amédée Mannheim, "joka oli onnekas, kun hänen sääntönsä valmisti kansallisesti tunnettu yritys ja Ranskan tykistö otti sen käyttöön". Samoihin aikoihin, kun insinöörityöstä tuli tunnustettu ammattitoiminta, liukusääntöjä alettiin käyttää laajalti Euroopassa. Yhdysvalloissa ne yleistyivät vasta vuonna 1881, jolloin Edwin Thacher esitteli siellä lieriömäisen laskutason. Kahdenkertaisen laskutason keksi William Cox vuonna 1891, ja sitä valmisti newyorkilainen Keuffel and Esser Co.

Tähtitieteellinen työ vaati myös hienoja laskutoimituksia, ja 1800-luvun Saksassa eräässä observatoriossa käytettiin noin kahden metrin pituista teräksistä laskutikkua. Siihen oli kiinnitetty mikroskooppi, joka antoi sille kuuden desimaalin tarkkuuden.

Toisessa maailmansodassa pommimiehet ja navigaattorit, jotka tarvitsivat nopeita laskutoimituksia, käyttivät usein erityisiä laskutikkuja. Eräässä Yhdysvaltain laivaston toimistossa suunniteltiin itse asiassa yleinen laskutikkurunkoinen "alusta", jossa oli alumiinirunko ja muovinen kursori, johon voitiin sijoittaa selluloidikortteja (jotka oli painettu molemmille puolille) erikoislaskelmia varten. Menetelmä keksittiin lentokoneiden kantaman, polttoaineen kulutuksen ja korkeuden laskemiseen, ja sitä mukautettiin myöhemmin moniin muihin tarkoituksiin.

Koko 1950- ja 1960-luvun ajan laskutikku oli insinöörin ammatin symboli (samalla tavalla kuin stetoskooppi symboloi lääkärin ammattia). Saksalainen rakettitutkija Wernher von Braun toi mukanaan kaksi 1930-luvun Nestlerin laskutikkuja, kun hän muutti Yhdysvaltoihin toisen maailmansodan jälkeen työskentelemään Yhdysvaltain avaruusohjelman parissa. Hän ei koko elämänsä aikana käyttänyt muita taskulaskimia, vaan laskutikut sopivat hänelle erinomaisesti nopeiden arvioiden tekemiseen rakettien suunnitteluparametreista ja muista luvuista. Alumiinisia Pickett-merkkisiä laskutikkuja kuljetettiin viidellä Apollo-avaruuslennolla, myös kuuhun, Pickettin N600-laskutikkulaatikoiden mainosten mukaan [3].

Jotkut insinööriopiskelijat ja insinöörit kantoivat kymmenen tuuman laskutikkuja vyökoteloissa, ja vielä 1970-luvun puoliväliin asti tämä oli yleinen näky kampuksilla. Opiskelijat saattoivat myös pitää kymmenen tai kahdenkymmenen tuuman laskutikkuja tarkkaa työtä varten kotona tai toimistossa ja kuljettaa mukanaan viiden tuuman taskusääntöä.

Vuonna 2004 kasvatustieteilijät David B. Sher ja Dean C. Nataro kehittivät uudenlaisen laskutason, joka perustui prostaferesiin, logaritmeja edeltävään algoritmiin, jolla voidaan laskea tuotteita nopeasti. Tällaisen laskutason rakentaminen ei kuitenkaan ole herättänyt juurikaan käytännön kiinnostusta alkuperäisen prototyypin jälkeen. [4] Arkistoitu 2005-05-10 Wayback Machine:iin.

Lasku

Laskutikun merkitys alkoi vähentyä, kun elektroniset tietokoneet, jotka olivat 1950-luvulla uusi mutta hyvin niukka resurssi, tulivat laajalti teknisen alan työntekijöiden saataville 1960-luvulla. Fortranin käyttöönotto vuonna 1957 teki tietokoneista käytännöllisiä pienempien matemaattisten ongelmien ratkaisemiseen. IBM toi markkinoille sarjan edullisempia tietokoneita, IBM 650 (1954), IBM 1620 (1959) ja IBM 1130 (1965), jotka oli suunnattu tiede- ja insinöörimarkkinoille. John Kemenyn BASIC-ohjelmointikieli (1964) teki tietokoneiden käytöstä helppoa opiskelijoille. DEC PDP-8 -minitietokone esiteltiin vuonna 1965.

Tietokoneet muuttivat myös laskennan luonnetta. Laskutoimituksissa painotettiin paljon algebran käyttöä, jotta lausekkeet saataisiin mahdollisimman laskettavissa olevaan muotoon. Laskutoimitusten yksinkertaistamiseksi laskutoimitusten käyttäjät yksinkertaisesti likiarvoistivat tai jättivät pois pieniä termejä. Fortranin avulla monimutkaiset kaavat voitiin kirjoittaa oppikirjoista ilman uudelleenmuotoilun vaivaa. Numeerinen integrointi oli usein helpompaa kuin vaikeiden ongelmien ratkaisujen etsiminen suljetussa muodossa. Nuoresta insinööristä, joka pyysi tietokoneaikaa ratkaistakseen ongelman, joka olisi voitu ratkaista muutamalla liukusäätimen pyyhkäisyllä, tuli humoristinen klisee. Monissa tietokonekeskuksissa oli seinälle ripustettu kehystetty laskutikku, jossa luki: "Hätätilanteessa rikkokaa lasi".

Toinen askel kohti laskutikkujen korvaamista elektroniikalla oli tieteelliseen ja tekniseen käyttöön tarkoitettujen elektronisten laskinten kehittäminen. Ensimmäisiä olivat Wang Laboratories LOCI-2, joka esiteltiin vuonna 1965 ja joka käytti logaritmeja kerto- ja jakolaskuissa, sekä Hewlett-Packard HP-9100, joka esiteltiin vuonna 1968. HP-9100:ssa oli eksponenttien ja logaritmien lisäksi trigonometriset funktiot (sin, cos, tan). Se käytti CORDIC-algoritmia (coordinate rotation digital computer), jonka avulla trigonometriset funktiot voidaan laskea käyttämällä vain siirto- ja yhteenlaskuoperaatioita. Tämä menetelmä mahdollisti yhä pienempien tieteellisten laskinten kehittämisen.

Viimeinen naula laskutikun arkkuun oli taskukokoisten tieteellisten laskinten lanseeraus, joista Hewlett-Packardin HP-35 oli ensimmäinen vuonna 1972. Tällaiset laskimet tunnettiin nimellä "laskutikkalaskimet", koska niillä pystyi suorittamaan useimmat tai kaikki laskutikkalaskimen toiminnot. Useiden satojen dollarien hintaisia laskimia pidettiin kalliina useimmille opiskelijoille. Vaikka ammattikäyttöön tarkoitetut laskutikut saattoivat olla myös melko kalliita, apteekit myivät usein muovisia perusmalleja alle 20 dollarilla. Vuoteen 1975 mennessä nelitoimisia elektronisia peruslaskimia sai kuitenkin alle 50 dollarilla. Vuoteen 1976 mennessä TI-30 tarjosi tieteellisen laskimen alle 25 dollarilla. Tämän jälkeen laskutikkujen markkinat ehtyivät nopeasti, kun pienistä tieteellisistä laskimista tuli edullisia.

 
TI-30  


William Oughtred (1575-1660), pyöreän laskutason keksijä.  


Insinööri, joka käyttää laskutikkua. Taustalla mekaaninen laskin.  

Edut

• Liukusäännöllä on taipumus lieventää "väärän tarkkuuden" ja merkityksen harhaa. Tyypillinen tarkkuus, joka on laskutason käyttäjän käytettävissä, on noin kolmen paikan tarkkuus. Tämä vastaa hyvin suurinta osaa teknisiin kaavoihin syötettävistä tiedoista. Nykyaikaista taskulaskinta käytettäessä tarkkuus voidaan ilmoittaa seitsemään tai useampaan desimaaliin asti, vaikka todellisuudessa tulokset eivät voi koskaan olla tarkempia kuin käytettävissä olevat syöttötiedot.
• Liukusääntö edellyttää tulosten suuruusluokan jatkuvaa arviointia. Liukusäätimellä 1,5 × 30 (joka on 45) näyttää saman tuloksen kuin 1 500 000 × 0,03 (joka on 45 000). Insinöörin tehtävänä on jatkuvasti määritellä tulosten kohtuullisuus, mikä voidaan menettää, kun luvut syötetään huolimattomasti tietokoneohjelmaan tai laskimeen.
• Kun suoritetaan sarja kerto- tai jakolaskuja samalla luvulla, vastaus voidaan usein määrittää pelkällä silmäyksellä laskutikkuun ilman minkäänlaista manipulointia. Tämä voi olla erityisen hyödyllistä, kun lasketaan prosenttilukuja, esimerkiksi testituloksia, tai kun vertaillaan hintoja, esimerkiksi dollareita kiloa kohti. Useita nopeus-aika-etäisyyslaskelmia voidaan suorittaa kädet vapaina yhdellä silmäyksellä laskutikulla.
• Laskutikku ei ole riippuvainen sähköstä.
• Laskutikku on helposti jäljiteltävissä oleva tekniikka. Pätevä käsityöläinen voi rakentaa enemmänkin laskutikkuja alkeellisista materiaaleista käyttäen ei-teollisia prosesseja.
• Liukusäännöt ovat pitkälle standardoituja, joten mitään ei tarvitse opetella uudelleen, kun siirrytään toiseen sääntöön.
• Liukusäätimet ovat monipuolisia, ja niitä voidaan käyttää tilanteissa ja ympäristöissä, joissa ihmiskäyttäjän sorminäppäryys saattaa olla heikentynyt (esimerkiksi suojakäsineiden käytön vuoksi). Sitä vastoin laskinta voi olla vaikea käyttää tällaisissa tilanteissa - laskutikun käyttö ei todennäköisesti aiheuta samanlaista virhettä kuin laskimen väärän painikkeen painaminen vahingossa.
• Liukusääntöjä voidaan tehdä pahvista tai paperista. Monet kartongista valmistetut ilmaiset taulukot tai erikoislaskentalaitteet ovat itse asiassa erikoistuneita lineaarisia tai pyöreitä laskutikkuja.

Yksi etu, joka saadaan käyttämällä laskutikkua yhdessä elektronisen laskimen kanssa, on se, että tärkeät laskutoimitukset voidaan tarkistaa tekemällä ne molemmilla välineillä; koska nämä kaksi välinettä ovat niin erilaisia, on pieni mahdollisuus tehdä sama virhe kahdesti.

 

Haitat

• Virheet voivat johtua mekaanisesta epätarkkuudesta.
• Laskutoimitusten tarkkuus on rajoitettu laskutoimitusten analogisten tulojen ja lähtöjen vuoksi. Sitä vastoin diskreetin numeerisen syötteen ja liukulukujen elektronisten operaatioiden ansiosta vaatimattomienkin nykyaikaisten laskinten ulostulon tarkkuus on vähintään kuusi merkitsevää numeroa.

 

Aiheeseen liittyvät sivut

• Abacus
• Logaritmi