Bändiaukko (energia-aukko): määritelmä ja merkitys puolijohteissa

Bändiaukko (energia-aukko) selitetty: mitä se on, miten se vaikuttaa puolijohteiden sähkönjohtavuuteen ja miksi se on keskeinen elektroniikassa.

Tekijä: Leandro Alegsa

12-02-2026 23:07

Bändiaukko, jota kutsutaan myös nimellä bandgap tai energia-aukko, on kiinteässä aineessa oleva energia-alue, jossa ei voi olla elektronitiloja. Termi on keskeinen sekä kiinteän aineen fysiikassa että kemiassa. Bändiaukon suuruus määrää, kuinka helposti elektroneja voidaan siirtää valenssikaistan yläosasta johtokaistaan, ja siten se vaikuttaa aineen sähköisiin ja optisiin ominaisuuksiin.

Mitä bändiaukko tarkoittaa käytännössä?

Elektronit voivat kiinteässä aineessa täyttää tietyt energiatilat. Valenssikaistan elektronit ovat sidoksissa atomeihin, kun taas johtokaistassa olevat elektronit voivat liikkua vapaasti ja kuljettaa varauksia. Bändiaukko on näiden kaistojen välinen energiaero: energia, joka tarvitaan vapauttamaan elektronin ulkokuorelta niin, että siitä tulee liikkuva varauksenkuljettaja. Toisin sanoen ainoastaan, kun elektroni saa vähintään bändiaukon verran energiaa, se voi siirtyä johtokaistaan ja lisätä materiaalin johtavuutta.

Yksiköt ja tyypilliset arvot

Bändiaukon suuruus ilmoitetaan yleisesti elektronivoltteina). Esimerkkejä tyypillisistä bändiaukoista:

Piillä (Si) noin 1,12 elektronivoltteina)
Germaniumilla (Ge) noin 0,66 elektronivoltteina)
GaAs:lla noin 1,42 elektronivoltteina)

Suuret bändiaukot tekevät materiaalista yleensä hyvän eristeen, pienemmät bändiaukot luonnehtivat puolijohteita, ja Johtajilla bändit voivat olla päällekkäisiä tai aukko erittäin pieni, jolloin johtokyky on korkea.

Suorat ja epäsuorat bändiaukot

Puolijohteiden bändiaukot ovat joko suoria tai epäsuoria. Suorassa bändiaukossa johtokaistan alin ja valenssikaistan ylin kohta sijaitsevat samalla aaltoluvulla, joten elektroni voi siirtyä kaistojen välillä absorboimalla tai emittoimalla photonin ilman että fononi (verkkoäännen kvantti) osallistuu. Tämä tekee materiaaleista, kuten GaAs, tehokkaita valonlähteinä (LEDit, laserit). Epäsuorassa bändiaukossa, kuten piillä, siirtymiseen tarvitaan myös fononi, mikä tekee optisista prosesseista vähemmän tehokkaita.

Vaikutus sähkönjohtavuuteen ja lämpötilariippuvuus

Bändiaukon suuruus määrää intrinsisen (puhtaan) puolijohteen kantajien tiheyden. Lämpöenergia voi eksitoida elektroneja valenssista johtoon: mitä pienempi bändiaukko, sitä helpommin lämpö voi tuottaa johtavia elektroneja. Tämän vuoksi puolijohteiden johtavuus kasvaa lämpötilan noustessa. Lisäksi bändiaukko yleensä pienenee hieman lämpötilan noustessa johtuen kiderakenteen laajenemisesta ja elektronien vuorovaikutuksista.

Doping ja ekstruusiivinen johtavuus

Puolijohteiden johtavuutta voidaan säädellä tarkoituksellisesti dopingilla eli lisäämällä pieniä määriä epäpuhtauksia, jotka luovuttavat elektroneja (donorit) tai vastaanottavat elektroneja (akseptorit). Doping muuttaa Fermin tason sijaintia ja kasvattaa vapaita kantajia ilman, että tarvitaan suurta lämpöenergian syöttöä bändiaukon ylittämiseksi. Tällä periaatteella toimivat mm. transistori- ja diodipiirit.

Optiset ominaisuudet ja sovellukset

Bändiaukon energia määrittää myös materiaalin absorptio- ja emittoivan valon aallonpituuden: fotonin energia pitää olla vähintään bändiaukon suuruinen, jotta se absorboituu ja synnyttää elektronin ja aukon parin. Tämä on keskeistä esimerkiksi aurinkokennoissa, valoemissiivisissa diodeissa ja fotodetektoreissa. Puolijohdemateriaalien valinta säädetään halutun toiminnan ja aallonpituuden mukaan.

Mittaaminen ja teoreettinen kuvaus

Bändiaukkoa mitataan spektroskopian, optisen absorbtion ja fotoelektronisen spektroskopian menetelmin sekä lasketaan teoreettisesti kvasihiukkas- ja tiheysfunktionaaliteorian (DFT) kaltaisilla menetelmillä. Käytännössä mitattu arvo voi riippua esimerkiksi dopauksesta, pinnan olomuodosta ja lämpötilasta.

Yhteenvetona: bändiaukko on peruskäsite, joka selittää, miksi aineet käyttäytyvät eristeinä, puolijohteina tai johtimina, ja se määrittää olennaisesti materiaalien sähköiset ja optiset ominaisuudet sekä niiden soveltuvuuden elektroniikkaan ja fotoniikkaan. Bändiaukon hallinta — materiaalivalinnalla, valmistusmenetelmillä ja dopauksella — on puolijohdeteknologian perusta.

Puolijohdefysiikassa

Tutkijat käyttävät kaistaväliä ennustamaan, johtaako kiinteä aine sähköä. Useimmat elektronit (valenssielektronit) vetävät puoleensa vain yhden atomin ydintä. Mutta jos elektronilla on tarpeeksi energiaa lentääkseen pois lähimmästä ytimestä, se voi osallistua sähkövirran kulkuun kiinteän aineen muodostavien monien atomien välillä. Elektroneita, jotka eivät ole tiukasti kiinni vain yhdessä ytimessä, kutsutaan johtokaistaksi.

Puolijohteissa ja eristeissä kvanttimekaniikka osoittaa, että elektroneja on vain tietyissä energiakaistoissa. Muilta energiatasoilta elektronit on kielletty. Termi kaistaväli viittaa energiaeroon valenssikaistan yläosan ja johtokaistan alaosan välillä. Elektronit pystyvät hyppäämään kaistasta toiseen. Elektroni tarvitsee kuitenkin tietyn energiamäärän hypätäkseen valenssikaistasta johtokaistalle. Tarvittava energiamäärä vaihtelee eri materiaaleissa. Elektronit voivat saada tarpeeksi energiaa hyppyäkseen johtokaistalle absorboimalla joko fononin (lämpöä) tai fotonin (valoa).

Puolijohde on materiaali, jolla on pieni, mutta nollasta poikkeava kaistaväli ja joka käyttäytyy eristävänä aineena absoluuttisessa nollalämpötilassa (0 K), mutta sallii lämmön herättää elektroneja riittävästi hyppäämään johtavuuskaistalleen lämpötiloissa, jotka ovat alle sen sulamispisteen. Sitä vastoin materiaali, jolla on suuri kaistaväli, on eriste. Johtimissa valenssi- ja johtumiskaistat voivat olla päällekkäisiä, joten niillä ei välttämättä ole kaistaleveyttä.

Sisäisten puolijohteiden johtavuus riippuu vahvasti kaistanvälistä. Ainoat johtavuuteen käytettävissä olevat kantajat ovat elektronit, joilla on riittävästi lämpöenergiaa innostuakseen kaistanraon yli.

Kaistaväli-tekniikka on prosessi, jossa materiaalin kaistaväliä hallitaan tai muutetaan tiettyjen puolijohdeseosten, kuten GaAlAs:n, InGaAs:n ja InAlAs:n, koostumusta säätelemällä. On myös mahdollista rakentaa kerrosmateriaaleja, joiden koostumus vaihtelee, esimerkiksi molekyylisäteen epitaksia-tekniikalla. Näitä menetelmiä käytetään heterojunktion bipolaaritransistorien (HBT), laserdiodien ja aurinkokennojen suunnittelussa.

Puolijohteiden ja eristeiden välille on vaikea vetää rajaa. Yksi tapa on ajatella puolijohteita eräänlaisina eristeinä, joilla on kapea kaistaväli. Eristeitä, joilla on suurempi, yleensä yli 3 eV:n kaistanväli, ei luokitella puolijohderyhmään, eivätkä ne yleensä käyttäydy puolijohteisesti käytännön olosuhteissa. Elektronien liikkuvuudella on myös merkitystä määritettäessä materiaalin epävirallista ryhmittelyä puolijohteeksi.

Puolijohteiden kaistanhalkaisijan energia pyrkii pienenemään lämpötilan noustessa. Lämpötilan noustessa atomivärähtelyjen amplitudi kasvaa, mikä johtaa suurempaan atomien väliseen etäisyyteen. Myös ristikkofononien ja vapaiden elektronien ja aukkojen välinen vuorovaikutus vaikuttaa hieman kaistanväliin. Bändiaukkoenergian ja lämpötilan välistä suhdetta voidaan kuvata Varshnin empiirisellä lausekkeella,

E g ( T ) = E g ( 0 ) - α T 2 T + β {\displaystyle E_{g}(T)=E_{g}(0)-{\frac {\alpha T^{2}}{T+\beta }}} $E_{g}(T)=E_{g}(0)-{\frac {\alpha T^{2}}{T+\beta }}$ , missä E_g (0), α ja β ovat aineellisia vakioita.

Tavallisessa puolijohdekiteessä kaistaväli on kiinteä jatkuvien energiatilojen vuoksi. Kvanttipistekiteessä kaistaväli riippuu koosta, ja sitä voidaan muuttaa siten, että valenssikaistan ja johtavuuskaistan välille saadaan erilaisia energioita. Se tunnetaan myös nimellä kvanttirajausvaikutus.

Kaistahalkeamat riippuvat myös paineesta. Kaistahalkeamat voivat olla joko suoria tai epäsuoria, riippuen elektronisesta kaistarakenteesta.

Matemaattinen tulkinta

Klassisesti todennäköisyyksien suhde sille, että elektroni miehittää kaksi tilaa, joiden energiaero ΔE on, on Boltzmannin kerroin:

e ( - Δ E k T ) {\displaystyle e^{\left({\frac {-\Delta E}{kT}}\right)}} $e^{\left({\frac {-\Delta E}{kT}}\right)}$

missä:

e on Eulerin luku (luonnollisten logaritmien perusta). e on Eulerin luku.
ΔE on energiaero
k on Boltzmannin vakio
T on lämpötila.

Fermi-tasolla (tai kemiallisessa potentiaalissa) tilan miehityksen todennäköisyys on ½. Jos Fermi-taso on keskellä 1 eV:n kaistanväliä, tämä todennäköisyys on e⁻²⁰ eli noin 2,0⋅10⁻⁹ huoneenlämpötilan lämpöenergian ollessa 25,9 meV.

Aurinkokennot

Valo ja lämpö voivat herättää elektroneja. Kaistaväli määrittää, minkä osan auringon spektristä aurinkokenno absorboi. Luminesenssiaurinkomuuntimessa käytetään luminesenssimediaa muuntamaan fotonit, joiden energia on kaistanraon yläpuolella, fotonienergioiksi, jotka ovat lähempänä aurinkokennon sisältävän puolijohteen kaistanrajaa.

Luettelo kaistaväleistä

Materiaali	Symboli	Bändiaukko (eV) @ 302K	Viite
Pii	Si	1.11
Seleeni	Se	1.74
Germanium	Ge	0.67
Piikarbidi	SiC	2.86
Alumiinifosfidi	AlP	2.45
Alumiiniarsenidi	AlAs	2.16
Alumiiniantimonidi	AlSb	1.6
Alumiininitridi	AlN	6.3
Timantti	C	5.5
Gallium(III)fosfidi	GaP	2.26
Gallium(III)arsenidi	GaAs	1.43
Gallium(III)nitridi	GaN	3.4
Gallium(II)sulfidi	GaS	2.5
Galliumantimonidi	GaSb	0.7
Indiumantimonidi	InSb	0.17
Indium(III)nitridi	InN	0.7
Indium(III)fosfidi	InP	1.35
Indium(III)arsenidi	InAs	0.36
Raudan disilisidit	β-FeSi₂	0.87
Sinkkioksidi	ZnO	3.37
Sinkkisulfidi	ZnS	3.6
Sinkkiselenidi	ZnSe	2.7
Sinkkitelluridi	ZnTe	2.25
Kadmiumsulfidi	CdS	2.42
Kadmiumselenidi	CdSe	1.73
Kadmiumtelluridi	CdTe	1.49
Lyijy(II)sulfidi	PbS	0.37
Lyijy(II)selenidi	PbSe	0.27
Lyijy(II)telluridi	PbTe	0.29
Kupari(II)oksidi	CuO	1.2
Kupari(I)oksidi	Cu O₂	2.1

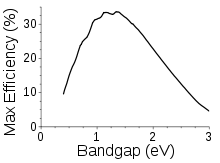
Shockley-Queisserin raja-arvo antaa yhden liitoksen aurinkokennon suurimman mahdollisen hyötysuhteen keskittymättömässä auringonvalossa puolijohteen kaistaleveyden funktiona. Jos kaistanraja on liian korkea, suurinta osaa päivänvalon fotoneista ei voida absorboida; jos se on liian matala, useimmissa fotoneissa on paljon enemmän energiaa kuin tarvitaan elektronien herättämiseen kaistanrajan yli, ja loput menee hukkaan. Kaupallisissa aurinkokennoissa yleisesti käytettyjen puolijohteiden kaistalukot ovat lähellä tämän käyrän huippua, esimerkiksi piin (1,1 eV) tai CdTe:n (1,5 eV). Shockley-Queisserin raja voidaan ylittää tandem-aurinkokennoilla, keskittämällä auringonvaloa kennoon ja muilla menetelmillä.

Puolijohteiden kaistarakenne.

Fotoniikassa ja fononiikassa

Fotoniikassa kaistavälit tai pysäytyskaistat ovat fotonitaajuuksien alueita, joilla fotonit eivät pääse kulkemaan materiaalin läpi, jos tunnelivaikutukset jätetään huomiotta. Materiaalia, jolla on tällainen käyttäytyminen, kutsutaan fotonikiteeksi.

Samanlainen fysiikka pätee myös fononeihin fononisessa kiteessä.

Kysymyksiä ja vastauksia

K: Mikä on kaistaväli?

A: Bändiaukko, jota kutsutaan myös nimellä bandgap tai energia-aukko, on kiinteässä aineessa oleva energia-alue, jossa ei voi olla elektronitiloja.

K: Mitä termi tarkoittaa kiinteän aineen fysiikassa ja kemiassa?

V: Termi viittaa energiaeroon (elektronivoltteina) valenssikaistan yläosan ja johtokaistan alaosan välillä. Tämä tunnetaan myös energiana, joka tarvitaan ulomman kuoren elektronin vapauttamiseen ytimen ympärillä olevalta radaltaan liikkuvaksi varauksenkuljettajaksi.

K: Miten se vaikuttaa sähkönjohtavuuteen?

V: Bändiaukko on tärkeä tekijä, joka määrittää kiinteän aineen sähkönjohtavuuden. Aineet, joilla on suuret kaistahalkeamat, ovat yleensä eristeitä, ja aineet, joilla on pienet kaistahalkeamat, ovat puolijohteita. Johtajilla on joko hyvin pienet kaistahalkeamat tai niitä ei ole lainkaan, jos valenssi- ja johtavuuskaistojen energiatasot ovat päällekkäin.

Kysymys: Miten elektronit liikkuvat kiinteissä aineissa?

V: Elektronit voivat liikkua vapaasti kiinteissä aineissa, kun niistä tulee liikkuvia varauksenkuljettajia sen jälkeen, kun ne ovat vapautuneet ytimiä ympäröiviltä radoiltaan.

K: Mitä tapahtuu, kun elektronit saavuttavat korkeampia energioita?

V: Kun elektronit saavuttavat korkeampia energioita, ne voivat hypätä kaistanraon muodostaman energiaesteen yli ja muuttua vapaiksi elektroneiksi, jotka voivat liikkua vapaasti kiinteässä aineessa.

K: Ovatko kaikki kiinteät aineet eristeitä vai puolijohteita?

V: Kaikki kiinteät aineet eivät ole eristeitä tai puolijohteita; jotkin aineet voivat olla johtimia, jos niiden valenssi- ja johtumiskaistat menevät päällekkäin, jolloin kaistaleväli on hyvin pieni tai sitä ei ole lainkaan.

Etsiä