Kvanttimekaniikka | selittää maailmankaikkeuden toimintaa atomia pienemmässä mittakaavassa

Kvanttimekaniikka selittää, miten maailmankaikkeus toimii atomia pienemmässä mittakaavassa. Sitä kutsutaan myös kvanttifysiikaksi tai kvanttiteoriaksi. Mekaniikka on fysiikan osa, joka selittää, miten asiat liikkuvat, ja kvantti on latinankielinen sana, joka tarkoittaa "kuinka paljon". Energiakvantti on pienin mahdollinen määrä (tai pienin ylimääräinen määrä), ja kvanttimekaniikka kuvaa, miten tämä energia liikkuu tai vuorovaikuttaa.

Atomeja pidettiin pitkään aineen pienimpinä kappaleina, mutta nykyaikainen tiede on osoittanut, että on olemassa vielä pienempiä subatomisia hiukkasia, kuten protoneja, neutroneja ja elektroneja. Kvanttimekaniikka kuvaa, miten atomien muodostavat hiukkaset toimivat.

Kvanttimekaniikka kertoo myös, miten sähkömagneettiset aallot (kuten valo) toimivat. Aalto-hiukkasdualismi tarkoittaa, että hiukkaset käyttäytyvät kuin aallot ja aallot käyttäytyvät kuin hiukkaset. (Ne eivät ole kahdenlaisia asioita, vaan jotain molempien kaltaista: tämä on niiden kaksinaisuus). Suuri osa nykyaikaisesta fysiikasta ja kemiasta voidaan kuvata ja ymmärtää kvanttimekaniikan matemaattisten sääntöjen avulla.

Matematiikka, jota käytetään subatomisten hiukkasten ja sähkömagneettisten aaltojen tutkimiseen, on hyvin monimutkaista, koska ne toimivat hyvin oudoilla tavoilla.




 

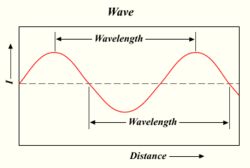
Valoaallon aallonpituus  Zoom
Valoaallon aallonpituus  

Aallot ja fotonit

Fotonit ovat hiukkasia, jotka ovat pistemäisiä, pienempiä kuin atomit. Fotonit ovat ikään kuin "paketteja" tai energiapaketteja. Valonlähteet, kuten kynttilät tai laserit, tuottavat valoa fotoneiksi kutsuttuina palasina.

Mitä enemmän fotoneja lamppu tuottaa, sitä kirkkaampi valo on. Valo on energiamuoto, joka käyttäytyy kuten veden aallot tai radioaallot. Yhden aallon huipun ja seuraavan aallon huipun välistä etäisyyttä kutsutaan aallonpituudeksi. Jokaisessa fotonissa on tietty energiamäärä eli "kvantti", joka riippuu sen aallonpituudesta.

Valon väri riippuu sen aallonpituudesta. Violetin värin (sateenkaaren alin tai sisin väri) aallonpituus on noin 400 nm ("nanometriä"), mikä vastaa 0,00004 senttimetriä tai 0,000016 tuumaa. Fotoneja, joiden aallonpituus on 10-400 nm, kutsutaan ultravioletti- eli UV-valoksi. Ihmissilmä ei voi nähdä tällaista valoa. Spektrin toisessa päässä on punainen valo, jonka aallonpituus on noin 700 nm. Infrapunavalo on noin 700 nm-300 000 nm. Ihmissilmät eivät myöskään ole herkkiä infrapunavalolle.

Aallonpituudet eivät aina ole niin pieniä. Radioaalloilla on pidemmät aallonpituudet. FM-radion aallonpituus voi olla useita metrejä (esimerkiksi 99,5 FM-asemat lähettävät radioenergiaa, jonka aallonpituus on noin 3 metriä eli noin 10 jalkaa). Jokaisella fotonilla on tietty määrä energiaa, joka liittyy sen aallonpituuteen. Mitä lyhyempi fotonin aallonpituus on, sitä suurempi on sen energia. Esimerkiksi ultraviolettifotonilla on enemmän energiaa kuin infrapunafotonilla.

Aallonpituus ja taajuus (kuinka monta kertaa aalto nousee sekunnissa) ovat kääntäen verrannollisia, mikä tarkoittaa, että pidempi aallonpituus on pienempi taajuus ja päinvastoin. Jos valon väri on infrapuna (matalampi taajuus kuin punaisella valolla), jokainen fotoni voi lämmittää sitä, mihin se osuu. Jos siis voimakas infrapunalamppu (lämpölamppu) suunnataan henkilöä kohti, tämä tuntee olonsa lämpimäksi tai jopa kuumaksi, koska moniin fotoneihin on varastoitunut energiaa. Infrapunalampun pinta voi jopa kuumentua niin kuumaksi, että se voi polttaa siihen kosketuksissa olevan henkilön. Ihminen ei näe infrapunavaloa, mutta voi tuntea säteilyn lämmön muodossa. Esimerkiksi auringon lämmittämän tiilirakennuksen ohi kulkeva henkilö tuntee rakennuksen lämmön ilman, että hänen tarvitsee koskea siihen.

Kvanttimekaniikan matemaattiset yhtälöt ovat abstrakteja, mikä tarkoittaa, että hiukkasen tarkkoja fysikaalisia ominaisuuksia (kuten sen sijaintia tai liikemäärää) on mahdotonta tietää varmasti. Sen sijaan matemaattinen funktio, jota kutsutaan aaltofunktioksi, antaa tietoa siitä, millä todennäköisyydellä hiukkasella on tietty ominaisuus. Aaltofunktio voi esimerkiksi kertoa, millä todennäköisyydellä hiukkanen löytyy tietystä paikasta, mutta se ei voi kertoa, missä se on varmasti. Tämän epävarmuuden ja muiden tekijöiden vuoksi et voi käyttää klassista mekaniikkaa (fysiikkaa, joka kuvaa, miten suuret kappaleet liikkuvat) ennustamaan kvanttihiukkasten liikettä.

Ultraviolettivalon taajuus on korkeampi kuin violetin valon, joten se ei kuulu edes näkyvään valoon. Jokaisessa ultraviolettivalon fotonissa on paljon energiaa, joka riittää vahingoittamaan ihosoluja ja aiheuttamaan auringonpolttaman. Itse asiassa useimmat auringonpolttamat eivät johdu lämmöstä, vaan ne johtuvat siitä, että auringon UV-säteiden korkea energia vahingoittaa ihosoluja. Vielä korkeammat valotaajuudet (tai sähkömagneettinen säteily) voivat tunkeutua syvemmälle kehoon ja aiheuttaa vielä enemmän vahinkoa. Röntgensäteissä on niin paljon energiaa, että ne voivat tunkeutua syvälle ihmiskehoon ja tappaa soluja. Ihminen ei voi nähdä tai tuntea ultraviolettivaloa tai röntgensäteitä. Hän voi tietää olleensa tällaisen korkeataajuisen valon vaikutuksen alaisena vasta, kun hän saa säteilypalovamman. Alueilla, joilla on tärkeää tappaa pöpöjä, käytetään usein ultraviolettilamppuja bakteerien, sienten jne. tuhoamiseen. Röntgensäteitä käytetään joskus syöpäsolujen tappamiseen.

Kvanttimekaniikka sai alkunsa, kun havaittiin, että jos hiukkasella on tietty taajuus, sillä on oltava myös tietty määrä energiaa. Energia on verrannollinen taajuuteen (E ∝ f). Mitä suurempi taajuus, sitä enemmän energiaa fotonilla on ja sitä enemmän vahinkoa se voi aiheuttaa. Kvanttimekaniikka kasvoi myöhemmin selittämään atomien sisäistä rakennetta. Kvanttimekaniikka selittää myös tavan, jolla fotoni voi interferoida itsensä kanssa, ja monia muita asioita, joita klassisessa fysiikassa ei osattu kuvitella.

 

Vasemmalla oleva musta on ultraviolettisäteilyä (korkea taajuus), oikealla oleva musta on infrapunasäteilyä (matala taajuus).  Zoom
Vasemmalla oleva musta on ultraviolettisäteilyä (korkea taajuus), oikealla oleva musta on infrapunasäteilyä (matala taajuus).  

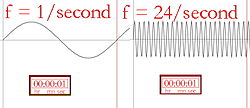
Taajuuden kuvallinen kuvaus  Zoom
Taajuuden kuvallinen kuvaus  

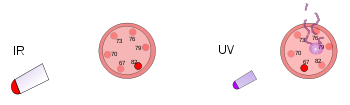
Vasemmalla muovinen lämpömittari on kirkkaan lämpölampun alla. Infrapunasäteily lämmittää mutta ei vahingoita lämpömittaria. Oikealla toinen muovinen lämpömittari joutuu matalan intensiteetin ultraviolettivalon kohteeksi. Tämä säteily vahingoittaa mutta ei lämmitä lämpömittaria.  Zoom
Vasemmalla muovinen lämpömittari on kirkkaan lämpölampun alla. Infrapunasäteily lämmittää mutta ei vahingoita lämpömittaria. Oikealla toinen muovinen lämpömittari joutuu matalan intensiteetin ultraviolettivalon kohteeksi. Tämä säteily vahingoittaa mutta ei lämmitä lämpömittaria.  

Kvantisointi

Max Planck löysi taajuuden ja energian välisen suhteen. Kukaan ei ollut aiemmin arvannut, että taajuus on suoraan verrannollinen energiaan (tämä tarkoittaa, että kun toinen niistä kaksinkertaistuu, myös toinen kaksinkertaistuu). Niin sanotuissa luonnollisissa yksiköissä fotonin taajuutta kuvaava luku edustaisi myös sen energiaa. Yhtälö olisi silloin seuraava:

{\displaystyle E=f}

eli energia on yhtä suuri kuin taajuus.

Mutta fysiikan kehittymisen myötä energian mittaamiseen käytettyjen yksiköiden ja ajan (ja siten taajuuden) mittaamiseen yleisesti käytettyjen yksiköiden välillä ei ollut luonnollista yhteyttä. Niinpä Planck kehitti kaavan, jolla hän sai kaikki luvut täsmäämään:

{\displaystyle E=h\times f}

tai energia on yhtä suuri kuin h kertaa taajuus. Tämä h on luku, jota kutsutaan Planckin vakioksi sen löytäjän mukaan.

Kvanttimekaniikka perustuu tietoon siitä, että tietyn taajuuden fotoni tarkoittaa tietyn energiamäärän fotonia. Tämän suhteen lisäksi tietynlainen atomi voi lähettää vain tietynlaista säteilyä, joten se voi myös lähettää vain tietyn energiamäärän fotoneja.

 

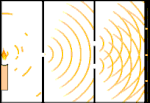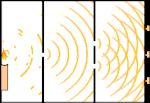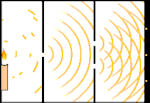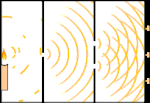
Kaksoissaljakoe: valo kulkee vasemmalla olevasta valonlähteestä oikealla oleviin hapsuihin (merkitty mustalla reunalla).  Zoom
Kaksoissaljakoe: valo kulkee vasemmalla olevasta valonlähteestä oikealla oleviin hapsuihin (merkitty mustalla reunalla).  

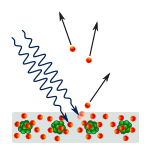
Valosähköinen vaikutus: fotonit osuvat metalliin ja elektronit työntyvät pois.  Zoom
Valosähköinen vaikutus: fotonit osuvat metalliin ja elektronit työntyvät pois.  

Historia

Isaac Newton ajatteli, että valo koostuu hyvin pienistä asioista, joita nykyään kutsumme hiukkasiksi (hän kutsui niitä "korpuskeleiksi"). Christiaan Huygens ajatteli, että valo koostuu aalloista. Tutkijat ajattelivat, että jokin asia ei voi olla samanaikaisesti hiukkanen ja aalto.

Tutkijat tekivät kokeita selvittääkseen, koostuuko valo hiukkasista vai aalloista. He saivat selville, että molemmat ajatukset olivat oikeita - valo oli jotenkin sekä aaltoja että hiukkasia. Thomas Youngin suorittama kaksoisrakokoe osoitti, että valon on toimittava aallon tavoin. Albert Einsteinin havaitsema valosähköinen ilmiö osoitti, että valon oli toimittava hiukkasina, jotka kuljettavat tiettyjä energiamääriä, ja että energiat olivat yhteydessä niiden taajuuksiin. Tätä kokeellista tulosta kutsutaan kvanttimekaniikassa "aalto-hiukkasdualiteetiksi". Myöhemmin fyysikot havaitsivat, että kaikki käyttäytyy sekä aalto- että hiukkasmaisesti, ei vain valo. Tämä vaikutus on kuitenkin paljon pienempi suurissa kohteissa.

Seuraavassa on lueteltu joitakin kvanttimekaniikan perusosat keksineitä henkilöitä: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann ja Richard Feynman. He tekivät työtään 1900-luvun alkupuoliskolla.

 

Vasemmalta oikealle: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.  Zoom
Vasemmalta oikealle: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.  

Planckin ulkopuolella

Kvanttimekaniikan kaavat ja ideat tehtiin selittämään valoa, joka tulee hehkuvasta vedystä. Atomin kvanttiteorian piti myös selittää, miksi elektroni pysyy radallaan, mitä muut ideat eivät pystyneet selittämään. Vanhoista ideoista seurasi, että elektronin olisi pudottava atomin keskipisteeseen, koska se aluksi pysyy radallaan oman energiansa avulla, mutta se menettää nopeasti energiansa kiertäessään radallaan. (Tämä johtuu siitä, että elektronien ja muiden varattujen hiukkasten tiedettiin säteilevän valoa ja menettävän energiaa muuttaessaan nopeuttaan tai kääntyessään).

Vetylamput toimivat kuten neonlamput, mutta neonlampuilla on oma ainutlaatuinen ryhmänsä valon värejä (ja taajuuksia). Tutkijat oppivat, että he voivat tunnistaa kaikki alkuaineet niiden tuottaman valon värin perusteella. He eivät vain saaneet selville, miten taajuudet määräytyivät.

Sitten sveitsiläinen matemaatikko nimeltä Johann Balmer keksi yhtälön, joka kertoi, mikä λ (lambda, aallonpituus) olisi:

\lambda =B\left({\frac {n^{2}}{n^{2}-4}}\right)\qquad \qquad n=3,4,5,6

jossa B on luku, jonka Balmer määritteli olevan 364,56 nm.

Tämä yhtälö toimi vain vetylamppujen näkyvän valon osalta. Myöhemmin yhtälöstä tehtiin kuitenkin yleisempi:

{\frac {1}{\lambda }}=R\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right),

jossa R on Rydbergin vakio, joka on 0,0110 nm−1 , ja n:n on oltava suurempi kuin m.

Kun m:n ja n:n arvot vaihdetaan, on helppo ennustaa monien valotyyppien (ultravioletti, näkyvä valo ja infrapuna) taajuudet. Jos haluat nähdä, miten tämä toimii, mene Hyperphysics-sivustolle ja siirry alas sivun keskikohdan ohi. (Käytä H = 1 vetyä varten.)

Vuonna 1908 Walter Ritz kehitti Ritzin yhdistelmäperiaatteen, joka osoittaa, miten tietyt taajuuksien väliset aukot toistuvat jatkuvasti. Tämä osoittautui tärkeäksi Werner Heisenbergille useita vuosia myöhemmin.

Vuonna 1905 Albert Einstein osoitti Planckin idean avulla, että valonsäde koostuu fotoneiksi kutsutuista hiukkasista. Kunkin fotonin energia riippuu sen taajuudesta. Einsteinin ajatus on alku sille kvanttimekaniikan ajatukselle, että kaikki subatomiset hiukkaset, kuten elektronit, protonit, neutronit ja muut, ovat samanaikaisesti sekä aaltoja että hiukkasia. (Katso kuva atomista, jossa elektroni on aaltona atomissa.) Tämä johti subatomisia hiukkasia ja sähkömagneettisia aaltoja koskevaan teoriaan, jota kutsutaan aalto-hiukkasdualiteetiksi. Siinä hiukkaset ja aallot eivät olleet kumpaakaan, vaan niillä oli tiettyjä ominaisuuksia molemmista.

Vuonna 1913 Niels Bohr keksi, että elektronit voivat kiertää atomin ytimen ympärillä vain tiettyjä ratoja. Bohrin teorian mukaan yllä olevassa yhtälössä esiintyvät luvut m ja n voisivat edustaa kiertoratoja. Bohrin teorian mukaan elektronit voivat aloittaa jollakin radalla m ja päätyä jollakin radalla n tai elektroni voi aloittaa jollakin radalla n ja päätyä jollakin radalla m. Jos siis fotoni osuu elektroniin, sen energia absorboituu, ja elektroni siirtyy korkeammalle radalle ylimääräisen energian ansiosta. Bohrin teorian mukaan, jos elektroni putoaa korkeammalta radalta alemmalle radalle, sen on luovutettava energiaa fotonin muodossa. Fotonin energia on yhtä suuri kuin näiden kahden radan välinen energiaero, ja fotonin energia saa aikaan sen, että sillä on tietty taajuus ja väri. Bohrin teoria tarjosi hyvän selityksen monille subatomisten ilmiöiden näkökohdille, mutta se ei pystynyt vastaamaan siihen, miksi jokaisella hehkuvan vedyn (ja hehkuvan neonin tai minkä tahansa muun alkuaineen) tuottaman valon värillä on oma kirkkautensa ja miksi kirkkauserot ovat aina samat jokaisella alkuaineella.

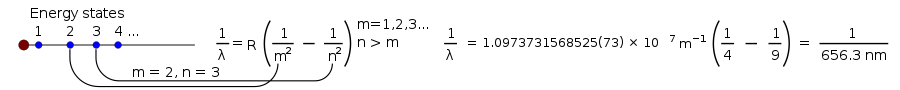
Kun Niels Bohr esitteli teoriansa, suurin osa vetylamppujen tuottamasta valosta oli jo tiedossa, mutta tutkijat eivät vieläkään pystyneet selittämään hehkuvan vedyn tuottamien viivojen kirkkautta.

Werner Heisenberg otti tehtäväkseen selittää jokaisen viivan kirkkauden tai "intensiteetin". Hän ei voinut käyttää mitään yksinkertaista sääntöä, jollaisen Balmer oli keksinyt. Hänen oli käytettävä klassisen fysiikan hyvin vaikeaa matematiikkaa, jossa kaikki lasketaan esimerkiksi elektronin massan (painon), varauksen (staattisen sähkövoiman) ja muiden pienten suureiden avulla. Klassisella fysiikalla oli jo vastauksia vetylamppujen tuottamien värikaistojen kirkkauteen, mutta klassisen teorian mukaan sateenkaaren pitäisi olla jatkuva eikä neljä erillistä värikaistaa. Heisenbergin selitys on:

On olemassa jokin laki, joka sanoo, mitä valotaajuuksia hehkuva vety tuottaa. Sen on ennustettava, että taajuudet ovat hajallaan toisistaan, kun elektronit liikkuvat atomin ytimen (keskuksen) lähellä olevien ratojen välillä, mutta sen on myös ennustettava, että taajuudet lähenevät toisiaan yhä enemmän, kun tarkastelemme, mitä elektroni tekee siirtyessään yhä kauempana olevien ratojen välillä. Sen on myös ennustettava, että taajuuksien väliset intensiteettierot tulevat yhä lähemmäksi toisiaan, kun menemme ulospäin. Siinä missä klassinen fysiikka jo antaa oikeat vastaukset yhdellä yhtälösarjalla, uuden fysiikan on annettava samat vastaukset mutta eri yhtälöillä.

Klassinen fysiikka käyttää Joseph Fourierin matemaattisia menetelmiä matemaattisen kuvan luomiseen fyysisestä maailmasta, Se käyttää kokoelmia sileitä käyriä, jotka menevät yhteen ja muodostavat yhden sileän käyrän, joka antaa tässä tapauksessa kaikkien taajuuksien valon voimakkuudet jostain valosta. Mutta se ei ole oikein, koska tuo sileä käyrä näkyy vain korkeammilla taajuuksilla. Alemmilla taajuuksilla on aina yksittäisiä pisteitä, eikä mikään yhdistä pisteitä. Jotta Heisenberg voisi laatia kartan todellisesta maailmasta, hänen oli tehtävä suuri muutos. Hänen oli tehtävä jotakin poimiakseen vain ne luvut, jotka vastaisivat luonnossa nähtyä. Joskus sanotaan, että hän "arveli" näitä yhtälöitä, mutta hän ei tehnyt sokeita arvauksia. Hän löysi sen, mitä tarvitsi. Hänen laskemansa luvut asettaisivat pisteitä kuvaajaan, mutta pisteiden väliin ei piirrettäisi viivaa. Ja yhden "kuvaajan" tekeminen vain pisteistä jokaista laskentasarjaa varten olisi tuhlannut paljon paperia, eikä sillä olisi saatu mitään aikaan. Heisenberg löysi keinon ennustaa tehokkaasti eri taajuuksien intensiteetit ja järjestää nämä tiedot hyödyllisellä tavalla.

Käyttämällä edellä esitettyä empiiristä sääntöä, jonka Balmer aloitti ja Rydberg paransi, voimme nähdä, miten saamme yhden numerosarjan, joka auttaisi Heisenbergiä saamaan haluamansa kuvan:

Säännön mukaan elektronin siirtyessä kiertoradalta toiselle se joko voittaa tai menettää energiaa riippuen siitä, onko se siirtymässä kauemmas keskuksesta vai lähemmäs sitä. Voimme siis sijoittaa nämä kiertoradat tai energiatasot ruudukon ylä- ja sivupuolelle otsikoiksi. Historiallisista syistä alimman radan nimi on n, ja seuraavaksi ulomman radan nimi on n - a, sitten tulee n - b ja niin edelleen. On hämmentävää, että he käyttivät negatiivisia numeroita, kun elektronit itse asiassa saivat energiaa, mutta niin se vain on.

Koska Rydbergin sääntö antaa meille taajuudet, voimme käyttää tätä sääntöä numeroiden asettamiseen sen mukaan, mihin elektroni menee. Jos elektroni alkaa paikasta n ja päätyy paikkaan n, se ei ole oikeastaan mennyt minnekään, joten se ei ole saanut energiaa eikä menettänyt energiaa. Taajuus on siis 0. Jos elektroni lähtee liikkeelle pisteestä n-a ja päätyy pisteeseen n, se on pudonnut korkeammalta radalta alemmalle radalle. Silloin se menettää energiaa, ja menetetty energia näkyy fotonina. Fotonilla on tietty energiamäärä e, ja se liittyy tiettyyn taajuuteen f yhtälöllä e = h f. Tiedämme siis, että tietty muutos kiertoradalla tuottaa tietyn valotaajuuden f. Jos elektroni alkaa n:stä ja päätyy n-a:han, se on siirtynyt alemmalta kiertoradalta ylemmälle kiertoradalle. Tämä tapahtuu vain, kun ulkopuolelta tulee tietyn taajuuden ja energian omaava fotoni, joka absorboituu elektroniin ja antaa sille energiaa, ja se saa elektronin siirtymään korkeammalle kiertoradalle. Jotta kaikessa olisi järkeä, kirjoitamme taajuuden negatiivisena lukuna. Oli olemassa fotoni, jolla oli tietty taajuus, ja nyt se on otettu pois.

Voimme siis tehdä tällaisen ruudukon, jossa f(a←b) tarkoittaa taajuutta, joka liittyy elektronin siirtymiseen energiatilasta (kiertoradalta) b energiatilaan a. (Jälleen kerran järjestykset näyttävät takaperoisilta, mutta ne on alun perin kirjoitettu näin.):

Ruutu f

Elektronitilat

n

n-a

n-b

n-c

....

n

f(n←n)

f(n←n-a)

f(n←n-b)

f(n←n-c)

.....

n-a

f(n-a←n)

f(n-a←n-a)

f(n-a←n-b)

f(n-a←n-c)

.....

n-b

f(n-b←n)

f(n-b←n-a)

f(n-b←n-b)

f(n-b←n-c)

.....

siirtyminen....

.....

.....

.....

.....

Heisenberg ei tehnyt tällaisia verkkoja. Hän teki vain laskutoimitukset, joiden avulla hän sai etsimänsä intensiteetit. Mutta sitä varten hänen oli kerrottava kaksi amplitudia (kuinka korkea aalto on) saadakseen intensiteetin. (Klassisessa fysiikassa intensiteetti on yhtä suuri kuin amplitudin neliö.) Hän laati oudon näköisen yhtälön tätä ongelmaa varten, kirjoitti loput paperistaan, antoi sen pomolleen ja lähti lomalle. Tohtori Born katsoi hänen outoa yhtälötään, ja se vaikutti hieman hullulta. Hän varmaan ihmetteli: "Miksi Heisenberg antoi minulle tämän oudon jutun? Miksi hänen on tehtävä se näin?" Sitten hän tajusi, että hän katseli suunnitelmaa jostakin, jonka hän jo tiesi hyvin. Hän oli tottunut kutsumaan matriisiksi sitä ruudukkoa tai taulukkoa, jonka pystyimme kirjoittamaan tekemällä esimerkiksi kaikki matemaattiset laskutoimitukset taajuuksille. Ja Heisenbergin outo yhtälö oli sääntö, jolla kaksi niistä kerrotaan keskenään. Max Born oli hyvin, hyvin hyvä matemaatikko. Hän tiesi, että koska kaksi matriisia (ruudukkoa), jotka kerrotaan, edustavat eri asioita (kuten esimerkiksi sijaintia (x,y,z) ja impulssia (mv)), niin kun kerrotaan ensimmäinen matriisi toisella, saadaan yksi vastaus ja kun kerrotaan toinen matriisi ensimmäisellä, saadaan toinen vastaus. Vaikka hän ei tiennytkään matriisimatematiikasta, Heisenberg näki jo tämän "eri vastausten" ongelman ja se oli vaivannut häntä. Mutta tohtori Born oli niin hyvä matemaatikko, että hän näki, että ensimmäisen ja toisen matriisikertolaskun erotus oli aina Planckin vakio h kerrottuna negatiivisen ykkösen neliöjuurella i. Niinpä muutamassa päivässä Heisenbergin löydöstä heillä oli jo perusmatematiikka sille, mitä Heisenberg kutsui mielellään "epämääräisyysperiaatteeksi". Määräämättömyydellä Heisenberg tarkoitti sitä, että elektronin kaltaista asiaa ei vain pystytä määrittämään, ennen kuin se saadaan määritettyä. Se on vähän kuin meduusa, joka on aina ympäriinsä ja joka ei voi olla "paikallaan", ellei sitä tapeta. Myöhemmin ihmiset alkoivat kutsua sitä "Heisenbergin epävarmuusperiaatteeksi", mikä sai monet ihmiset tekemään sen virheen, että he luulivat elektronien ja muiden vastaavien asioiden todella olevan "jossain", mutta me vain olemme epävarmoja siitä omassa mielessämme. Tämä ajatus on väärä. Heisenberg ei puhunut siitä. Ongelmat jonkin asian mittaamisessa ovat ongelma, mutta se ei ole se ongelma, josta Heisenberg puhui.

Heisenbergin ajatusta on hyvin vaikea ymmärtää, mutta voimme selventää sitä esimerkin avulla. Aluksi alamme kutsua näitä ristikoita "matriiseiksi", koska pian meidän on puhuttava matriisien kertolaskusta.

Oletetaan, että meillä on aluksi kahdenlaisia mittaustuloksia, sijainti (q) ja impulssi (p). Vuonna 1925 Heisenberg kirjoitti tällaisen yhtälön:

Y(n,n-b)=\sum _{{a}}^{{}}\,p(n,n-a)q(n-a,n-b) (Yhtälö konjugoituneille muuttujille impulssi ja sijainti)

Hän ei tiennyt sitä, mutta tämä yhtälö antaa mallin kahden matriisin (ruudukon) kirjoittamiseen ja niiden kertomiseen. Säännöt yhden matriisin kertomiseen toisella ovat hieman sotkuiset, mutta tässä on kaksi matriisia mallin mukaan ja niiden tulo:

Matriisi p

Elektronitilat

n-a

n-b

n-c

....

n

p(n←n-a)

p(n←n-b)

p(n←n-c)

.....

n-a

p(n-a←n-a)

p(n-a←n-b)

p(n-a←n-c)

.....

n-b

p(n-b←n-a)

p(n-b←n-b)

p(n-b←n-c)

.....

siirtyminen....

.....

.....

.....

.....

q:n matriisi

Elektronitilat

n-b

n-c

n-d

....

n-a

q(n-a←n-b)

q(n-a←n-c)

q(n-a←n-d)

.....

n-b

q(n-b←n-b)

q(n-b←n-c)

q(n-b←n-d)

.....

n-c

q(n-c←n-b)

q(n-c←n-c)

q(n-c←n-d)

.....

siirtyminen....

.....

.....

.....

.....

Edellä mainittujen kahden matriisin tulon matriisi on Heisenbergin vuonna 1925 julkaistun artikkelin asiaa koskevan yhtälön mukaisesti seuraava:

Elektronitilat

n-b

n-c

n-d

.....

n

A

.....

.....

.....

n-a

.....

B

.....

.....

n-b

.....

.....

C

.....

Missä:

A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+......

B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+......

C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+......

ja niin edelleen.

Jos matriisit käännetään toisin päin, saadaan seuraavat arvot:

A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+......
 B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
 C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....

ja niin edelleen.

Huomaa, miten kertolaskun järjestyksen muuttaminen muuttaa asteittain luvut, jotka todellisuudessa kerrotaan.

 

Näkyvä valo, jota hehkuva vety säteilee. (Aallonpituudet nanometreinä.)  Zoom
Näkyvä valo, jota hehkuva vety säteilee. (Aallonpituudet nanometreinä.)  

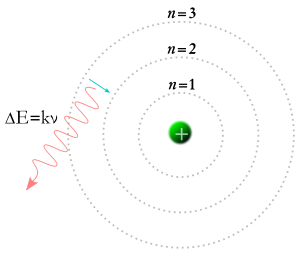
Elektroni putoaa alemmalle radalle ja syntyy fotoni.  Zoom
Elektroni putoaa alemmalle radalle ja syntyy fotoni.  

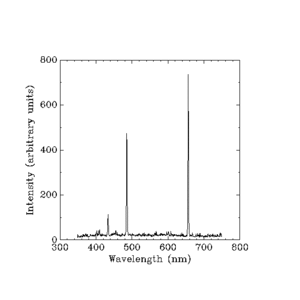
Välilliset intensiteetit mielivaltaisina yksikköinä.  Zoom
Välilliset intensiteetit mielivaltaisina yksikköinä.  

Heisenbergin jälkeen

Werner Heisenbergin työ näytti rikkovan tukoksen. Hyvin pian Louis de Broglien, Max Bornin, Paul Diracin, Wolfgang Paulin ja Erwin Schrödingerin kaltaiset ihmiset kehittivät monia erilaisia tapoja selittää asioita. Kunkin näistä fyysikoista työ on oma tarinansa. Heisenbergin ja aikaisempien ihmisten käyttämää matematiikkaa ei ole kovin vaikea ymmärtää, mutta yhtälöt muuttuivat nopeasti hyvin monimutkaisiksi, kun fyysikot perehtyivät syvällisemmin atomimaailmaan.

 

Muita mysteerejä

Kvanttimekaniikan alkuaikoina Albert Einstein ehdotti, että jos kvanttimekaniikka olisi oikeassa, se merkitsisi, että olisi olemassa "aavemaista toimintaa etäältä". Kävi ilmi, että kvanttimekaniikka olikin oikeassa ja että se, mitä Einstein oli käyttänyt syynä kvanttimekaniikan hylkäämiseen, todella tapahtui. Tällaista "aavemaista yhteyttä" tiettyjen kvanttitapahtumien välillä kutsutaan nykyään "kvanttikietoutumiseksi".

Kun kokeessa kaksi asiaa (fotonit, elektronit jne.) yhdistetään, niillä on oltava yhteinen kvanttimekaaninen kuvaus. Kun ne myöhemmin erotetaan toisistaan, ne säilyttävät saman kvanttimekaanisen kuvauksen tai "tilan". Kaaviossa yksi ominaisuus (esim. "ylös"-spin) on piirretty punaisella ja sen vastine (esim. "alas"-spin) sinisellä. Violetti kaistale tarkoittaa, että kun esimerkiksi kaksi elektronia yhdistetään, parilla on molemmat ominaisuudet. Molemmilla elektroneilla voi siis olla joko ylös- tai alas-spin. Kun ne myöhemmin erotetaan toisistaan, jolloin toinen jää Maahan ja toinen menee jollekin Alpha Centauri -tähden planeetalle, niillä on edelleen kumpikin molemmat spinit. Toisin sanoen kumpikin niistä voi "päättää" näyttää olevansa elektroni, jonka spin on ylös- tai alaspäin. Mutta jos joku myöhemmin mittaa toisen elektronin, sen on "päätettävä" näyttää itsensä vastakkaisen spinin omaavaksi.

Einstein väitti, että oli hullua ajatella, että niin suuren etäisyyden yli yhden elektronin pakottaminen osoittamaan pyörimistä saisi toisen elektronin osoittamaan jotenkin vastakkaista ominaisuutta. Hän sanoi, että molempien elektronien on täytynyt olla koko ajan joko spin-up- tai spin-down-ominaisuuksia, mutta kvanttimekaniikka ei voinut ennustaa, mikä ominaisuus kullakin elektronilla oli. Se, että ei pystynyt ennustamaan, vaan pystyi vain katsomaan toista niistä oikealla kokeella, tarkoitti, että kvanttimekaniikka ei pystynyt selittämään jotakin tärkeää. Siksi kvanttimekaniikassa oli Einsteinin mukaan suuri aukko. Kvanttimekaniikka oli epätäydellinen.

Myöhemmin kävi ilmi, että kokeet osoittivat Einsteinin olleen väärässä.

 

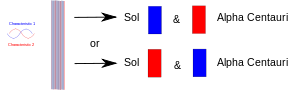
Kaksi toisiinsa kietoutunutta hiukkasta erotetaan toisistaan: toinen on Maassa ja toinen viedään jollekin kaukaiselle planeetalle. Toisen hiukkasen mittaaminen pakottaa sen "päättämään", kumman roolin se ottaa, ja toisen hiukkasen on sitten otettava toinen rooli aina, kun (sen jälkeen) se mitataan.  Zoom
Kaksi toisiinsa kietoutunutta hiukkasta erotetaan toisistaan: toinen on Maassa ja toinen viedään jollekin kaukaiselle planeetalle. Toisen hiukkasen mittaaminen pakottaa sen "päättämään", kumman roolin se ottaa, ja toisen hiukkasen on sitten otettava toinen rooli aina, kun (sen jälkeen) se mitataan.  

Heisenbergin epävarmuusperiaate

Vuonna 1925 Werner Heisenberg kuvasi epävarmuusperiaatteen, jonka mukaan mitä enemmän tiedämme hiukkasen sijainnista, sitä vähemmän voimme tietää, kuinka nopeasti se liikkuu ja mihin suuntaan. Toisin sanoen mitä enemmän tiedämme jonkin pienen asian nopeudesta ja suunnasta, sitä vähemmän voimme tietää sen sijainnista. Fyysikot puhuvat tällaisissa keskusteluissa yleensä vauhdista sen sijaan, että puhuisivat nopeudesta. Momentti on vain jonkin asian nopeus tietyssä suunnassa kertaa sen massa.

Heisenbergin epävarmuusperiaatteen mukaan emme voi koskaan tietää sekä hiukkasen sijaintia että sen liikemäärää. Koska valo on runsas hiukkanen, sitä käytetään muiden hiukkasten mittaamiseen. Ainoa tapa mitata sitä on heijastaa valoaalto hiukkasesta ja tallentaa tulokset. Jos käytetään suurienergistä tai suurtaajuista valonsädettä, voimme kertoa tarkalleen, missä hiukkanen on, mutta emme voi kertoa, kuinka nopeasti se liikkui. Tämä johtuu siitä, että korkeaenerginen fotoni siirtää energiaa hiukkaseen ja muuttaa hiukkasen nopeutta. Jos käytämme matalaenergistä fotonia, voimme kertoa, kuinka nopeasti se liikkuu, mutta emme sitä, missä se on. Tämä johtuu siitä, että käytämme valoa, jonka aallonpituus on pidempi. Pidempi aallonpituus tarkoittaa, että hiukkanen voi olla missä tahansa aallon pituudella.

Periaate sanoo myös, että on olemassa monia mittauspareja, joista emme voi tietää kumpaakaan mistään hiukkasesta (mikä on hyvin pieni asia), vaikka kuinka yrittäisimme. Mitä enemmän opimme tällaisesta parista toisesta, sitä vähemmän voimme tietää toisesta.

Jopa Albert Einsteinilla oli vaikeuksia hyväksyä näin outoa käsitettä, ja tunnetussa keskustelussa hän sanoi: "Jumala ei pelaa noppaa". Tähän tanskalainen fyysikko Niels Bohr vastasi tunnetusti: "Einstein, älä sano Jumalalle, mitä tehdä".

 

Kvanttimekaniikan käyttö

Elektronit ympäröivät jokaisen atomin ydintä. Kemialliset sidokset yhdistävät atomit molekyyleiksi. Kemiallinen sidos yhdistää kaksi atomia, kun atomien välillä jaetaan elektroneja. Kvanttimekaniikka on siis kemiallisen sidoksen ja kemian fysiikkaa. Kvanttimekaniikka auttaa meitä ymmärtämään, miten molekyylit syntyvät ja mitkä ovat niiden ominaisuudet.

Kvanttimekaniikka voi myös auttaa meitä ymmärtämään suuria asioita, kuten tähtiä ja jopa koko maailmankaikkeutta. Kvanttimekaniikka on erittäin tärkeä osa maailmankaikkeuden alkua koskevaa teoriaa, jota kutsutaan alkuräjähdykseksi.

Kaikki aineesta koostuva aine vetää puoleensa toista ainetta painovoimaksi kutsutun perusvoiman vuoksi. Einsteinin teoriaa, joka selittää painovoiman, kutsutaan yleiseksi suhteellisuusteoriaksi. Nykyaikaisen fysiikan ongelmana on, että jotkin kvanttimekaniikan johtopäätökset eivät näytä sopivan yhteen yleisen suhteellisuusteorian kanssa.

Kvanttimekaniikka on fysiikan osa-alue, jolla voidaan selittää, miksi kaikki elektroniikkatekniikka toimii niin kuin se toimii. Näin ollen kvanttimekaniikka selittää tietokoneiden toiminnan, koska tietokoneet ovat elektronisia koneita. Noin 1950-1960-luvun tietokonelaitteistojen suunnittelijoiden ei kuitenkaan tarvinnut ajatella kvanttimekaniikkaa. Myöskään radioiden ja televisioiden suunnittelijat eivät tuolloin ajatelleet kvanttimekaniikkaa. Viime vuosien tehokkaampien integroitujen piirien ja tietokoneiden muistitekniikoiden suunnittelussa tarvitaan kuitenkin kvanttimekaniikkaa.

Kvanttimekaniikka on mahdollistanut myös sellaiset teknologiat kuin:

 

Miksi kvanttimekaniikkaa on vaikea oppia

Kvanttimekaniikka on haastava aihe monesta syystä:

  • Kvanttimekaniikka selittää asioita hyvin eri tavoin kuin se, mitä opimme maailmasta lapsena.
  • Kvanttimekaniikan ymmärtäminen vaatii muutakin matematiikkaa kuin algebraa ja yksinkertaista laskentaa. Se edellyttää myös matriisialgebraa, kompleksilukuja, todennäköisyysteoriaa ja osittaisdifferentiaaliyhtälöitä.
  • Fyysikot eivät ole varmoja siitä, mitä jotkin kvanttimekaniikan yhtälöt kertovat meille todellisesta maailmasta.
  • Kvanttimekaniikan mukaan atomit ja subatomiset hiukkaset käyttäytyvät oudoilla tavoilla, jotka ovat täysin erilaisia kuin mikään, mitä näemme jokapäiväisessä elämässämme.
  • Kvanttimekaniikka kuvaa asioita, jotka ovat äärimmäisen pieniä, joten emme voi nähdä joitakin niistä ilman erikoislaitteita, emmekä monia niistä lainkaan.

Kvanttimekaniikka kuvaa luontoa tavalla, joka poikkeaa siitä, miten yleensä ajattelemme tieteestä. Se kertoo meille, kuinka todennäköistä on, että jotkin asiat tapahtuvat, sen sijaan että se kertoisi, että ne tapahtuvat varmasti.

Yksi esimerkki on Youngin kaksoisrakokeilu. Jos laserilla ammutaan yksittäisiä fotoneja (yksittäisiä valoyksiköitä) valokuvausfilmille, nähdään kehitetyllä filmillä yksittäinen valopiste. Jos laitamme metallilevyn väliin ja teemme levyyn kaksi hyvin kapeaa rakoa, kun ammumme useita fotoneja metallilevyyn ja ne joutuvat kulkemaan rakojen läpi, näemme jotakin merkillistä. Koko kehitetyn kalvon läpi näemme sarjan kirkkaita ja tummia kaistoja. Voimme käyttää matematiikkaa kertoaksemme tarkalleen, missä kirkkaat kaistat ovat ja kuinka kirkasta valo oli, joka aiheutti ne, eli voimme kertoa etukäteen, kuinka monta fotonia osuu kuhunkin kaistaan. Mutta jos hidastamme prosessia ja katsomme, mihin kukin fotoni laskeutuu ruudulla, emme voi koskaan etukäteen tietää, missä seuraava fotoni näkyy. Voimme tietää varmasti, että on todennäköisintä, että fotoni osuu keskimmäiseen kirkkaaseen kaistaan, ja että on yhä epätodennäköisempää ja epätodennäköisempää, että fotoni osuu kaistoille, jotka ovat yhä kauempana keskipisteestä. Tiedämme siis varmasti, että kaistat ovat kirkkaimpia keskellä ja himmenevät yhä kauempana. Mutta emme koskaan tiedä varmasti, mikä fotoni menee millekin kaistalle.

Yksi kvanttimekaniikan teorian oudoista johtopäätöksistä on "Schrödingerin kissa" -ilmiö. Hiukkasen tietyistä ominaisuuksista, kuten sijainnista, liikenopeudesta, liikesuunnasta ja "spinistä", ei voida puhua ennen kuin jokin mittaa ne (esimerkiksi elektronista kimpoava fotoni lasketaan elektronin sijainnin mittaukseksi). Ennen mittausta hiukkanen on "tilojen superpositiossa", jossa sen ominaisuuksilla on useita arvoja samanaikaisesti. Schrödinger sanoi, että kvanttimekaniikka näytti sanovan, että jos jokin asia (kuten kissan elämä tai kuolema) määräytyy kvanttitapahtuman perusteella, sen tila määräytyy kvanttitapahtuman tuloksena syntyneen tilan perusteella, mutta vain sillä hetkellä, kun joku tarkastelee kvanttitapahtuman tilaa. Aikana ennen kuin kvanttitapahtuman tilaa tarkastellaan, ehkä "elävä ja kuollut kissa (anteeksi ilmaisu) [ovat] sekoittuneet tai likaantuneet yhtä suurina osina".

 

Pienennetty Planckin vakio

Ihmiset käyttävät usein symbolia \hbar , jota kutsutaan nimellä "h-bar". \hbar ={\frac {h}{2\pi }} . H-bar on kulmamomentin yksikkö. Kun tätä uutta yksikköä käytetään kuvaamaan atomien elektronien ratoja, minkä tahansa radalla olevan elektronin kulmavauhti on aina kokonaisluku.

 

Esimerkki

Hiukkanen 1-ulotteisessa kuopassa on yksinkertaisin esimerkki siitä, että hiukkasen energialla voi olla vain tiettyjä arvoja. Energian sanotaan olevan "kvantittunut". Kuopan potentiaalienergia on nolla tietyn alueen sisällä ja ääretön potentiaalienergia kaikkialla alueen ulkopuolella. Yksiulotteisessa tapauksessa x suunnassa ajasta riippumaton Schrödingerin yhtälö voidaan kirjoittaa seuraavasti:

-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi .

Differentiaaliyhtälöiden avulla voimme selvittää, että \psi voidaan kirjoittaa muodossa

\psi =Ae^{{ikx}}+Be^{{-ikx}}\;\;\;\;\;\;E={\frac {\hbar ^{2}k^{2}}{2m}}

tai kuten

\psi =C\sin kx+D\cos kx\; (Eulerin kaavalla).

Laatikon seinät tarkoittavat, että aaltofunktiolla on oltava erityinen muoto. Hiukkasen aaltofunktion on oltava nolla aina, kun seinät ovat äärettömän korkeita. Jokaisella seinällä:

\psi =0\;{\mathrm {at}}\;\;x=0,\;x=L

Tarkastellaan x = 0

  • sin 0 = 0, cos 0 = 1. Jotta täyttyisi {\displaystyle \psi =0\;} cos-termi on poistettava. Näin ollen D = 0

Mieti nyt: {\displaystyle \psi =C\sin kx\;}

  • {\displaystyle x=L} {\displaystyle \psi =C\sin kL=0\;}
  • Jos {\displaystyle C=0} niin {\displaystyle \psi =0\;} kaikille x. Tämä ratkaisu ei ole hyödyllinen.
  • joten {\displaystyle \sin kL=0} on oltava tosi, jolloin saadaan

kL=n\pi \;\;\;\;n=1,2,3,4,5,...\;

Näemme, että n on oltava kokonaisluku. Tämä tarkoittaa, että hiukkasella voi olla vain erityisiä energia-arvoja, eikä sillä voi olla energia-arvoja siltä väliltä. Tämä on esimerkki energian "kvantittumisesta".

 

Aiheeseen liittyvät sivut

 

Lisää lukemista
  • Cox, Brian; & Forshaw, Jeff (2011). Kvanttiuniversumi: Everything That Can Happen Does Happen. Allen Lane. ISBN 978-1-84614-432-5.

 

Kysymyksiä ja vastauksia

Kysymys: Mitä on kvanttimekaniikka?


V: Kvanttimekaniikka on fysiikan osa-alue, joka selittää, miten maailmankaikkeus toimii atomeja pienemmässä mittakaavassa. Se tunnetaan myös nimellä kvanttifysiikka tai kvanttiteoria.

K: Mitä termi "kvantti" tarkoittaa?


V: Termi "kvantti" tulee latinasta ja tarkoittaa "kuinka paljon". Energiakvantti on pienin mahdollinen määrä (tai pienin ylimääräinen määrä), ja kvanttimekaniikka kuvaa, miten tämä energia liikkuu tai on vuorovaikutuksessa.

K: Mitä ovat subatomiset hiukkaset?


V: Subatomiset hiukkaset ovat hiukkasia, jotka muodostavat atomeja, kuten protonit, neutronit ja elektronit. Ne ovat jopa pienempiä kuin atomit.

K: Miten kvanttimekaniikka kuvaa näiden hiukkasten toimintaa?


V: Kvanttimekaniikka tarjoaa matemaattiset säännöt, joiden avulla voidaan tutkia subatomisia hiukkasia ja sähkömagneettisia aaltoja, jotta voidaan ymmärtää niiden käyttäytymistä ja vuorovaikutusta toistensa kanssa.

K: Mitä on aalto-hiukkasdualismi?


V: Aalto-hiukkasdualismi viittaa siihen, että sekä hiukkaset että aallot voivat käyttäytyä toistensa tavoin - ne eivät ole kaksi erillistä olentoa, vaan pikemminkin jotain molempia yhdistettynä yhdeksi ilmiöksi.

K: Miten modernia fysiikkaa voidaan kuvata kvanttimekaniikan avulla?


V: Nykyaikainen fysiikka ja kemia voidaan selittää soveltamalla niihin kvanttimekaniikan matemaattisia sääntöjä.

AlegsaOnline.com - 2020 / 2023 - License CC3