Trigonometria: kulmat, kolmiot ja trigonometriset funktiot

Trigonometria: kulmat, kolmiot ja trigofunktiot (sin, cos, tan) — ytimekäs opas, selkeät kaavat ja käytännön esimerkit opiskelijoille ja harrastajille.

Tekijä: Leandro Alegsa

20-03-2026 14:05

Trigonometria (kreikan sanoista trigonon = kolme kulmaa ja metron = mitta) on matematiikan alkeisosa, joka käsittelee kulmia, kolmioita ja trigonometrisia funktioita, kuten siniä (lyhenne sin), kosinia (lyhenne cos) ja tangenttia (lyhenne tan). Sillä on jonkinlainen yhteys geometriaan, vaikka siitä, mikä tämä yhteys tarkalleen ottaen on, vallitsee erimielisyyttä; joidenkin mielestä trigonometria on vain osa geometriaa.

Kulmat ja mittayksiköt

Kulmat mitataan yleisimmin asteina (°) ja radianein (rad). Yksi täysi ympyrä on 360° tai 2π rad. Muunnos asteista radiaaneiksi on rad = aste × π/180, ja toisinpäin aste = rad × 180/π. Kulmien suunta voi olla positiivinen (yleensä vastapäivään) tai negatiivinen (myötäpäivään).

Kolmiot ja perusmääritelmät

Trigonometria alkaa usein suorakulmaisen kolmion käsittelystä. Merkitään suorakulmaisen kolmion kulmia A, B ja C siten, että C on 90°. Kulmaa A vastapäätä oleva sivu on vastainen (opp), viereinen ei-hypotenuusa on viereinen (adj) ja pisin sivu on hypotenuusa (hyp).

sin A = vastainen / hypotenuusa
cos A = viereinen / hypotenuusa
tan A = vastainen / viereinen = sin A / cos A

Nämä suhteet pätevät myös yleisemmin yksikköympyrän avulla (ks. alla).

Yksikköympyrä

Yksikköympyrä on ympyrä, jonka säde on 1 ja keskipiste on origossa. Kulman a kohtaan yksikköympyrällä liittyy piste (cos a, sin a):

cos a on pisteen x-koordinaatti
sin a on pisteen y-koordinaatti
tan a on y/x, kun x ≠ 0

Tämä näkemys selittää trigonometristen funktioiden jaksollisuuden ja merkkimuutokset kulman neljänneksissä. Funktioilla on perusperiodi 2π: esimerkiksi sin(a + 2π) = sin a.

Muita trigonometrisia funktioita ja käänteiset funktiot

Perusfunktioiden lisäksi usein käytetään niiden käänteis- ja käänteispuolitoimisia funktioita:

sec a = 1 / cos a (sekantti)
csc a = 1 / sin a (kosekantti)
cot a = 1 / tan a = cos a / sin a (kotangenssi)
arcsin, arccos, arctan ovat käänteisiä funktioita, jotka antavat kulman tietystä arvosta. Niillä on määrittelyalueet ja raja-arvot, esim. arcsin antaa tuloksia välillä [−π/2, π/2].

Tärkeitä identiteettejä ja kaavoja

Useita kaavoja on hyvä osata:

Pythagoraan identiteetti: sin^2 a + cos^2 a = 1
Summa- ja erotuskaavat:
- sin(a ± b) = sin a cos b ± cos a sin b
- cos(a ± b) = cos a cos b ∓ sin a sin b
- tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a tan b)
Kaksoiskulma:
- sin 2a = 2 sin a cos a
- cos 2a = cos^2 a − sin^2 a = 1 − 2 sin^2 a = 2 cos^2 a − 1

Kolmion ratkaiseminen

Kun tiedetään kulmia ja sivuja, trigonometria auttaa ratkaisemaan kolmion kokonaan.

Sinilause: a / sin A = b / sin B = c / sin C. Tätä käytetään, kun tiedetään esim. kaksi kulmaa ja yksi sivu tai kaksi sivua ja kulma ei sivujen välissä.
Kosinilause: c^2 = a^2 + b^2 − 2ab cos C. Tätä käytetään, kun tiedetään kaksi sivua ja niiden välinen kulma tai kaikki kolme sivua.

Käytännön esimerkkejä

Perusesimerkkejä: sin 30° = 1/2, cos 60° = 1/2 ja tan 45° = 1. Asteen muuntaminen radiaaneiksi: 30° = π/6 rad (koska 30 × π/180 = π/6).

Sovellukset

Trigonometria on keskeinen monilla aloilla:

kartoitus ja navigointi (suunnan ja etäisyyden laskeminen)
rakennus- ja koneinsinöörityö (voimat, kulmat, rakenteiden mitoitus)
fysiikka (aallot, värähtelyt, optiikka)
signaalinkäsittely ja Fourier-analyysi (aaltomuotojen dekompositio sinikäyriksi)
tietokonegrafiikka (rotaatiot ja projektioiden laskenta)

Lyhyt historiallinen huomio

Sana tulee kreikan sanoista trigonon ja metron, kuten edellä mainittu. Trigonometria on kehittynyt antiikin tähtitieteellisistä tarpeista ja myöhemmin vakiintunut osaksi sekä analyysiä että geometrista ajattelua.

Jos haluat, voin lisätä piirroksia, esimerkkilaskuja tai tehdä lyhyen harjoitustehtäväsarjan eri vaikeustasoille.

Yleiskatsaus ja määritelmät

Trigonometriassa käytetään monia erityisiä sanoja kuvaamaan kolmion osia. Joitakin trigonometrian määritelmiä ovat:

Suorakulmainen kolmio - Suorakulmainen kolmio on kolmio, jonka kulma on 90 astetta. (Kolmio voi olla vain yksi suorakulmainen.) Tavallisia trigonometrisia suhdelukuja voidaan käyttää vain suorakulmaisiin kolmioihin.
Hypotenuusa - Kolmion hypotenuusa on kolmion pisin sivu ja se sivu, joka on vastapäätä suorakulmaa. Esimerkiksi oikealla olevan kolmion hypotenuusa on sivu c.
Kulman vastakkainen puoli - Kulman vastakkainen puoli on se puoli, joka ei leikkaa kulman kärkeä. Esimerkiksi sivu a on oikealla olevan kolmion kulman A vastakohta.
Kulman vierekkäinen sivu - Kulman vierekkäinen sivu on sivu, joka leikkaa kulman kärkipisteen, mutta ei ole hypotenuusa. Esimerkiksi sivu b on oikealla olevan kolmion kulman A vieressä.

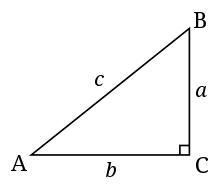
Tavallinen suorakulmainen kolmio. C on suorakulma tässä kuvassa

Trigonometriset suhteet

Suorakulmaisille kolmioille on kolme tärkeintä trigonometrista suhdelukua ja kolme näiden suhdelukujen käänteislukua. Yhteensä suhdelukuja on 6. Ne ovat:

Sinus (sin) - Kulman sini on yhtä suuri kuin vastakkainen hypotenuusa {\displaystyle {{\text{Opposite}} \over {\text{Hypotenuusa}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Kosinus (cos) - Kulman kosinus on yhtä suuri kuin vierekkäisen hypotenuusan {\displaystyle {{\text{Adjacent}} \over {\text{Hypotenuusa}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangentti (tan) - Kulman tangentti on yhtä suuri kuin vastakkainen vierekkäinen {\displaystyle {{\text{Opposite}} \over {\text{Adjacent}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

Näiden suhdelukujen käänteisluvut ovat:

Kosecantti (csc) - Kulman kosecantti on yhtä suuri kuin hypotenuusan vastakohta {\displaystyle {{\text{Hypotenuusa}} \over {\text{Opposite}}}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ tai csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \over \sin \theta}} $\csc \theta ={1 \over \sin \theta }$

Sekantti (sec) - Kulman sekantti on yhtä suuri kuin hypotenuusan vierekkäinen {\displaystyle {{\text{Hypotenuusa}} \over {\text{Adjacent}}}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ tai sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \over \cos \theta }} $\sec \theta ={1 \over \cos \theta }$

Cotangentti (cot) - Kulman cotangentti on yhtä suuri kuin vierekkäinen vastakkainen {\displaystyle {{\text{Adjacent}} \over {\text{Opposite}}}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ tai cot θ = 1 tan θ {\displaystyle \cot \theta ={1 \over \tan \theta}} $\cot \theta ={1 \over \tan \theta }$

Opiskelijat käyttävät usein muistisääntöjä tämän suhteen muistamiseksi. Suorakulmaisen kolmion sini-, kosini- ja tangenttisuhteet voidaan muistaa esittämällä ne kirjainjonoina, kuten SOH-CAH-TOA:

Sinus = vastakkainen ÷ hypotenuusa

Kosinus = vierekkäinen ÷ hypotenuusa

Tangentti = vastakkainen ÷ vierekkäinen

Käyttämällä trigonometriaa

Sinien ja kosinusten avulla voi vastata lähes kaikkiin kolmioita koskeviin kysymyksiin. Tätä kutsutaan kolmion "ratkaisemiseksi". Minkä tahansa kolmion loput kulmat ja sivut voidaan selvittää heti, kun tiedetään kaksi sivua ja niihin sisältyvä kulma tai kaksi kulmaa ja yksi sivu tai kolme sivua. Nämä lait ovat käyttökelpoisia kaikilla geometrian aloilla, koska jokainen monikulmio voidaan kuvata kolmioiden yhdistelmänä.

Trigonometria on tärkeää myös maanmittauksessa, vektorianalyysissä ja jaksollisten funktioiden tutkimisessa.

On olemassa myös niin sanottu pallotrigonometria, joka käsittelee pallogeometriaa. Sitä käytetään tähtitieteen, geodesian ja navigoinnin laskelmissa.

Trigonometrian lait

Sinusten laki

a Sin A = b Sin B = c Sin C {\displaystyle {\displaystyle {\text{a}} \over {\text{Sin A}}={\text{b}} \over {\text{Sin B}}={\text{c}} \over {\text{Sin C}}}}} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Kosinusten laki

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Tangenttien laki

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}}(A+B))}}} ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$

Etsiä