Matematiikka

Matematiikka on lukujen, muotojen ja kuvioiden tutkimusta. Sana tulee kreikan kielen sanasta μάθημα (máthema), joka tarkoittaa "tiedettä, tietoa tai oppimista", ja se lyhennetään joskus sanoiksi maths (Englannissa, Australiassa, Irlannissa ja Uudessa-Seelannissa) tai math (Yhdysvalloissa ja Kanadassa). Oppilaat ja heidän koulunsa käyttävät usein lyhennettyjä sanoja aritmetiikasta, geometriasta tai yksinkertaisesta algebrasta.

Matematiikkaan kuuluu seuraavien aineiden opiskelu:

Numerot: miten asioita voidaan laskea.
Rakenne: miten asiat on järjestetty. Tätä osa-aluetta kutsutaan yleensä algebraksi.
Paikka: missä asiat ovat ja miten ne on järjestetty. Tätä osa-aluetta kutsutaan yleensä geometriaksi.
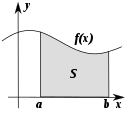
Muutos: miten asiat muuttuvat erilaisiksi. Tätä osa-aluetta kutsutaan yleensä analyysiksi.

Matematiikasta on hyötyä reaalimaailmassa esiintyvien ongelmien ratkaisemisessa, joten monet muutkin kuin matemaatikot opiskelevat ja käyttävät matematiikkaa. Nykyään matematiikkaa tarvitaan jonkin verran monissa työtehtävissä. Liiketoiminnan, luonnontieteiden, tekniikan ja rakentamisen parissa työskentelevät ihmiset tarvitsevat jonkin verran matematiikan osaamista.

Matematiikan ongelmanratkaisu

Matematiikka ratkaisee ongelmia logiikan avulla. Yksi matemaatikkojen käyttämistä logiikan tärkeimmistä työkaluista on päättely. Deduktio on erityinen ajattelutapa, jolla löydetään ja todistetaan uusia totuuksia vanhojen totuuksien avulla. Matemaatikolle syy siihen, miksi jokin on totta (jota kutsutaan todisteeksi), on yhtä tärkeä kuin se, että se on totta, ja tämä syy löydetään usein deduktion avulla. Johtopäätösten käyttäminen erottaa matemaattisen ajattelun muunlaisesta tieteellisestä ajattelusta, joka saattaa nojautua kokeisiin tai haastatteluihin.

Matemaatikot käyttävät logiikkaa ja päättelyä luodakseen yleisiä sääntöjä, jotka ovat tärkeä osa matematiikkaa. Näissä säännöissä jätetään pois tietoja, jotka eivät ole tärkeitä, jotta yksi sääntö voi kattaa monia tilanteita. Löytämällä yleisiä sääntöjä matematiikka ratkaisee monia ongelmia samaan aikaan, kun näitä sääntöjä voidaan käyttää muihin ongelmiin. Näitä sääntöjä voidaan kutsua teoreemoiksi (jos ne on todistettu) tai arvauksiksi (jos ei vielä tiedetä, ovatko ne totta). Useimmat matemaatikot käyttävät ei-loogista ja luovaa päättelyä löytääkseen loogisen todistuksen.

Joskus matematiikka löytää ja tutkii sääntöjä tai ideoita, joita emme vielä ymmärrä. Usein matematiikassa ideat ja säännöt valitaan, koska niitä pidetään yksinkertaisina tai siisteinä. Toisaalta joskus nämä ideat ja säännöt löytyvät reaalimaailmasta sen jälkeen, kun niitä on tutkittu matematiikassa; näin on tapahtunut monta kertaa aiemmin. Yleisesti ottaen matematiikan sääntöjen ja ideoiden tutkiminen voi auttaa meitä ymmärtämään maailmaa paremmin. Esimerkkejä matematiikan ongelmista ovat yhteen- ja vähennyslasku, kertolasku, jakolasku, laskutoimitukset, murtoluvut ja desimaaliluvut. Algebraongelmat ratkaistaan arvioimalla tiettyjä muuttujia. Laskin vastaa jokaiseen matemaattiseen ongelmaan neljällä aritmeettisella perusoperaatiolla.

Matematiikan opintoalat

Numero

Matematiikka käsittää lukujen ja määrien tutkimuksen.Se on tieteenala, joka käsittelee muodon, määrän ja järjestelyn logiikkaa. Useimpia alla luetelluista alueista tutkitaan monilla eri matematiikan aloilla, kuten joukko-opissa ja matemaattisessa logiikassa. Lukuteorian tutkimuksessa keskitytään yleensä enemmän kokonaislukujen rakenteeseen ja käyttäytymiseen kuin itse lukujen varsinaisiin perusteisiin, joten sitä ei ole lueteltu tässä alaluvussa.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0.125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0.125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Luonnolliset luvut	Kokonaisluvut	Rationaaliluvut	Reaaliluvut	Kompleksiluvut
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} $f(x)={\sqrt {x}}$
Järjestysluvut	Kardinaalinumerot	Aritmeettiset operaatiot	Aritmeettiset suhteet	Toiminnot

Rakenne

Monilla matematiikan osa-alueilla tutkitaan kohteen rakennetta. Useimmat näistä alueista ovat osa algebran tutkimusta.


Lukuteoria	Abstrakti algebra	Lineaarialgebra	Järjestyksen teoria	Graafiteoria

Muoto

Joillakin matematiikan osa-alueilla tutkitaan asioiden muotoja. Useimmat näistä alueista ovat osa geometrian tutkimusta.


Topologia	Geometria	Trigonometria	Differentiaaligeometria	Fraktaaligeometria

Muuta

Joillakin matematiikan osa-alueilla tutkitaan sitä, miten asiat muuttuvat. Useimmat näistä alueista ovat osa analyysin tutkimusta.


Calculus	Vektorilaskenta	Analyysi

Differentiaaliyhtälöt	Dynaamiset järjestelmät	Kaaosteoria

Sovellettu matematiikka

Sovelletussa matematiikassa käytetään matematiikkaa muiden alojen, kuten tekniikan, fysiikan ja tietojenkäsittelyn, ongelmien ratkaisemiseen.

Numeerinen analyysi - Optimointi - Todennäköisyysteoria - Tilastotiede - Matemaattinen rahoitus - Peliteoria - Matemaattinen fysiikka - Fluiddynamiikka - Laskennalliset algoritmit

Kuuluisia teoreemoja

Nämä teoreemat ovat kiinnostaneet matemaatikkoja ja ihmisiä, jotka eivät ole matemaatikkoja.

Pythagoraan lause - Fermat'n viimeinen lause - Goldbachin arvelu - Twin Prime Conjecture - Gödelin epätäydellisyysteoreema - Poincarén arvelu - Cantorin diagonaaliargumentti - Neljän värin lause - Zornin lemma - Eulerin identiteetti - Church-Turingin teesi.

Nämä ovat teoreemoja ja arvauksia, jotka ovat muuttaneet matematiikkaa suuresti.

Riemannin hypoteesi - Jatkuvuushypoteesi - P Versus NP - Pythagoraan lause - Keskeinen raja-arvoteoria - Laskennan perustava lause - Algebran perustava lause - Aritmeettisen laskennan perustava lause - Projektionaalisen geometrian perustava lause - Pintojen luokitteluteoriat - Gauss-Bonnet'n lause - Fermat'n viimeinen lause - Kantorovitshin lause.

Perusteet ja menetelmät

Matematiikan luonteen ymmärtämisessä tapahtunut edistys vaikuttaa myös siihen, miten matemaatikot opiskelevat aihettaan.

Matematiikan filosofia - Matemaattinen intuitionismi - Matemaattinen konstruktivismi - Matematiikan perusteet - Joukko-oppi - Symbolinen logiikka - Mallioppi - Kategoriateoria - Logiikka - Käänteismatematiikka - Matemaattisten symbolien taulukko - Matemaattisten symbolien taulukko

Historia ja matemaatikkojen maailma

Matematiikka historiassa ja matematiikan historia.

Matematiikan historia - Matematiikan aikajana - Matemaatikot - Fields-mitali - Abel-palkinto - Millennium Prize Problems (Clay MathPrize) - Kansainvälinen matemaattinen liitto - Matematiikkakilpailut - Sivuttaisajattelu - Matematiikka ja sukupuoli.

Matematiikan palkinnot

Matematiikan Nobel-palkintoa ei ole olemassa. Matemaatikot voivat saada Abel-palkinnon ja Fields-mitalin merkittävistä teoksista.

Clay Mathematics Institute on ilmoittanut antavansa miljoona dollaria sille, joka ratkaisee yhden vuosituhannen vaihteen palkinto-ongelmista.

Matemaattiset työkalut

Matematiikan tekemiseen tai vastausten löytämiseen matematiikan ongelmiin käytetään monia välineitä.

Vanhemmat työkalut

Abacus
Napierin luut, laskutikku
Viivotin ja kompassi
Psyykkinen laskenta

Uudemmat työkalut

Laskimet ja tietokoneet
Ohjelmointikielet
Tietokonealgebrajärjestelmät (luettelo)
Internetin lyhennemerkintä
tilastoanalyysiohjelmisto (esimerkiksi SPSS)
SAS-ohjelmointikieli
R-ohjelmointikieli

Katso myös

Matematiikan naisten aikajana
American Mathematical Society
Teollisen ja soveltavan matematiikan yhdistys
Matematiikan sukututkimusprojekti
Matematiikan aineluokitus

Kysymyksiä ja vastauksia

Q: Mitä on matematiikka?

V: Matematiikka on lukujen, muotojen ja kuvioiden tutkimusta. Sana tulee kreikan sanasta μάθημα (máthema), joka tarkoittaa "tiedettä, tietoa tai oppimista".

Q: Mitkä ovat matematiikan tärkeimmät osa-alueet?

V: Matematiikan pääalueita ovat luvut, rakenne (algebra), paikka (geometria) ja muutos (analyysi).

K: Miten matematiikkaa käytetään reaalimaailmassa?

V: Sovellettu matematiikka on hyödyllistä reaalimaailman ongelmien ratkaisemisessa. Liiketoiminnassa, tieteessä, tekniikassa ja rakentamisessa työskentelevät ihmiset käyttävät matematiikkaa.

K: Onko "matematiikasta" olemassa lyhennettyä versiota?

V: Kyllä - se voidaan lyhentää muotoon "maths" Brittiläisen kansainyhteisön maissa tai "math" Pohjois-Amerikassa.

K: Mitä sana 'matematiikka' tarkoittaa?

V: Sana "matematiikka" tulee kreikan kielen sanasta μάθημα (máthema), joka tarkoittaa "tiedettä, tietoa tai oppimista".

K: Millaista ongelmanratkaisua soveltava matematiikka sisältää?

V: Sovellettuun matematiikkaan kuuluu sellaisten reaalimaailman ongelmien ratkaiseminen, joita liike-elämän, luonnontieteiden, tekniikan ja rakentamisen parissa työskentelevät ihmiset kohtaavat.