Young–Laplace'n yhtälö: kapillaarinen paine-ero ja pintajännitys
Young–Laplace'n yhtälö selitetty: kapillaarinen paine-ero, pintajännitys ja sovellukset fysiikassa ja fysiologiassa. Lue selkeä matemaattinen kuvaus ja käytännön esimerkit.
Fysiikassa Young–Laplacen yhtälö (/ləˈplɑːs/) on epälineaarinen osittaisdifferentiaaliyhtälö, joka kuvaa kapillaarista paine-eroa kahden staattisen nesteen, kuten veden ja ilman, rajapinnassa. Tämä paine-ero johtuu pinnan tai seinämän jännityksestä (pintajännitys). Yhtälö suhteuttaa paine-eron pinnan muotoon ja on keskeinen staattisten kapillaaripintojen ja pintajännityksen ilmiöiden ymmärtämisessä.
Yksinkertaisimmassa muodossaan Young–Laplacen yhtälö annetaan muotoon
- Δp = γ(1/R1 + 1/R2),
missä Δp on paine-ero pinnan kahden puolen välillä, γ on pintajännitys (yksikkö N/m) ja R1 ja R2 ovat pinnan kaksi pääkaarevuussädettä (principaalikaarevuudet). Tämä tarkoittaa, että paine-ero on verrannollinen pinnan keskimääräiseen kaarevuuteen (mean curvature). Erityistapauksina:
- pyöreälle pisaralle tai kuplalle (pinta on pallonmuotoinen): Δp = 2γ / R,
- pitkälle sylinterille (esim. pitkän ohutputken sisällä oleva kaareva pinta): Δp = γ / R.
Merkitys ja sovelluksia
- kapillaarinen nousu ja lasku putkissa (Jurin laki ja vastaavat ilmiöt),
- pisaroiden ja kuplien muotojen ja stabiilisuuden laskenta,
- saippuakalvot ja emulsiot,
- mikropisaroiden ja nanokoteloiden käyttäytyminen sekä pintavoimien merkitys pienissä mittakaavoissa,
- fysiologiassa käytettynä nimellä Laplacen laki kuvaamaan esimerkiksi verisuonten tai keuhkorakkuloiden (alveolit) sisäistä painetta suhteessa seinämän jännitykseen ja säteeseen — pienemmällä säteellä paine pyrkii olemaan suurempi ellei pintajännitystä vähennetä (esim. keuhkojen pintakirkaste eli surfaktantti).
Periaate ja johtaminen
Yhtälön voi johtaa virtuaalisen työn tai energiaperiaatteen avulla: pienen tilavuuden muutoksen δV aiheuttama työ Δp·δV tulee tasapainoon pinnan muutosenergiasta γ·δA (pinnanenergia γ kertaa pinta-alan muutos δA). Tämä antaa yhteyden paine-eron ja pinnan kaarevuuden välillä. Gaussin johtamistapa käytti myös Bernoullin virtuaalisen työn periaatetta reunaehtoineen.
Signifikaatio ja merkkikonventiot
On tärkeää huomata merkkikonventiot: kaarevuuden merkitys ja se kumpi puoli on "korkeammalla" tai "alhaisemalla" paineella riippuvat siitä, miten kaarevuuden etumerkki määritellään (kumpi suunta katsotaan positiiviseksi). Käytännön laskuissa riittää usein absoluuttinen kaarevuus; fysiologiassa ja mekaniikassa käytetään myös muotoa, joka liittyy seinämän jännitykseen: sylinterille Δp = T / r ja pallolle Δp = 2T / r, missä T on seinämän tai kalvon lineaarinen jännitys (N/m).
Rajoitukset ja laajennukset
- Young–Laplacen yhtälö pätee staattisille (tai kvasi-staattisille) pinnoille, joissa viskoosiset ja inertiaaliset vaikutukset voidaan jättää huomiotta.
- Dynaamisissa tilanteissa täytyy huomioida myös virtauskentät, viskositeetti, Marangoni-ilmiöt (pintajännityksen gradientit) ja pintakemialliset vaikutukset (surfaktantit), jolloin yksinkertainen yhtälö laajennetaan tai korvataan kokonaisemmilla malleilla.
- Pienissä kokoluokissa termodynaamiset vaikutukset, kuten Kelvinin vaikutus höyrystymiseen/tiivistymiseen, voivat muuttaa käytännön käyttäytymistä.
Fysiologiassa se tunnetaan yleisesti nimellä Laplacen laki. Sitä käytetään esimerkiksi kuvaamaan painetta onttojen elinten sisällä ja arvioimaan seinämän jännityksen vaikutusta verisuonissa ja keuhkorakkuloissa. Surfactanttien puute tai epätasainen jakautuminen voi johtaa epästabiiliuteen pienissä keuhkorakkuloissa — ilmiö, joka liittyy hapettomuustiloihin vastasyntyneillä.
Yhtälö on nimetty Thomas Youngin mukaan, joka kehitti pintajännityksen laadullisen teorian vuonna 1805, ja Pierre-Simon Laplacen mukaan, joka sai matemaattisen kuvauksen valmiiksi seuraavana vuonna. Sitä kutsutaan joskus myös Young–Laplace–Gauss-yhtälöksi: Carl Friedrich Gauss yhdisti Youngin ja Laplacen työt vuonna 1830. Gauss johti sekä differentiaaliyhtälön että reunaehdot käyttäen Johann Bernoullin virtuaalisen työn periaatteita.
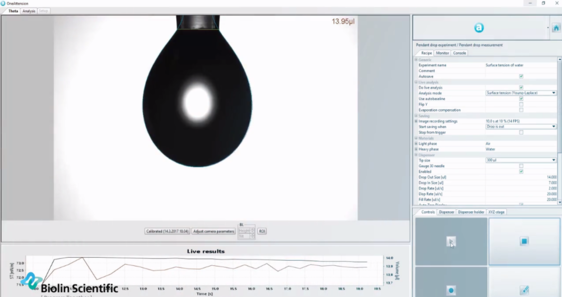
Optiset tensiometrit käyttävät Young-Laplacen yhtälöä nesteen pintajännityksen automaattiseen määrittämiseen pisaran muodon perusteella.
Kysymyksiä ja vastauksia
Q: Mikä on Young-Laplacen yhtälö?
A: Young-Laplacen yhtälö on epälineaarinen osittaisdifferentiaaliyhtälö, joka kuvaa kapillaarista paine-eroa kahden staattisen nesteen, kuten veden ja ilman, rajapinnassa.
K: Mihin se liittyy?
V: Se suhteuttaa paine-eron pinnan tai seinämän muotoon.
K: Kuka kehitti tämän teorian?
V: Teorian kehitti Thomas Young vuonna 1805, ja Pierre-Simon Laplace sai sen matemaattisen kuvauksen valmiiksi seuraavana vuonna. Myöhemmin Carl Friedrich Gauss yhtenäisti sen vuonna 1830.
K: Miten sitä käytetään fysiologiassa?
V: Fysiologiassa se tunnetaan Laplacen lakina, ja sitä käytetään kuvaamaan painetta onttojen elinten sisällä.
K: Mitä ilmiötä se selittää?
V: Young-Laplacen yhtälö selittää pintajännityksen tai seinäjännityksen ilmiön.
K: Sovelletaanko seinäjännitystä paksuihin seinämiin? V: Ei, seinäjännitystä voidaan käyttää vain hyvin ohuille seinämille.
Etsiä