16-soluinen
Neliulotteisessa geometriassa 16-solu on säännöllinen kupera monikulmio eli polytooppi neljässä ulottuvuudessa. Se tunnetaan myös nimellä heksadekachoron. Se on yksi kuudesta säännöllisestä kuperasta monikulmiosta, jotka sveitsiläinen matemaatikko Ludwig Schläfli kuvasi ensimmäisen kerran 1800-luvun puolivälissä.
Conway kutsuu sitä ortopleksiksi ortanttikompleksille, samoin kuin koko ristipolyytooppien luokkaa.
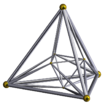
Hexadecachoron
Geometria
Heksadekachoron kuuluu polytooppien perheeseen, jota kutsutaan ristipolytoopeiksi ja joka on olemassa kaikissa ulottuvuuksissa. Sen kaksoispolykhoron on tesserakti (4-ulotteinen hyperkuutio).
Sitä rajoittaa 16 solua, jotka kaikki ovat säännöllisiä tetraedrejä. Siinä on 32 kolmionmuotoista pintaa, 24 reunaa ja 8 kärkeä. 24 reunaa rajoittavat 6 neliötä, jotka sijaitsevat 6 koordinaattitasossa.
Heksadekakoronin kahdeksan kärkeä ovat (±1, 0, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, 0, ±1). Kaikki kärkipisteet ovat yhteydessä toisiinsa särmillä lukuun ottamatta vastakkaisia pareja.
Heksadekachoronin Schläfli-symboli on {3,3,4}. Sen kärkikuvio on säännöllinen oktaedri. Tetraederejä on 8, kolmioita 12 ja jokaisessa kärkipisteessä kohtaavia reunoja 6. Sen reunahahmo on neliö. Jokaisessa reunassa kohtaa 4 tetraedriä ja 4 kolmiota.
On olemassa 16-kennon alemman symmetrian muoto, jota kutsutaan demitesseraktiksi tai 4-demikuutioksi, joka kuuluu demihyperkuutio-perheeseen ja jota edustaa h{4,3,3}, ja se voidaan piirtää kaksivärisenä vuorotellen tetraedristen kennojen kanssa.
Kuvat
· 
Stereografinen projektio
· 
Neljä ortografista projektiota
· 
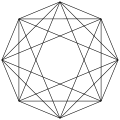
Viisto ortogonaaliprojektio sen säännöllisen kahdeksankulmaisen Petrie-polygonin sisällä, joka yhdistää kaikki kärjet paitsi vastakkaiset kärjet.
· 
16-solulla on kaksi Wythoffin rakennetta, säännöllinen muoto ja vuorotteleva muoto, jotka esitetään tässä verkkoina, joista jälkimmäistä edustavat vuorotellen kahden väriset tetraedriset solut.
· 
16-kennon 3D-projektio, jossa suoritetaan kaksinkertainen kierto kahden kohtisuoran tason ympäri.
Tessellations
4-ulotteinen euklidinen avaruus voidaan tesseloida säännöllisillä 16 solulla. Tätä kutsutaan heksadekaaniseksi hunajakennoksi, ja sen Schläfli-symboli on {3,3,4,3}. Kaksoistessellaatio, ikonitetrakoorinen hunajakenno, {3,4,3,3,3}, muodostuu säännöllisistä 24 solusta. Yhdessä tesseraktisen hunajakennon {4,3,3,4} kanssa nämä ovat ainoat kolme säännöllistä tessellointia R4 . Jokaisella 16-kennoisella on 16 naapuria, joiden kanssa se jakaa oktaedrin, 24 naapuria, joiden kanssa se jakaa vain yhden reunan, ja 72 naapuria, joiden kanssa se jakaa vain yhden pisteen. Tässä tessellaatiossa 24 16-kennoista kohtaa minkä tahansa pisteen.
Ennusteet
Solun 16 solun rinnakkaisprojektiolla 3-avaruuteen on kuutiomainen kuori. Lähimmät ja kauimmaiset solut projisoidaan kuution sisäänkirjoitetuiksi tetraedereiksi, mikä vastaa kahta mahdollista tapaa kirjoittaa säännöllinen tetraedri kuutioon. Kunkin tetraedrin ympärillä on neljä muuta (epäsäännöllistä) tetraedrimassaa, jotka ovat ympäröivien neljän tetraedrin solun kuvia ja täyttävät sisäänkirjoitetun tetraedrin ja kuution välisen tilan. Jäljelle jäävät 6 solua projisoidaan kuution neliöpinnoille. Tässä 16-kennon projektiossa kaikki sen reunat sijaitsevat kuution kuoren pinnoilla.
16-solun ensimmäisen solun perspektiiviprojektiolla 3-avaruuteen on triakis-tetraedrinen kuori. Solujen sijoittelu tämän kuoren sisällä on analoginen solu-suuntaisen rinnakkaisprojektion kanssa.
16-kennon kärkipiste-ensimmäinen rinnakkaisprojektio 3-avaruuteen on oktaedrinen. Tämä oktaedri voidaan jakaa 8 tetraedriseen tilavuuteen leikkaamalla koordinaattitasoja pitkin. Kukin näistä tilavuuksista on 16-solun soluparin kuva. Katsojaa lähinnä oleva 16-kennon huippu heijastuu oktaedrin keskipisteeseen.
Lopuksi reunan suuntaisella ensimmäisenä olevalla rinnakkaisprojektiolla on lyhennetty oktaedrinen kuori, ja kasvojen suuntaisella ensimmäisenä olevalla rinnakkaisprojektiolla on heksagonaalinen bipyramidikuori.
