Lineaarinen regressio — määritelmä, esimerkit ja sovellukset

Lineaarinen regressio on tapa tarkastella matematiikan avulla, miten jokin asia muuttuu, kun muut asiat muuttuvat. Lineaarisessa regressiossa käytetään riippuvaista muuttujaa ja yhtä tai useampaa selittävää muuttujaa suoran viivan luomiseksi. Tätä suoraa linjaa kutsutaan "regressiosuoraksi".

Lineaarinen regressio oli ensimmäinen monista regressioanalyysin suoritustavoista. Tämä johtuu siitä, että mallit, jotka riippuvat lineaarisesti niiden tuntemattomista parametreista, on helpompi sovittaa kuin mallit, jotka ovat epälineaarisesti yhteydessä parametreihinsa. Lineaarisen regression etuna on myös se, että tuloksena saatavien estimaattoreiden tilastolliset ominaisuudet on helpompi määrittää.

Lineaarisella regressiolla on monia käytännön käyttötarkoituksia. Useimmat sovellukset kuuluvat jompaankumpaan seuraavista kahdesta laajasta kategoriasta:

Lineaarista regressiota voidaan käyttää ennustavan mallin sovittamiseen havaittujen arvojen (tietojen) joukkoon. Tämä on hyödyllistä, jos tavoitteena on ennustaminen, ennustaminen tai vähentäminen. Jos tällaisen mallin kehittämisen jälkeen annetaan X:n lisäarvo ilman siihen liittyvää y:n arvoa, sovitettua mallia voidaan käyttää ennustetun y:n arvon muodostamiseen (kirjoitettuna y ^ {\displaystyle {\hat {y}}} ). ${\hat {y}}$
Kun muuttuja y ja joukko muuttujia X₁ , ..., X_p , jotka voivat olla yhteydessä y:hen, lineaarista regressioanalyysia voidaan soveltaa y:n ja X_j välisen suhteen voimakkuuden kvantifioimiseksi, sen arvioimiseksi, millä X_j ei ole lainkaan yhteyttä y:hen, ja sen tunnistamiseksi, mitkä X_j osajoukot sisältävät turhaa tietoa y:stä.

Lineaariset regressiomallit pyrkivät saamaan suoran ja datapisteiden välisen pystysuoran etäisyyden (eli jäännökset) mahdollisimman pieneksi. Tätä kutsutaan "suoran sovittamiseksi dataan". Usein lineaarisissa regressiomalleissa yritetään minimoida residuaalien neliöiden summa (pienimmät neliöt), mutta muitakin tapoja sovittamiseen on olemassa. Niitä ovat esimerkiksi "sopimattomuuden" minimointi jossakin muussa normissa (kuten pienimpien absoluuttisten poikkeamien regressiossa) tai pienimmän neliösumman häviöfunktion rangaistun version minimointi, kuten harjuregressiossa. Pienimmän neliösumman lähestymistapaa voidaan käyttää myös sellaisten mallien sovittamiseen, jotka eivät ole lineaarisia. Kuten edellä on esitetty, termit "pienimmät neliöt" ja "lineaarinen malli" liittyvät läheisesti toisiinsa, mutta ne eivät ole synonyymejä.

Perusmalli ja estimaatit

Yksinkertaisin lineaarisen regression malli on yhden selittävän muuttujan malli, joka voidaan kirjoittaa muodossa y = β0 + β1 x + ε, missä β0 on vakiotermi (intercept), β1 selittäjän vaikutus (kulmakerroin) ja ε satunnaisvirhe eli residuaali. Useamman selittävän muuttujan tapauksessa malli laajentuu muotoon y = β0 + β1 x1 + ... + βp xp + ε.

Usein käytetty estimaattori malliparametreille on pienimmän neliösumman (OLS, ordinary least squares) estimaatti, joka minimoi havaintojen ja mallin ennusteiden väliset neliölliset erot. OLS-estimaattorit saavat suljetun muodon matriisimuodossa: β̂ = (X'X)^{-1} X'y, kun X on selittävien muuttujien matriisi.

Tulkinta

Vakiotermi β0 kertoo ennustetun y-arvon, kun kaikki selittävät muuttujat ovat nollia (tulkinta riippuu muuttujien skaalasta ja merkityksestä).
Kulmakertoimet βj kertovat, miten odotettu y muuttuu, kun xj kasvaa yhdellä yksiköllä muiden muuttujien pysyessä vakioina.
R^2 mittaa selityskykyä: kuinka suuri osa y:n varianssista selittyy mallin avulla. Adjusted R^2 korjaa R^2:ta muuttujien lukumäärällä.

Oletukset ja diagnostiikka

Lineaarisen regression luotettavat johtopäätökset perustuvat usein seuraaviin perusoletuksiin:

Lineaarisuus: odotettu suhde selittäjien ja riippuvan muuttujan välillä on lineaarinen.
Itsenäisyys: havainnot ovat riippumattomia toisistaan (erityisesti aikaan tai paikkaan liittyvissä sarjoissa tätä pitää tutkia erikseen).
Homoskedastisuus: residuaalien varianssi on vakio eri selittävien muuttujien arvoilla.
Ei vakio- tai pienet poikkeamat normaalisuudesta: normaalisuus oletetaan usein pätevyyden testaamiseen ja luottamusväleihin, mutta suuret otoskoot vähentävät tämän merkitystä.

Diagnostiikkaan kuuluu residuaalikuvaajat (residuaalit vs. ennusteet), Q-Q -kuviot normaalisuuden tarkistamiseen, vaikutus- ja poikkeuspisteiden tunnistus (leverage, Cookin etäisyys) sekä multikollineaarisuuden arviointi (VIF-arvot).

Monimuuttujaisuus, kategorialliset muuttujat ja vuorovaikutukset

Lineaarinen malli laajenee helposti useaan selittävään muuttujaan. Kategorialliset muuttujat lisätään malliin yleensä dummy-muuttujina (esim. sukupuoli: 0/1). Lisäksi malleihin voidaan sisällyttää vuorovaikutustermiä (interaction), jos halutaan mallintaa tilanteita, joissa yhden selittäjän vaikutus riippuu toisen tasosta.

Regularisointi ja vaihtoehtoiset menetelmät

Kun muuttujia on paljon tai multikollineaarisuus/ylisovitus uhkaa, käytetään usein säännöstelymenetelmiä kuten ridge- tai lasso-regressiota, jotka lisäävät rangaistuksen parametreille estäen liian suuria kertoimia. Robustit menetelmät (esim. Huberin menetelmä tai pienimmät absoluuttiset poikkeamat) vähentävät herkkyyttä poikkeaville havainnoille.

Sovellusesimerkkejä

Taloustieteessä ennustetaan esimerkiksi kulutusta tai asuntojen hintoja (selittävät muuttujat: pinta-ala, sijainti, huoneiden määrä).
Biologiassa mallinnetaan esimerkiksi kasvien kasvua ravinnetason ja valon vaikutuksesta.
Tekniikassa lineaarista regressiota käytetään mittausvirheiden analysointiin ja kalibrointiin.

Rajoitukset ja varotoimet

Lineaarinen malli antaa luotettavia tuloksia vain, jos oletukset eivät riko analyysin perusperiaatteita vakavasti. Esimerkiksi voimakas epälineaarisuus tai korrelaatio havaintojen välillä voi johtaa harhaanjohtaviin tuloksiin.
Omiting variable -bias syntyy, jos merkittäviä selittäjiä jätetään pois.
Multikollineaarisuus tekee yksittäisten kertoimien tulkinnasta epävarmaa.

Mallin valinta ja validointi

Mallin valinnassa käytetään usein menetelmiä kuten askelvalintaa, AIC/BIC-arviointia tai ristiinvalidointia (cross-validation) ylisovituksen välttämiseksi. Ristiinvalidointi on erityisen hyödyllinen ennustetarkkuuden arvioinnissa.

Työkalut

Lineaarista regressiota voi toteuttaa monilla ohjelmistoilla ja kirjastolla: R (lm, glmnet), Python (statsmodels, scikit-learn), Stata, SPSS, Excel ja monet muut tarjoavat valmiit funktiot mallin sovittamiseen ja diagnostisiin testeihin.

Yhteenveto

Lineaarinen regressio on helppokäyttöinen, tulkittava ja usein ensimmäinen työkalu riippuvuussuhteiden analysointiin. Oikein käytettynä ja olettamuksia tarkastellen se antaa arvokasta tietoa sekä ennusteisiin että selittävien muuttujien vaikutusten ymmärtämiseen. On kuitenkin tärkeää huomioida mallin rajoitukset, tehdä diagnostiikkaa ja tarvittaessa käyttää vaihtoehtoisia tai rangaistuja menetelmiä.

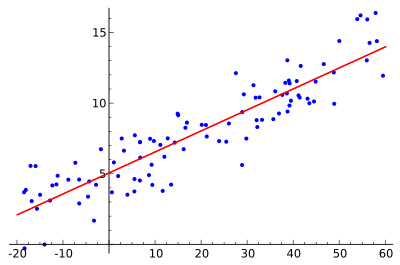
Ideana on löytää punainen käyrä, siniset pisteet ovat todellisia näytteitä. Lineaarisen regression avulla kaikki pisteet voidaan yhdistää yhdellä suoralla viivalla. Tässä esimerkissä käytetään yksinkertaista lineaarista regressiota, jossa punaisen viivan ja kunkin näytepisteen välisen etäisyyden neliö minimoidaan.

Käyttö

Taloustiede

Lineaarinen regressio on taloustieteen tärkein analyysiväline. Sitä käytetään esimerkiksi kulutusmenojen, kiinteiden investointimenojen, varastoinvestointien, maan viennin ostojen, tuontimenojen, likvidien varojen hallussapidon kysynnän, työvoiman kysynnän ja työvoiman tarjonnan arvaamiseen.

Aiheeseen liittyvät sivut

Käyrän sovitus
Logistinen regressio
Tavalliset pienimmät neliöt

Kysymyksiä ja vastauksia

K: Mitä on lineaarinen regressio?

V: Lineaarinen regressio on tapa tarkastella matematiikan avulla, miten jokin asia muuttuu, kun muut asiat muuttuvat. Siinä käytetään riippuvaista muuttujaa ja yhtä tai useampaa selittävää muuttujaa luomaan suora viiva, jota kutsutaan "regressiosuoraksi".

K: Mitkä ovat lineaarisen regression edut?

V: Mallit, jotka riippuvat lineaarisesti tuntemattomista parametreistaan, on helpompi sovittaa kuin mallit, jotka ovat epälineaarisesti yhteydessä parametreihinsa. Lisäksi tuloksena saatavien estimaattoreiden tilastolliset ominaisuudet on helpompi määrittää.

K: Mitä käytännön käyttötarkoituksia lineaarisella regressiolla on?

V: Lineaarista regressiota voidaan käyttää ennustavan mallin sovittamiseen havaittuihin arvoihin (tietoihin) ennusteiden, ennusteiden tai vähennysten tekemiseksi. Sitä voidaan käyttää myös muuttujien välisten suhteiden voimakkuuden kvantifiointiin ja sellaisten tietojen osajoukkojen tunnistamiseen, jotka sisältävät tarpeetonta tietoa toisesta muuttujasta.

Kysymys: Miten lineaarisilla regressiomalleilla pyritään minimoimaan virheet?

V: Lineaariset regressiomallit pyrkivät saamaan suoran ja datapisteiden välisen pystysuoran etäisyyden (residuaalit) mahdollisimman pieneksi. Tämä tehdään minimoimalla joko residuaalien neliösumma (pienimmät neliöt), sovittamattomuus jossakin muussa normissa (pienimmät absoluuttiset poikkeamat) tai minimoimalla pienimmän neliösumman häviöfunktion rangaistua versiota (harjuregressio).

Kysymys: Onko mahdollista, että lineaariset regressiomallit eivät perustu pienimpiin neliöihin?

V: Kyllä, on mahdollista, että lineaariset regressiomallit eivät perustu pienimpiin neliöihin, vaan käyttävät sen sijaan menetelmiä, kuten sovittamattomuuden minimointia jossakin muussa normissa (pienimmät absoluuttiset poikkeamat) tai pienimmän neliösumman häviöfunktion rangaistun version minimointia (harjuregressio).

Kysymys: Ovatko "lineaarinen malli" ja "pienimmät neliöt" synonyymejä?

V: Ei, ne eivät ole synonyymejä. Vaikka ne liittyvät läheisesti toisiinsa, "lineaarinen malli" viittaa nimenomaan suoran viivan käyttöön, kun taas "pienimmät neliöt" viittaa nimenomaan virheiden minimointiin varmistamalla, että viivan ja datapisteiden välillä on mahdollisimman vähän pystysuoraa etäisyyttä.