Newtonin liikkeen lait — Isaac Newtonin kolme klassisen mekaniikan peruslakia

Newtonin liikkeen lait: selkeä yhteenveto Isaac Newtonin kolmesta klassisen mekaniikan peruslaista, esimerkit ja sovellukset arjessa — lue lisää dynamiikan ymmärtämiseksi.

Tekijä: Leandro Alegsa

29-03-2026 23:54

Isaac Newton (1642-1727) tunnetaan laajalti dynamiikan eli liiketutkimuksen isänä. Hän kehitti kolme lakia, jotka ovat klassisen mekaniikan perusta. Niiden uskotaan pitävän paikkansa, koska tiedemiesten tekemien kokeiden tulokset ovat hänen lakiensa mukaisia.

Newtonin kolme liikettä koskevaa lakia

Ensimmäinen laki (inertialaki). Kappale pysyy levossa tai jatkaa liikettään vakionopeudella suoraviivaisesti, ellei siihen vaikuta jokin ulkoinen voima. Tämä määrittelee inertiaalisen koordinaatiston: paikoissa, joissa lakia noudatetaan suoraan, puhutaan inertiaalikehyksestä. Arkipäivän esimerkki: tyhjä raitiovaunu liukuu eteenpäin, kunnes jarrutusvoima pysäyttää sen.
Toinen laki (dynamiikan peruslaki). Kappaleen liikkeen muutos on verrannollinen kappaleeseen vaikuttavan nettovoiman suuruuteen ja tapahtuu voiman suuntaan. Matemaattisesti tämän voi kirjoittaa yksinkertaisena muodossa F = m a, missä F on nettovoima, m massa ja a kiihtyvyys. Yleisemmin voima on liikemäärän p aikaderivaatta: F = dp/dt (p = mv klassisessa tapauksessa). Tämä laki antaa tavan laskea kappaleen kiihtyvyys tunnetuista voimista.
Kolmas laki (voimien vuorovaikutus). Jokaisella voimalla on yhtä suuri ja vastakkainen vastavoima: jos kappale A vaikuttaa kappaleeseen B voimalla FAB, niin B vaikuttaa A:han voimalla FBA = −FAB. Huomaa, että nämä voimat vaikuttavat eri kappaleisiin, eivät samoihin. Tämä laki selittää mm. miksi potkaisemalla maata ihminen lähtee liikkeelle (toiminto: jalka kohdistaa voiman maahan; reaktio: maa kohdistaa voiman jalkaan).

Seuraukset ja sovelluksia

Liikemäärän ja impulssin säilyminen. Suljetussa systeemissä, jossa ulkoisia voimia ei ole, systeemin kokonaisliikemäärä säilyy. Tämä seuraa suoraan Newtonin lain muodoista ja kolmannesta laista.
Liikeongelmien laskeminen. Newtonin lait tarjoavat käytännöllisen menetelmän monien arkipäivän ja teknisten ongelmien ratkaisuun: ajoneuvon jarrutus, raketin työntövoima, pallon heitto, planeettojen liikkeet (kepleriläiset radat voidaan johtaa gravitaatiovoiman ja Newtonin lakien avulla).
Voimat ja kiihtyvyydet vektoreina. Newtonin lait ovat vektorilakeja: voimat, nopeudet ja kiihtyvyydet on otettava huomioon suunnat. Usein ongelmat vaativat voimat hajotettavaksi komponentteihin.

Rajoitukset ja laajennukset

Ei päde kaikkeen. Newtonin lait kuvaavat hyvin makroskooppista liikettä alhaisilla nopeuksilla (verrattuna valonnopeuteen) ja suurilla mittakaavoilla verrattuna atomien kokoon. Ne eivät kuitenkaan päde tarkasti relativistisissa tilanteissa (nopeudet lähellä c), joissa tarvitaan Einsteinin suhteellisuusteoriaa, eikä kvanttimekaniikan mittakaavassa, jossa kappaleiden käyttäytyminen on eri periaatteiden mukaista.
Ei-inertiaaliset kehykset. Jos analyysi tehdään kiihtyvässä (ei-inertiaalisessa) koordinaatistossa, Newtonin lait näyttävät rikkoutuvan, ellei mukaan lisätä ns. näennäisvoimia (esim. keskipakovoima, Coriolis-voima).
Määrä muuttuu raketeissa. Yksinkertainen muoto F = m a edellyttää, että massa m pysyy vakiona tai että käytetään liikemäärän muuttumisnopeutta F = dp/dt silloin kun massa muuttuu (kuten polttoainetta polttavassa raketissa).

Lyhyt historiallinen yhteys

Newton julkaisi suuret teoriansa teoksessaan Philosophiae Naturalis Principia Mathematica (1687). Newtonin lait yhdistivät kokeelliset havainnot ja matemaattisen kuvauksen siten, että niistä tuli klassisen mekaniikan kulmakivet. Monet myöhemmät kehitykset, kuten konservaatioperiaatteet ja differentiaaliyhtälöihin perustuvat laskumenetelmät, rakentuvat näiden lakien ympärille.

Käytännön huomioita

Kun ratkaiset liikettä koskevia tehtäviä, määritä ensin systeemi ja siinä vaikuttavat voimat, valitse sopiva koordinaatisto (inertiaali jos mahdollista) ja sovella F = ma tai dp/dt.
Muista huomioida kitka, ilmanvastus ja muut ei-ideaaliset voimat, jotka usein vaikuttavat arkipäivän esimerkeissä.

Newtonin kolme lakia antavat selkeän, käytännöllisen kehyksen monien fysikaalisten ilmiöiden ymmärtämiseen, vaikka niiden soveltamisala on rajallinen verrattuna myöhempiin teorioihin.

Kahden ensimmäisen lain alkuperäinen latinankielinen julkaisu.

Ensimmäinen laki

Jos kappale on levossa, se pysyy levossa, tai jos se on liikkeessä, se liikkuu tasaisella nopeudella, kunnes siihen kohdistuu nettovoima.

Tasainen nopeus tarkoittaa, että kappale liikkuu vakionopeudella muuttamatta suuntaa (eli suoraviivaisesti). "Nettovoima" tarkoittaa, että kappaleeseen vaikuttavat voimat eivät ole tasapainossa. Toisin sanoen ensimmäinen laki sanoo kaksi asiaa:

Paikallaan oleva esine liikkuu vain, jos siihen kohdistuu epätasapainoinen voima.
Liikkuva kappale muuttaa nopeuttaan tai suuntaansa vain, jos siihen kohdistuu epätasapainoinen voima.

Ensimmäisessä osassa todetaan, että maassa lepäävä pöytä ei liiku, ellei sitä työnnetä. Vaikka painovoima vaikuttaa pöytään ja vetää sitä alaspäin, maassa on reaktiovoima, joka työntää pöytää takaisin. Pöytään vaikuttavat voimat ovat tasapainossa, joten esine ei liiku.

Toista osaa on vaikeampi ymmärtää. Tasaisella pinnalla vierivä pallo hidastuu ja lopulta pysähtyy. Tämä johtuu kuitenkin kitkasta, joka on voima, joka hidastaa palloa. Myös rinteessä vierivään palloon vaikuttaa kitka, mutta painovoima, joka saa pallon liikkumaan, on voimakkaampi. Paikassa, jossa ei ole kitkan, ilmanvastuksen ja painovoiman voimia (esim. avaruudessa), liikkuva kappale jatkaisi liikkumistaan suoraviivaisesti, jos mikään voima ei hidastaisi sitä tai muuttaisi sen suuntaa.

Toinen laki

Hiukkaseen, jonka massa on $m,$ kohdistuva nettovoima $F$ on yhtä suuri kuin massa $m$ kertaa hiukkasen kiihtyvyys $a$ :

F = m a {\displaystyle \mathbf {F} =m\mathbf {a} } $\mathbf {F} =m\mathbf {a}$ .

Newtonin toisen lain mukaan hiukkasen kiihtyvyys riippuu hiukkaseen vaikuttavista voimista ja hiukkasen massasta. Jos hiukkasen nettovoima kasvaa, kiihtyvyys kasvaa. Mitä enemmän hiukkasella on massaa, sitä pienempi kiihtyvyys sillä on tietyllä nettovoimalla.

Esimerkiksi paino on voima, jonka tunnemme maapallolla ja joka johtuu painovoimasta. Hiukkasen paino $W$ saadaan seuraavasti

W = m g {\displaystyle \mathbf {W} =m\mathbf {g} } $\mathbf {W} =m\mathbf {g}$ ,

jossa $m$ on hiukkasen massa ja $g$ on paikallinen gravitaatiokiihtyvyys (jota ei pidä sekoittaa G:hen, universaaliin gravitaatiovakioon), joka vastaa noin 9,8 metriä sekunnissa² (32 jalkaa sekunnissa² ) maapallolla.

Voimme ilmaista Newtonin toisen lain momentin avulla. Hiukkasen impulssi $p määritellään$ sen massan $m$ ja nopeuden $v$ tulona:

p = m v {\displaystyle \mathbf {p} =m\mathbf {v} } $\mathbf {p} =m\mathbf {v}$ .

Hiukkasen kiihtyvyys $a$ on sen nopeuden $v$ aikaderivaatta:

a = d v d t {\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}} $\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}$ .

Siksi,

F = m a = m d v d t = d ( m v ) d t = d p d t {\displaystyle \mathbf {F} =m\mathbf {a} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}} $\mathbf {F} =m\mathbf {a} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$ .

Näin ollen meillä on toinen tapa esittää Newtonin toinen laki:

Hiukkaseen, jonka massa on $m,$ kohdistuva nettovoima $F$ on yhtä suuri kuin hiukkasen impulssin $p$ aikaderivaatta:

F = d p d t {\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}} $\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$ .

Klassisessa mekaniikassa toisen lain kaksi muotoa, F = m a {\displaystyle \mathbf {F} =m\mathbf {a} } $\mathbf {F} =m\mathbf {a}$ ja F = d p d t {\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}} $\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$ ovat täysin ekvivalentteja. Huomaa, että oletamme, että hiukkasen massa $m$ ei muutu.

Kolmas laki

Jokaiseen toimintaan liittyy yhtä suuri ja vastakkainen reaktio. Tai jokainen toiminta reagoi aina vastakkaiseen suuntaan.

Tämä on parhaiten ymmärrettävissä biljardipallojen avulla, joissa voimien toiminta/reaktioparit ovat helposti nähtävissä. Kun potkaiset jalkapalloa, pallo ei ainoastaan liiku, vaan tunnet myös voiman jalassasi.

Ensimmäiseen kappaleeseen kohdistuvien voimien suuruus on yhtä suuri kuin toiseen kappaleeseen kohdistuvan voiman suuruus. Ensimmäiseen kappaleeseen kohdistuvan voiman suunta on vastakkainen toiseen kappaleeseen kohdistuvan voiman suunnan kanssa. Voimat esiintyvät aina pareittain - yhtä suurina ja vastakkaisina toiminta-reaktiovoimapareina.

Luonnossa esiintyy erilaisia toiminta-reaktiovoimapareja. Tarkastellaan esimerkiksi kalan kuljettamista vedessä. Kala käyttää eviä työntääkseen vettä taaksepäin. Veteen kohdistuva työntö kuitenkin vain kiihdyttää vettä. Koska voimat syntyvät keskinäisestä vuorovaikutuksesta, veden on myös työnnettävä kalaa eteenpäin, jolloin kala kulkee veden läpi. Veteen kohdistuvan voiman suuruus on yhtä suuri kuin kalaan kohdistuvan voiman suuruus; veteen kohdistuvan voiman suunta (taaksepäin) on päinvastainen kuin kalaan kohdistuvan voiman suunta (eteenpäin). Jokaista toimintaa vastaa yhtä suuri (kooltaan) ja vastakkainen (suunnaltaan) reaktiovoima. Toiminta-reaktiovoimaparit mahdollistavat kalojen uinnin.

Ajattele auton liikettä matkalla kouluun. Autossa on pyörät, jotka pyörivät eteenpäin. Kun pyörät pyörivät eteenpäin, ne tarttuvat tiehen ja työntävät tietä taaksepäin. Koska voimat syntyvät keskinäisestä vuorovaikutuksesta, myös tien on työnnettävä pyöriä eteenpäin. Tiehen kohdistuvan voiman suuruus on yhtä suuri kuin pyöriin (tai autoon) kohdistuvan voiman suuruus; tiehen kohdistuvan voiman suunta (taaksepäin) on päinvastainen kuin pyöriin kohdistuvan voiman suunta (eteenpäin). Jokaiseen vaikutukseen liittyy yhtä suuri (suuruudeltaan) ja vastakkainen (suunnaltaan) reaktio. Vaikutus-reaktiovoimaparit mahdollistavat autojen liikkumisen tienpintaa pitkin.

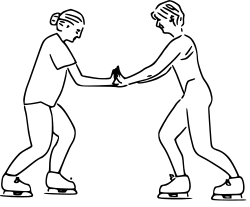
Newtonin kolmas laki. Luistelijoiden toisiinsa kohdistamat voimat ovat yhtä suuret ja vastakkaisiin suuntiin.

Aiheeseen liittyvät sivut

Philosophiæ Naturalis Principia Mathematica (Luonnonfilosofia)
Klassinen mekaniikka

Etsiä