Parallaksi — etäisyyksien mittaus tähtitieteessä ja stereopsis
Parallaksi — kuinka tähtitieteessä ja stereopsisissä mitataan etäisyyksiä: parsekit, Hipparcos, Gaia ja näön syvyystaju selitetty selkeästi.
Parallaksi tarkoittaa kohteen näennäistä sijainnin muuttumista, kun sitä havaitaan kahdesta eri paikasta; käytännössä kyse on kuvauskulmasta riippuvasta näennäissiirtymästä, eli siitä, miten kohteen suunta muuttuu havaitsijan siirtyessä. havaittu muutos voi johtua esimerkiksi Maan liikkeestä kiertoradallaan tai kahden silmän välisestä etäisyydestä.
Tähtitieteellinen parallaksi
Astronomiassa parallaksi on perustavanlaatuinen ja suorin tapa mitata etäisyyksiä aurinkokunnan ulkopuolisiin tähtiin. Yleisimmin käytetty on niin sanottu vuosittainen parallaksi: tähden sijan muutos maan kiertoliikkeen seurauksena, havaittuna kuuden kuukauden välein vastakkaisista kohdista Maan kiertorataa. Koska Maan kiertorata tunnetaan tarkasti, voidaan muodostaa geometrinen kolmio ja laskea etäisyys trigonometrian avulla.
Parallaksi mitataan kulmana, joka vastaa tähden näennäistä siirtymää taivasta vasten. Astronomiassa käytetty parallaksin yksikkö on usein kaarisekunti (arcsec) ja etäisyyden yksikkönä parsekki (pc). Parallaksin ja etäisyyden välinen perusyhtälö on yksinkertainen: d (pc) = 1 / p (arcsec), kun p on tähden vuosittainen parallaksi määriteltynä siten, että se vastaa kulmaa, jonka 1 astronominen yksikkö (AU) näyttää tähteen nähden. Käytännössä mitataan kulma, jonka tähden suunta poikkeaa eri vuodenaikoina nähdyistä suunnista, ja etäisyys lasketaan tästä kulmasta.
Parallaksilla voidaan mitata etäisyyksiä myös aurinkokunnassa: esimerkiksi Kuuhun ja lähiobjekteihin sovelletaan diurnalista (päivänsisäistä) parallaksia, kun taas lähin tähti (Proxima Centauri) on mitattavissa vuosittaisen parallaksin avulla. Tähtitieteilijät käyttävät tätä periaatetta sekä Kuuhun että Aurinkoon ja muihin kohteisiin pääsyn etäisyyksien määrittämiseksi; tähtien kohdalla parallaksikulma määritellään kahden tähteen suuntautuvan näköyhteyden välisenä kulmana.
Mittauksen käytännön toteutus ja haasteet
- Mittausten perusta on tarkka taivaankappaleiden asemien määrittäminen eri aikoina, yleensä eri vuodenajoilla.
- Etäisyyslaskennassa käytetään Maan kiertoradan tunnettua kokoa (1 AU) ja havaittua parallaksikulmaa.
- Rajoitteita aiheuttavat instrumenttien tarkkuus, ilmakehän häiriöt (maanpäällisissä havainnoissa), tähtien oma liike (proper motion) ja valon sironta.
Menetelmä toimii parhaiten lähietäisyyksillä. Kun kohde on niin kaukana, että Maan kiertorata muodostaa liian pienen baselin suhteessa etäisyyteen, saamamme parallaksikulma on niin pieni, että mittaustarkkuus kärsii. Tällainen käytännön raja on luokkaa satoja — kymmeniä tuhansia — valovuosia riippuen havaintolaitteiston tarkkuudesta; perinteisesti tavallinen maininta on noin 100 valovuoden luokkaa ennen kuin parallaksi muuttuu vaikeasti mitattavaksi maasta käsin. Tätä ongelmaa korjataan paremmilla instrumenteilla, avaruuslaitteilla ja ketjutetuilla menetelmillä muiden etäisyysmittausten kautta.
Virhelähteet ja korjaukset
Mittaustuloksiin vaikuttavat mm. instrumentin systeematiiviset virheet, spektroskooppinen binäärisyys (tähti voi olla kaksoistähti), interstellaarinen sumu ja tilastolliset vinoumat. Modernissa analyysissa tehdään korjauksia seuraaviin tekijöihin:
- Ilmakehän refraktio (maanpäällisissä havainnoissa)
- Optiset ja detektorivirheet
- Tähden oma liike (proper motion) erotetaan parallaksista pitkäaikaisseurannalla
Historia ja avaruusmissiot
Parallaksin etu on ollut niin suuri, että se muodostaa perustan koko kosmiselle etäisyystikkaille, jonka avulla etäisyyksiä voidaan arvioida edelleen kaukaisempiin kohteisiin käyttämällä standardikykyjä, kuten Cepheid-muuttuvia tähtiä ja tyypin Ia supernovia. Merkittäviä hankkeita ovat olleet maalla tehtävien havaintojen lisäksi avaruusmissiot, jotka voivat mitata parallaxia ilman ilmakehän häiriöitä: vuosina 1989–1993 operoinut Hipparcos-satelliitti teki tarkkoja mittauksia yli 100 000 lähitähdestä ja paransi etäisyysmittauksia merkittävästi. Nykyään Avaruusalus Gaian on tarkoitus kartoittaa ja mitata noin miljardia tähteä, mikä ulottaa suorien parallaximittojen aluetta kauas galaksissamme ja mahdollistaa yksityiskohtaisen kolmiodatan muodostamisen tähtien liikkeistä ja etäisyyksistä.
Stereopsis — biologinen parallaksi
Monilla eläimillä, myös ihmisellä, on kaksi toisistaan hieman poikkeavaa näkökenttää tuottavaa silmää, mikä mahdollistaa syvyys- ja etäisyysarvion muodostamisen. Tätä kaksisilmäistä syvyysnäköä kutsutaan stereopsisiksi. Koska silmät sijaitsevat eri kohdissa päätä, ne näkevät saman kohtauksen hieman eri näkökulmasta; näiden kahden kuvan erotusta — binokulaarista disparityä — aivot tulkitsevat etäisyydeksi.
Stereopsis perustuu kahteen periaatteeseen:
- Binokulaarinen disparity: pienet erot kohteen sijainnissa kahdessa retinan kuvassa käännetään etäisyydeksi.
- Konvergenssi ja vergenssi: silmien kääntymiskulma tarjoaa lisätietoa objektiin nähden.
Biologinen parallaksi antaa erittäin tarkan paikallistuntemuksen lähietäisyyksillä (millimetrien ja senttimetrien tarkkuudesta useisiin metreihin), ja ihmisellä stereoacuity eli pienin erotettava syvyusero voi olla alle yhden kaarisekunnin suuruusluokkaa ihanteellisissa olosuhteissa. Siksi stereopsis on tärkeä esimerkiksi tarkassa kädentyössä ja hahmontunnistuksessa.
Sovelluksia ja teknologia
Parallaksin ja stereopsisin periaatteita hyödynnetään laajasti:
- Astronomiassa: suorat etäisyysmittaukset ja kosmisen etäisyystikkauksen perusta.
- Teknisessä näössä: robotiikassa ja konenäössä stereokameroilla määritetään etäisyyksiä ja luodaan 3D-malleja.
- Viihdeteollisuudessa: 3D-elokuvat, virtuaalitodellisuus ja laitteet hyödyntävät erillisiä näkymiä silmille luodakseen syvyysvaikutelman.
Yhteenvetona: parallaksi on yksinkertainen, mutta voimakas geometrinen menetelmä etäisyyksien mittaamiseen sekä luonnossa (silmät) että tieteessä (tähtitiede). Sen rajoitukset kaukana olevien kohteiden kohdalla ovat ajaneet kehittämään tarkempia havaintolaitteita ja pitämään parallaksimittauksia keskeisenä lähtökohtana kosmisten etäisyyksien määrittelyssä.
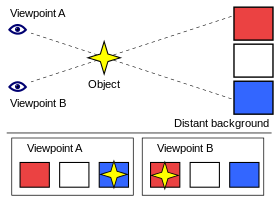
Esimerkki sijainnin muutoksesta johtuvasta kohteen parallaksista kaukana olevaa taustaa vasten. Kun kohdetta tarkastellaan näköalapaikalta A, se näyttää olevan sinisen neliön edessä. Kun katselupistettä muutetaan "katselupisteeseen B", kohde näyttää siirtyneen punaisen neliön eteen.
Kysymyksiä ja vastauksia
K: Mikä on parallaksi?
V: Parallaksi on kahdesta eri paikasta katsottuna havaittu kohteen sijainnin muutos. Se mitataan kahden havaintolinjan välisen kulman avulla, ja sitä voidaan käyttää etäisyyksien määrittämiseen.
K: Miten parallaksia käytetään tähtitieteessä?
V: Tähtitieteessä vuosittainen parallaksi on ainoa suora tapa mitata etäisyyttä aurinkokunnan ulkopuolisiin tähtiin. Tähtitieteilijät käyttävät parallaksin periaatetta mittaamaan etäisyyksiä taivaankappaleisiin, kuten Kuuhun, Aurinkoon ja aurinkokunnan ulkopuolisiin tähtiin.
K: Miten etäisyys lasketaan parallaksin avulla?
V: Tähtitieteelliset sijaintimittaukset tehdään eri vuodenaikoina. Koska Maan kiertorata tunnetaan tarkasti, voidaan laskea etäisyys sijainnista 1 sijaintiin 2. Horisontin ja kohteen välinen kulma voidaan mitata tarkasti, jolloin saadaan kolmio, jonka perusviiva ja kulmat tunnetaan tarkasti. Tästä kolmiosta voidaan trigonometrian avulla laskea parsekkeina ilmaistut etäisyydet.
Kysymys: Onko parallaksin käytössä kaukana olevien kohteiden mittaamisessa rajoituksia?
V: Kyllä, se ei onnistu sellaisten kohteiden kohdalla, jotka ovat niin kaukana, että Maan kiertorata on liian pieni riittävän suuren parallaksikulman muodostamiseksi tarkkoihin mittauksiin - noin 100 valovuoden päässä tai kauempana. On keksitty muitakin menetelmiä, mutta mikään niistä ei ole yhtä tarkka kuin parallaksi suhteellisen lähellä olevien kohteiden mittaamisessa.
Kysymys: Mitä satelliittia käytettiin vuosina 1989-1993 lähellä olevien tähtien mittaamiseen?
V: Hipparcos-satelliittia käytettiin tänä aikana yli 100 000 lähitähden mittaamiseen.
K: Mikä avaruusalus tekee samanlaisia mittauksia kuin Hipparcos teki? V: Gaia (avaruusalus) tekee samanlaisia mittauksia noin miljardista tähdestä.
Etsiä