Yhdensuuntaisuuspostulaatti (Eukleideen viides postulaatti) — määritelmä ja merkitys
Yhdensuuntaisuuspostulaatti (Eukleideen 5.) — selkeä määritelmä, historiallinen tausta ja merkitys euklidisessa sekä ei-euklidisessa geometriassa.
Geometriassa yhdensuuntaisuuspostulaatti on yksi euklidisen geometrian aksioomista. Sitä kutsutaan myös usein Eukleideen viidenneksi postulaatiksi, koska se on Eukleideen elementtien viides postulaatti.
Postulaatin keskeinen muotoilu kuuluu:
Jos leikkaat viivapätkän kahdella viivalla ja viivojen muodostamat kaksi sisäkulmaa ovat yhteensä alle 180°, nämä kaksi viivaa kohtaavat lopulta, jos jatkat niitä tarpeeksi pitkään.
Mitä postulaatti tarkoittaa käytännössä?
Yksinkertaisesti sanottuna yhdensuuntaisuuspostulaatti kertoo, miten suorat käyttäytyvät tasossa: se määrää, milloin kaksi suoraa joutuvat kohtaamaan ja milloin ne eivät kohtaa (eli ovat yhdensuuntaisia). Postulaatin avulla voidaan johtaa useita yleisiä euklidisen geometrian ominaisuuksia, kuten kolmion kulmien summan olevan 180° ja sen, että pisteen kautta, joka ei kuulu annettuun suoraan, kulkee täsmälleen yksi suoralle yhdensuuntainen suora (Playfair’n aksiooma, ks. alla).
Vastineet ja ekvivalentit muotoilut
- Playfair'n aksiooma: Pisteen kautta, joka ei kuulu annettuun suoraan, kulkee täsmälleen yksi suora, joka ei leikkaa kyseistä suoraa. Tämä muotoilu on loogisesti ekvivalentti Eukleideen viidennelle postulaatille ja sitä käytetään usein nykyaikaisissa aksioomajärjestelmissä.
- Monia muita lausemuotoja on esitetty, esimerkiksi lauseita kolmion kulmien summasta tai suorille etäisyyteen liittyviä väittämiä — kaikki nämä ovat euklidisen postulaatin kanssa yhtäpitäviä.
Merkitys ja seuraukset
Yhdensuuntaisuuspostulaatin hyväksyminen tai hylkääminen vaikuttaa geometrian perustavanlaatuisiin ominaisuuksiin. Joitakin suoria seurauksia postulaatista euklidisessa geometriassa:
- Kolmion sisäkulmien summa on 180°.
- Jos kaksi suoraa ovat kummankin kulman suhteen täsmälleen yhtä kallistuneet kolmannen suoran suhteen, ne ovat toistensa kanssa yhdensuuntaiset.
- Samankaltaisten kolmioiden ja yhdenmukaisten mittasuhteiden muodostuminen — monet geometriset konstruktiot ja mittasuhteet perustuvat tähän.
Historia ja riippumattomuus
Eukleides yritti Elementeissään todistaa viidennen postulaatin muista aksioomista, mutta yritykset epäonnistuivat. Vuosisatojen ajan matemaatikot epäilivät, olisiko postulaatti johdettavissa muista peruslauseista ja etsivät ristiriitoja. 1800-luvulla matemaatikot kuten Gauss, Nikolai Lobachevsky ja János Bolyai kehittivät itsenäisesti ei-euklidisia geometrioita, joissa viides postulaatti ei päde; näin osoitettiin, ettei postulaattia voi todistaa muista Eukleideen aksioomista ilman lisäoletuksia.
Myöhemmin Beltrami, Klein ja muut antoivat konkreettisia malleja (esim. Poincarén levy- ja puolitasamallit), jotka näyttivät ei-euklidisten geometrian järjestelmien olevan loogisesti yhdenmukaisia, jos euklidinen geometria on yhdenmukainen.
Ei-euklidiset vaihtoehdot
Kun viides postulaatti poistetaan tai korvataan jollain muulla väitteellä, syntyy ainakin kaksi selkeää vaihtoehtoa:
- Hyperbolinen geometria: Pisteen kautta, joka ei kuulu annettuun suoraan, kulkee yli yksi suora, joka ei leikkaa kyseistä suoraa (eli äärettömän monta "paralleelia"). Tässä geometriassa kolmion kulmien summa on alle 180°.
- Elliptinen (sferinen) geometria: Suorat (esim. pallon suurpiirit) leikkaavat aina, joten ei ole olemassa eriäviä "paralleeleja". Tässä kolmion kulmien summa on yli 180°.
Esimerkkinä elliptisestä tilanteesta toimii pallon pinta: suurpiirit (kuten maan päiväntasaaja ja pituuspiirit) kohtaavat aina, joten perinteistä yhdensuuntaisuutta ei ole.
Käyttö nykyajassa
Yhdensuuntaisuuspostulaatilla on yhä keskeinen rooli perusgeometriassa ja insinööritieteissä, mutta modernissa matematiikassa ja fysiikassa käytetään myös ei-euklidisia malleja. Esimerkiksi yleinen suhteellisuusteoria kuvaa avaruutta ja aikaa ei-euklidisella (kaarevalla) geometrialla, joten Eukleideen postulaatteja ei voida soveltaa suoraan avaruuden mittakaavassa.
Yhteenveto
Geometriassa yhdensuuntaisuuspostulaatti määrittelee, miten suorat kohtaavat tai pysyvät erillään tasossa. Se ei ole johdettavissa muista Eukleideen aksioomista, ja sen hyväksyminen tai korvaaminen johtaa erilaisiin geometrian lajeihin. Tästä syystä se on yksi matematiikan historiallisesti ja käsitteellisesti kiinnostavimmista aksioomista.
Geometriaa, joka noudattaa kaikkia Eukleideen aksioomia, kutsutaan euklidiseksi geometriaksi. Geometriaa, joka ei noudata kaikkia Eukleideen aksioomia, kutsutaan ei-euklidiseksi geometriaksi.
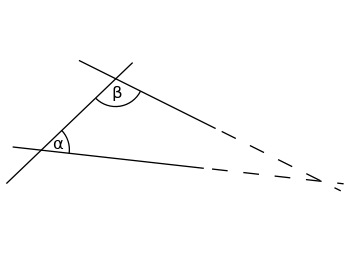
Jos sisäkulmien α (alfa) ja β (beeta) summa on pienempi kuin 180°, nämä kaksi suoraa leikkaavat toisensa jossain, jos molemmat on pidennetty äärettömään.
Historia
Joidenkin matemaatikkojen mielestä Eukleideen viides postulaatti oli paljon pidempi ja monimutkaisempi kuin neljä muuta postulaattia. Monet heistä ajattelivat, että se voitaisiin todistaa muiden yksinkertaisempien aksioomien perusteella. Jotkut matemaatikot ilmoittivat todistaneensa lauseen yksinkertaisemmista lauseista, mutta he kaikki osoittautuivat erehtyneiksi.
Playfairin aksiooma
Toinen uudempi lause, joka tunnetaan Playfairin aksiooman nimellä, muistuttaa Eukleideen viidettä postulaattia. Sen mukaan:
Jos on olemassa suora ja piste, joka ei ole tällä suoralla, voit piirtää tämän pisteen kautta vain yhden suoran, joka ei kohtaa toista suoraa.
Itse asiassa matemaatikot huomasivat, että tämä aksiooma ei ole vain samanlainen kuin Eukleideen viides postulaatti, vaan sillä on täsmälleen samat seuraukset. Matemaattisesti näitä kahta lausetta kutsutaan "ekvivalenttisiksi" lausekkeiksi. Nykyään matemaatikot käyttävät Playfairin aksioomaa useammin kuin Eukleideen alkuperäistä rinnakkaista postulaattia.
Epäeuklidinen geometria
Lopulta jotkut matemaatikot yrittivät rakentaa uusia geometrioita ilman aksioomaa. Erästä ei-euklidista geometriaa kutsutaan elliptiseksi geometriaksi. Elliptisessä geometriassa yhdensuuntaisuuspostulaatti on korvattu aksioomalla, jonka mukaan:
Jos on olemassa suora ja piste, joka ei ole tällä suoralla, et voi piirtää tämän pisteen kautta suoraa, joka ei lopulta risteäisi toisen suoran kanssa.
Matemaatikot huomasivat, että kun he korvasivat Eukleideen viidennen postulaatin tällä aksioomalla, he pystyivät silti todistamaan monet Eukleideen muista lauseista. Yksi tapa kuvitella elliptinen geometria on ajatella maapallon pintaa. Maapallolla pituuspiirien linjat näyttävät olevan yhdensuuntaisia päiväntasaajalla, mutta ne kohtaavat kaikki navoilla. 1800-luvun lopulla elliptinen geometria osoitettiin johdonmukaiseksi. Tämä osoitti, että Eukleideen viides postulaatti ei ollut riippumaton muista postulaateista. Tämän jälkeen matemaatikot lakkasivat enimmäkseen yrittämästä todistaa viidettä postulaattia muista neljästä postulaatista. Sen sijaan monet matemaatikot alkoivat tutkia muita geometrioita, jotka eivät noudata Eukleideen viidettä postulaattia.
Toinen aksiooma, jolla matemaatikot joskus korvaavat Eukleideen viidennen aksiooman, sanoo seuraavaa:
Kun on annettu suora ja piste, joka ei ole tällä suoralla, voit piirtää vähintään kaksi suoraa tämän pisteen kautta, jotka eivät lopulta risteä toisen suoran kanssa.
Tätä kutsutaan hyperboliseksi geometriaksi.
Toinen geometria yksinkertaisesti poistaa Eukleideen viidennen postulaatin eikä korvaa sitä millään. Tätä kutsutaan neutraaliksi geometriaksi tai absoluuttiseksi geometriaksi.
Etsiä