Lumivyöryvaikutus (kryptografia): mitä se on ja miksi se on tärkeä
Lumivyöryvaikutus kryptografiassa: miten pienet muutokset muuttavat salauksen ja hashien tuloksen täysin — keskeinen tekijä lohkosalausten ja tietoturvan vahvuudessa.
Lumivyöryilmiö ("maanvyöryilmiö) on lohkosalakirjoitusten ja kryptografisten hash-funktioiden algoritmien ominaisuus. Se tarkoittaa yksinkertaisesti sitä, että pieni muutos syötteessä aiheuttaa suuren ja näennäisesti satunnaisen muutoksen tulosteessa. Hyvissä lohkosalausalgoritmeissa ja hash-funktioissa tämä näkyy esimerkiksi niin, että yhden avaimen tai selkotekstin bitin kääntäminen muuttaa merkittävästi kaikkia salatekstin tai tiivisteen bittejä.
Miten lumivyöry toimii käytännössä
Lumivyöry ilmiö syntyy, kun algoritmi käyttää toistuvia vaiheita (rounds, iterointia) ja yhdistää syötteen bittejä monimutkaisilla operaatiolla kuten S-bokseilla, permutaatioilla ja XOR-operaatioilla. Tällöin pienet muutokset leviävät nopeasti läpi koko tilan, joten jokainen tulosteen bitti tulee riippuvaiseksi jokaisesta syötteen bitistä. Tämä parantaa algoritmin diffuusiota ja estää ennakoitavuutta.
Miksi lumivyöryvaikutus on tärkeä
Hyvä lumivyöryvaikutus tekee tuloksesta läpinäkymättömän: ilman lisätietoa ei voi tehdä luotettavia ennusteita syötteestä, vaikka tuotos olisi tiedossa. Jos lumivyöry puuttuu tai on heikko, salausanalyytikko voi hyödyntää riippuvuuksia ja tehdä ennusteita syötteestä, mikä voi johtaa osittaiseen tai täydelliseen murtamiseen. Tämä koskee sekä lohkosalausta että kryptografisia hash-funktioita, joissa pieni viestin muutos pitäisi aiheuttaa suuren muutoksen tiivisteessä (ns. "pienestä suureksi" -ominaisuus).
Teoreettisia mitoituksia ja vaatimuksia
Matemaattisesti lumivyöryä kuvataan usein perhosvaikutuksella. Kryptografiassa on myös käytössä tarkempia mittoja, kuten:
- Strict Avalanche Criterion (SAC): yhden sisääntulobitin muuttamisen pitäisi muuttaa kutakin lähtöbitin arvoa todennäköisyydellä 0,5.
- Bit Independence Criterion (BIC): eri lähtöbittien muutokset tulisi käyttäytyä toisistaan riippumattomasti, kun yksi sisääntulobitti käännetään.
Suunnitteluratkaisut ja käytännön rakenne
Siksi monet nykyaikaiset lohkosalakirjoitukset ovat niin kutsuttuja tuotesalakirjoituksia (product ciphers), joissa käytetään vuorotellen substituutioita (S-boksit) ja permutaatiota/sekoitusta. Useat kierrokset (rounds) ja suuret tietolohkot parantavat lumivyöryvaikutusta — sama periaate näkyy myös siinä, miksi hash-funktioilla on usein suuria lohkokokoja ja useita sekoitusvaiheita.
Lumivyöryn vaikutus kryptanalyysiin
Hyvä lumivyöry tekee vaikeammaksi hyödyntää erilaisia analyysimenetelmiä, kuten differentiaalista tai lineaarista kryptanalyysiä, koska hyökkääjän on paljon vaikeampi ennustaa miten pieni muutos syötteessä vaikuttaa tulokseen. Toisaalta heikko lumivyöry voi johtaa helposti löydettäviin riippuvuuksiin, jotka tuovat ennustettavuutta ja mahdollisuuden murtamiseen.
Yhteenveto ja käytännön huomioita
Se on yksi tärkeimmistä suunnittelutavoitteista, kun luodaan vahvaa salakirjoitusta tai kryptografista hash-funktiota. Suunnittelijat pyrkivät rakentamaan algoritmeihin hyvän lumivyöryvaikutuksen, koska se parantaa satunnaisuuden ja ennustamattomuuden tasoa. Termiä lumivyöryilmiö käytti ensimmäisenä Horst Feistel (Feistel 1973) ja myöhemmin käsite yhdistettiin osaksi Shannonin sekaannus- ja diffuusioperiaatteita (Shannonin sekaannusominaisuus).
Kun arvioit tai suunnittelet salausta, kiinnitä huomiota lumivyöryn lisäksi myös algoritmin muuhun kryptografiseen vahvuuteen: riittäviin kierrosmääriin, ei-lineaarisuuteen, avainsekoitukseen ja muihin tunnettuja hyökkäystapoja vastaan käytettyihin vastaanottamismenetelmiin. Näin varmistetaan, ettei satunnaistaminen ole vain näennäistä ja että salausanalyytikko ei voi tehdä ennusteita pelkän tuloksen perusteella.
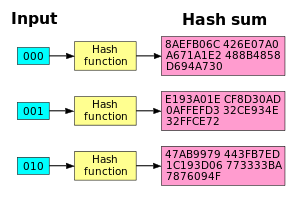
SHA1-hajausfunktiolla on hyvä lumivyöryvaikutus. Kun yksikin bitti muuttuu, hash-summasta tulee täysin erilainen.
Nimi
Nimen alkuperä on maanvyörymät. Pieni kivi voi pudota alas, mennä lumen mukana ja aiheuttaa tuhoisan maanvyöryn. Kivi oli pieni, mutta se saattoi aiheuttaa paljon tuhoa. Tämä on sama kuin mitä tämä vaikutus tekee. Pieni muutos syötteessä (kivi) muuttaa tulosta (maisemaa).
Tiukka lumivyörykriteeri
Strict Avalanche Criterion (SAC; "vahva maanvyörykriteeri") on boolen funktioiden ominaisuus. Sillä on merkitystä kryptografiassa. Se täyttyy, jos kaikki tulobitit muuttuvat 50 prosentin todennäköisyydellä, jos yhtä tulobittiä muutetaan.
SAC:n perustana olivat evoluution täydellisyyden ja lumivyöryn käsitteet. Webster ja Tavares esittivät sen vuonna 1985. Nykyään se on kaikkien nykyaikaisten salausjärjestelmien edellytys. Sen täyttivät esimerkiksi kaikki AES-kilpailun finalistit.
Bittiriippumattomuuskriteeri
Bittiriippumattomuuskriteeri (BIC; bitistä riippumaton kriteeri) on kriteeri. Se kuuluu seuraavasti: Kun yhtä tulobittiä muutetaan (käännetään), kahden lähtöbitin pitäisi muuttua toisistaan riippumatta. Tämä koskee kaikkia bittejä.
Se ei esimerkiksi olisi tyydyttävä, jos vain yksi lähtöbitti muuttuu, kun myös toinen lähtöbitti muuttuu. Ne saattavat muuttua vain siksi, että tulobitti muuttuu. Muuten lähtöbitit riippuisivat toisistaan.
Aiheeseen liittyvät sivut
- Sekaannus ja diffuusio
Kysymyksiä ja vastauksia
Q: Mikä on lumivyöryilmiö?
A: Lumivyöryilmiö (tunnetaan myös nimellä "maanvyöryilmiö") on lohkosalakirjoitusten ja kryptografisten hash-funktioalgoritmien ominaisuus, jonka mukaan pienen muutoksen avaimessa tai selkotekstissä pitäisi aiheuttaa voimakas muutos salatekstissä.
K: Kuka käytti ensimmäisenä termiä "lumivyöryilmiö"?
V: Horst Feistel käytti termiä lumivyöryilmiö ensimmäisen kerran vuonna 1973.
K: Miten se liittyy Shannonin sekaannusominaisuuteen?
V: Lumivyöryilmiön käsite tunnistettiin Shannonin sekaannusominaisuudesta, jonka mukaan jos lohkosalaus- tai salaushässifunktio ei täytä tätä astetta merkittävässä määrin, sen satunnaistaminen on heikkoa ja se voidaan murtaa (cracked) osittain tai kokonaan.
Kysymys: Mitä suunnittelutavoitteita on asetettu vahvoja salakirjoituksia luotaessa?
V: Kun luodaan vahvoja salakirjoituksia, niihin yritetään rakentaa hyvä lumivyöryilmiö matemaattisten periaatteiden, kuten perhosilmiön, avulla. Tämän vuoksi useimmat lohkosalakirjoitukset ovat tuotesalakirjoituksia ja siksi hash-funktioissa on suuria tietolohkoja.
K: Mitä tapahtuu, jos algoritmi ei täytä lumivyöryvaikutusta?
V: Jos algoritmi ei täytä lumivyöryilmiötä merkittävässä määrin, sen satunnaistaminen on heikkoa, ja kryptoanalyytikot, jotka pystyvät tekemään ennusteita syötteestä vain annettujen tulosteiden perusteella, voivat murtaa (murtaa) sen osittain tai kokonaan.
Kysymys: Miksi useimmat lohkosalakirjoitukset käyttävät tuotesalakirjoituksia?
V: Useimmat lohkosalakirjoittajat käyttävät tuotesalakirjoittajia, koska niiden avulla niihin voidaan rakentaa hyviä avalance-vaikutuksia matemaattisten periaatteiden, kuten perhosvaikutuksen, avulla.
K: Miksi hash-funktioilla on suuret tietolohkot?
V: Hash-funktioissa on suuria tietolohkoja, koska ne auttavat rakentamaan niihin hyviä avalance-vaikutuksia käyttämällä matemaattisia periaatteita, kuten perhosvaikutusta.
Etsiä