Algoritmi

Algoritmien vertailu

Ongelman ratkaisemiseen on yleensä useampi kuin yksi tapa. Voi olla monia erilaisia reseptejä tietyn ruokalajin valmistamiseksi, joka näyttää erilaiselta mutta maistuu lopulta samalta. Sama pätee algoritmeihin. Jotkin näistä tavoista ovat kuitenkin parempia kuin toiset. Jos resepti vaatii paljon monimutkaisia ainesosia, joita sinulla ei ole, se ei ole yhtä hyvä kuin yksinkertainen resepti. Kun tarkastelemme algoritmeja ongelmanratkaisutapana, haluamme usein tietää, kuinka kauan tietokoneelta kestäisi ratkaista ongelma tietyn algoritmin avulla. Kun kirjoitamme algoritmeja, haluamme algoritmimme vievän mahdollisimman vähän aikaa, jotta voimme ratkaista ongelmamme mahdollisimman nopeasti.

Ruoanlaitossa jotkin reseptit ovat vaikeampia toteuttaa kuin toiset, koska niiden valmistumiseen kuluu enemmän aikaa tai koska niissä on enemmän asioita, joita pitää seurata. Sama pätee algoritmeihin, ja algoritmit ovat parempia, kun ne ovat tietokoneen kannalta helpompia. Algoritmin vaikeutta mittaavaa asiaa kutsutaan monimutkaisuudeksi. Kun kysymme, kuinka monimutkainen algoritmi on, haluamme usein tietää, kuinka kauan tietokoneelta kestää ratkaista ongelma, jonka haluamme sen ratkaisevan.

Lajittelu

Tämä on esimerkki algoritmista, jolla lajitellaan värillisiä kortteja samanvärisiin kasoihin:

1. Poimi kaikki kortit.
2. Valitse kortti kädestäsi ja katso kortin väriä.
3. Jos kyseistä väriä olevia kortteja on jo kasassa, laita tämä kortti tähän kasaan.
4. Jos kyseistä väriä olevia kortteja ei ole kasassa, tee uusi kasa, jossa on vain tämän värisiä kortteja.
5. Jos kädessäsi on vielä kortti, palaa toiseen vaiheeseen.
6. Jos kädessäsi ei ole enää korttia, kortit lajitellaan. Olet valmis.

Lajittelu numeroiden mukaan

Nämä ovat esimerkkejä algoritmeista, joilla lajitellaan korttipino, jossa on useita eri numeroita, niin että numerot ovat järjestyksessä.

Pelaajat aloittavat korttipinoilla, joita ei ole lajiteltu.

Ensimmäinen algoritmi

Tämä algoritmi käy läpi korttipinon kortti kerrallaan. Korttia verrataan pinon seuraavaan korttiin. Huomaa, että tämä sijainti muuttuu vasta vaiheessa 6. Tätä algoritmia kutsutaan kuplalajitteluksi. Se on hidas.

1. Jos korttipino on tyhjä tai siinä on vain yksi kortti, se on lajiteltu; olet valmis.
2. Ota korttipino. Katso pinon ensimmäistä (ylintä) korttia.
3. Kortti, jota katsot, on kortti A. Kortti A on tällä hetkellä pinossa P.
4. Jos pinossa ei ole enää korttia A, siirry vaiheeseen 8.
5. Seuraava kortti pinossa on kortti B.
6. Jos kortin B numero on pienempi kuin kortin A, vaihda korttien A ja B sijainnit keskenään. Kun vaihdat kortteja, älä vaihda sijaintia P.
7. Jos pinossa on toinen kortti paikan P jälkeen, katso sitä; palaa vaiheeseen 3.
8. Jos et vaihtanut yhdenkään kortin paikkaa edellisessä kierroksessa, olet valmis; korttipino on lajiteltu.
9. Muussa tapauksessa palaa vaiheeseen 2.

Vaiheittainen esimerkki

Otetaan korttipino, jossa on numerot "5 1 4 2 8", ja lajitellaan se pienimmästä numerosta suurimpaan tämän algoritmin avulla. Algoritmi vertaa kussakin vaiheessa lihavoituja elementtejä. Korttipino on vasemmalla puolella.

Ensimmäinen läpikäynti:
( 5 1 4 2 8 ) → \displaystyle \to } ( 1 5 4 2 8 ) Tässä algoritmi vertaa kahta ensimmäistä elementtiä ja vaihtaa ne.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 4 2 5 8 ) Nämä elementit ovat jo järjestyksessä, joten algoritmi ei vaihda niitä.
Toinen läpikäynti:
( 1 4 2 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
Nyt korttipino on jo lajiteltu, mutta algoritmimme ei tiedä tätä. Algoritmi tarvitsee yhden kokonaisen läpikäynnin ilman vaihtoa, jotta se tietää, että pino on lajiteltu.
Kolmas läpikäynti:
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
Lopuksi joukko on lajiteltu, ja algoritmi voidaan lopettaa.

Historia

Tämä on helposti ymmärrettävä algoritmi lajitteluun. Tietojenkäsittelytieteilijät kutsuivat sitä nimellä Bubble sort, koska pienemmät elementit nousevat huipulle ja muuttavat asemaansa jokaisessa suorituksessa. Valitettavasti algoritmi ei ole kovin hyvä, koska lajitteluun kuluu paljon aikaa (korttipino käydään läpi monesti).

Toinen algoritmi

Tämä algoritmi käyttää toista ideaa. Joskus ongelman ratkaiseminen on vaikeaa, mutta ongelmaa voidaan muuttaa niin, että se koostuu yksinkertaisemmista ongelmista, jotka on helpompi ratkaista. Tätä kutsutaan rekursioksi. Sitä on vaikeampi ymmärtää kuin ensimmäistä esimerkkiä, mutta se antaa paremman algoritmin.

Perusajatus

1. Jos pinossa ei ole yhtään korttia tai siinä on vain yksi kortti, se on lajiteltu, ja olet valmis.
2. Jaa korttipino kahteen suunnilleen samankokoiseen puolikkaaseen. Jos kortteja on pariton määrä, toisessa pinossa on yksi kortti enemmän kuin toisessa.
3. Lajittele kumpikin pino tämän algoritmin avulla (aloita kummankin pinon osalta tämän luettelon kohdasta 1.).
4. Yhdistä nämä kaksi lajiteltua pinoa toisiinsa jäljempänä kuvatulla tavalla.
5. Tuloksena on lajiteltu korttipino. Olet valmis.

Kahden pinon yhdistäminen

Tämä toimii kahdella korttipinoilla. Toinen niistä on nimeltään A, toinen on nimeltään B. On olemassa kolmas pino, joka on alussa tyhjä, nimeltään C. Lopussa se sisältää tuloksen.

1. Jos joko pino A tai pino B on tyhjä, laita kaikki kortit siitä pinosta, joka ei ole tyhjä, pinon C päälle; olet valmis, pino C on yhdistämisen tulos. (Huomaa: ota koko pino ja laita se pinon C päälle; jos teet sen kortti kerrallaan, järjestys muuttuu, eikä se toimi niin kuin pitäisi).
2. Katso pinon A ja pinon B ylimpiä kortteja. Laita pinon C päälle se kortti, jonka numero on pienempi. Jos pinossa C ei ollut yhtään korttia, siinä on nyt yksi kortti.
3. Jos joko pinossa A tai pinossa B on jäljellä kortteja, palaa vaiheeseen 1 lajittelemaan ne.

Historia

John von Neumann kehitti tämän algoritmin vuonna 1945. Hän ei kutsunut sitä nimellä Lajittelu numeroiden mukaan, vaan nimellä Mergesort. Se on erittäin hyvä algoritmi lajitteluun verrattuna muihin.

Kolmas algoritmi

Ensimmäisellä algoritmilla korttien lajittelu kestää paljon kauemmin kuin toisella, mutta sitä voidaan parantaa. Kun tarkastellaan kuplalajittelua, voidaan huomata, että kortit, joilla on korkea numero, siirtyvät pinon yläreunasta melko nopeasti, mutta pinon alaosassa olevien korttien, joilla on matala numero, nousu (siirtyminen yläreunaan) kestää kauan. Ensimmäisen algoritmin parantaminen on seuraavanlainen ajatus:

Sen sijaan, että vertailtaisiin kahta vierekkäistä korttia, alussa valitaan erityinen kortti. Kaikkia muita kortteja verrataan sitten tähän korttiin.

1. Aloitamme pinosta A. On kaksi muuta pinoa B ja C, jotka luodaan myöhemmin.
2. Jos pinossa A ei ole kortteja tai siinä on vain yksi kortti, lajittelu on valmis.
3. Kortti valitaan pinosta A, jos mahdollista satunnaisesti. Tätä kutsutaan pivot-kortiksi.
4. Kaikkia pinon A jäljellä olevia kortteja verrataan tähän nivelkorttiin. Kortit, joiden luku on pienempi, menevät pinoon B, ja kortit, joiden luku on yhtä suuri tai suurempi, menevät pinoon C.
5. Jos pinoissa B tai C on kortteja, nämä pinot on lajiteltava samalla algoritmilla (aloitetaan listan pos. 1:stä sekä pinossa B että pinossa C vuorotellen).
6. Selvä. Lajitellussa korttipinossa on ensin lajiteltu pino B, sitten pivot ja sitten lajiteltu pino C.

Historia

Tämän algoritmin kehitti C. A. R. Hoare vuonna 1960. Se on nykyään yksi yleisimmin käytetyistä lajittelualgoritmeista. Sitä kutsutaan nimellä Quicksort.

Animaatio, joka näyttää, miten kuplalajittelu toimii


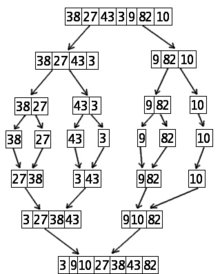
Lajittelu 7 numeroa käyttäen toista numeroiden lajittelualgoritmia (Mergesort).


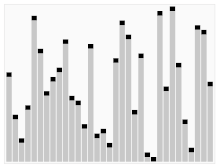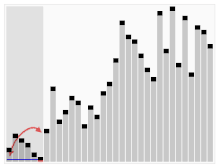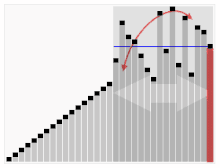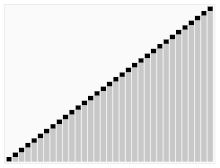
Kolmas algoritmi korttien lajitteluun. Punaisella viivalla oleva elementti valitaan niveleksi. Alussa se on elementti, joka on aivan oikealla. Tätä algoritmia kutsutaan Quicksortiksi.

Algoritmien kokoaminen yhteen

Jos pelaajilla on kortteja, joissa on värejä ja numeroita, he voivat lajitella ne värin ja numeron mukaan, jos he tekevät "lajittelu värien mukaan" -algoritmin, tekevät sitten "lajittelu numeroiden mukaan" -algoritmin kullekin värilliselle pinolle ja laittavat sitten pinot yhteen.

Lajittelualgoritmit numeroiden mukaan ovat vaikeampia kuin lajittelualgoritmi värien mukaan, koska vaiheet saatetaan joutua tekemään monta kertaa uudelleen. Voisi sanoa, että numeroiden mukaan lajittelu on monimutkaisempaa.

Aiheeseen liittyvät sivut

• Eukleideen algoritmi löydettiin yli 2000 vuotta sitten. Sen avulla voidaan löytää kahden luvun suurin yhteinen jakaja.