Jakolasku – määritelmä, symbolit ja esimerkit matematiikassa

Matematiikassa sana jakaminen tarkoittaa operaatiota, joka on kertolaskun käänteistoimenpide. Jakamisen yleisimmät merkit ovat vinoviiva ( / {\displaystyle /} $/$ ) ja murtoviiva, kuten seuraavassa:

6 / 3 {\displaystyle 6/3} $6/3$ tai 6 3 {\displaystyle {\frac {6}{3}}} ${\frac {6}{3}}$

Tässä esimerkissä lauseke tarkoittaa "6 jaettuna 3:lla", ja tulos on 2. Jakolaskussa ensimmäinen luku on jakoluku (tai osattava, tässä 6) ja toinen luku on jakaja (tässä 3). Jaon tulos on osamäärä, ja kokonaislukujen jaossa mahdollinen jäljelle jäävä osa kutsutaan jäännökseksi.

Esimerkiksi 14 / 4 {\displaystyle 14/4} $14/4$ antaa kokonaislukujen jaossa osamäärän 3 ja jäännöksen 2. Tämä voidaan ilmaista myös sekalukuna tai desimaalina: sekalukuna 3 1 2 {\displaystyle 3{\frac {1}{2}}}} $3{\frac {1}{2}}$ eli 3,5.

Jakamiseen liittyvät luvut voivat olla hyvin suuria. Esimerkiksi 200 / 5 = 40 {\displaystyle 200/5=40} $200/5=40$ tai suuremmissa lukuarvoissa: 7 , 000 , 000 , 000 / 1000 = 7 , 000 , 000 {\displaystyle 7,000,000,000,000/1000=7,000,000,000} $7,000,000,000/1000=7,000,000$ (tässä esimerkissä osamäärä on 7 miljoonaa tai 7 000 000).

Peruskäsitteet ja ominaisuudet

Jakaja ei voi olla nolla: jakaminen nollalla on määrittelemätöntä. Ilmaistaan usein lauseella "ei voi jakaa nollalla".
Ei vaihdettavuutta: jakaminen ei ole kommutatiivinen eli yleensä 6 ÷ 3 ≠ 3 ÷ 6.
Ei assosiatiivisuutta: jakaminen ei ole assosiatiivinen; esimerkiksi (8 ÷ 4) ÷ 2 ≠ 8 ÷ (4 ÷ 2).
Yhteys kertolaskuun: jakaminen on kertolaskun käänteinen operaatio: a ÷ b = c täsmää, kun b · c = a.

Jaon muotoja

Jakamisen tuloksen voi esittää usealla tavalla:

Kokonaislukujen jako antaa osamäärän ja mahdollisen jäännöksen (esim. 14 ÷ 4 = 3 jäännös 2).
Murtoluku kuvaa osamäärää tarkasti ilman jäännöstä: 14 ÷ 4 = 14/4, mikä sievennettynä on 7/2.
Sekaluku yhdistää kokonaisosan ja murto-osan: 3 1/2.
Desimaali voi olla päättyvä tai jaksollinen: 3,5 on päättyvä desimaali; 1/3 = 0,333… on toistuva desimaali.

Jakaminen eri lukutyypeillä

Jakaminen määritellään eri tavalla riippuen lukutyyppistä:

Kokonaisluvut: Euclidinen jakolause: jokaiselle kokonaisluvulle a ja positiiviselle jakajalle b on yksikäsitteiset osamäärä q ja jäännös r, joille pätee a = bq + r ja 0 ≤ r < b.
Rationaaliluvut: jakaminen vastaa murtoluvun muodostamista; a ÷ b = a · (1/b).
Reaaliluvut: jakaminen on määritelty, paitsi kun jakaja on nolla; tulos voi olla desimaali tai irrationaaliluku.
Negatiiviset luvut: merkkisääntö: tuloksen etumerkki määräytyy jakoluvun ja jakajan etumerkkien perusteella (eri merkit → negatiivinen, samat merkit → positiivinen).

Jakamisen menetelmät

Perinteisiä tapoja laskea jakolaskuja:

Pitkä jakaminen: vaiheittainen menetelmä suurten lukujen jakoon paperilla.
Murtolukusääntö: kahden murtoluvun jakaminen: (a/b) ÷ (c/d) = (a/b) · (d/c) = ad/bc (kun c ≠ 0).
Desimaalijako: jakaminen desimaaliluvuilla, jossa tarvittaessa lisätään nollia ja jatketaan jakoa halutun tarkkuuden saavuttamiseksi.

Jakolaskun käytännön esimerkkejä

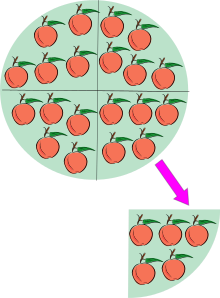
Jakaminen on arkipäivän käyttötilanteissa yleinen: jakaminen tasaerien löytämiseksi (esim. 12 omenaa 4 henkilölle → 3 omenaa/henkilö), pinta-alan laskuissa, yksikkömuunnoksissa ja talouslaskelmissa (esim. keskiarvon laskeminen).

Jakamisen testit ja jakavuussäännöt

Useimmat alatason jakolaskujen tarkistukset perustuvat jakavuussääntöihin, esim.:

Jaollisuus 2: luvun viimeinen numero on parillinen.
Jaollisuus 3: lukujen numeroiden summa on jaollinen kolmella.
Jaollisuus 5: luvun viimeinen numero on 0 tai 5.
Jaollisuus 9: numeroiden summa on jaollinen yhdeksällä.

Vältettävät virheet ja huomioitavaa

Älä jaa nollalla — operaatiota ei ole määritelty.
Kun yksiköt muuttuvat (esim. 1000 g = 1 kg), muista muuntaa ennen jakoa.
Huomioi pyöristyssäännöt desimaaleissa ja laskimen rajallisuus jaksollisia desimaaleja laskettaessa.

Yhteenveto

Jakolasku on keskeinen matematiikan perusoperaatio, jolla ilmaistaan luvun jakamista osiin. Se liittyy tiiviisti kertolaskuun ja murtolukuihin, ja sitä voidaan käsitellä eri tavoin riippuen lukutyyppistä (kokonaisluvut, rationaaliluvut, reaaliluvut). Peruskäsitteet — jakoluku, jakaja, osamäärä ja jäännös — auttavat ymmärtämään jaon tuloksen ja rakenteen.

20 / 4 = 5 {\displaystyle 20/4=5} $20/4=5$

Kertomalla

Jos c {\displaystyle c} $c$ kertaa b {\displaystyle b} $b$ on yhtä suuri kuin a {\displaystyle a} , kirjoitetaan seuraavasti:

c ⋅ b = a {\displaystyle c\cdot b=a} $c\cdot b=a$

Jos b {\displaystyle b} $b$ ei ole nolla, niin a {\displaystyle a} jaettuna b {\displaystyle b} $b$ on yhtä suuri kuin c {\displaystyle c} $c$ , kirjoitettuna seuraavasti:

a b = c {\displaystyle {\frac {a}{b}}=c}} ${\frac {a}{b}}=c$

Esimerkiksi,

6 3 = 2 {\displaystyle {\frac {6}{3}}=2} ${\frac {6}{3}}=2$

koska

2 ⋅ 3 = 6 {\displaystyle 2\cdot 3=6} $2\cdot 3=6$ .

Yllä olevassa lausekkeessa a {\displaystyle a} on nimeltään osinko, b {\displaystyle b} $b$ on jakaja ja c {\displaystyle c} $c$ on osamäärä.

Jakaminen nollalla, kuten

x 0 {\displaystyle {\frac {x}{0}}} ${\frac {x}{0}}$

ei ole määritelty.

Merkintä

Jakolasku esitetään useimmiten asettamalla jakolasku jakajan päälle siten, että niiden välissä on vaakasuora viiva, jota kutsutaan myös vinculumiksi. Esimerkiksi a {\displaystyle a} jaettuna b:llä {\displaystyle b} $b$ kirjoitetaan muodossa

a b {\displaystyle {\frac {a}{b}}} ${\frac {a}{b}}$

Tämä voidaan lukea "a jaettuna b:llä" tai "a yli b". Yksi tapa ilmaista jako yhdellä rivillä on kirjoittaa ensin jakolasku, sitten vinoviiva ja sitten jakaja, esimerkiksi näin:

a / b {\displaystyle a/b} $a/b$

Tämä on tavallinen tapa määritellä jako useimmissa tietokoneohjelmointikielissä, koska se voidaan helposti kirjoittaa yksinkertaisena merkkijonona.

Näiden kahden muodon puolivälissä oleva typografinen muunnos käyttää vinoviivaa, mutta korottaa osingon ja laskee jakajan:

^a⁄_b

Mitä tahansa näistä muodoista voidaan käyttää murtoluvun näyttämiseen. Murtoluku on jakolaskulauseke, jossa sekä jakaja että jakaja ovat kokonaislukuja (jolloin näitä kahta lukua kutsutaan yleensä osoittajaksi ja nimittäjäksi). Murtoluku on hyväksytty tapa kirjoittaa lukuja. Aina ei odoteta, että jakolaskun tulos kirjoitetaan desimaalilukuina.

Joissakin ei-englanninkielisissä kulttuureissa "a jaettuna b:llä" kirjoitetaan a : b {\displaystyle a:b} $a:b$ . Englanninkielisissä maissa kaksoispiste on kuitenkin rajoitettu ilmaisemaan siihen liittyvää suhdelukujen käsitettä (jolloin a : b {\displaystyle a:b} $a:b$ lukee "a on b:hen nähden").

Aiheeseen liittyvät sivut

Divisori, toinen merkitys on luku, joka jakaa määrän tasan.
Jakaminen kahdella
Pitkä jako
Modulaarinen aritmetiikka
Jäännös

Kysymyksiä ja vastauksia

K: Mitä sana "jako" tarkoittaa matematiikassa?

V: Jakaminen on matematiikassa operaatio, joka on kertolaskun vastakohta.

K: Mitkä ovat jakamisen symbolit?

V: Jakamisen symboleja ovat vinoviiva ( / ) ja murtoviiva.

K: Mikä on osinko jakotehtävässä?

V: Jako-ongelman ensimmäistä lukua kutsutaan osingoksi.

K: Mikä on jakajana jakotehtävässä?

V: Jakotehtävän toista lukua kutsutaan jakajaksi.

K: Mikä on jako-ongelman tulos?

V: Jako-ongelman tulosta kutsutaan osamääräksi, ja kokonaisluvuiksi jäävää määrää kutsutaan jäännökseksi.

K: Voiko jakamisessa käyttää isoja lukuja?

V: Kyllä, jakamisessa voidaan käyttää hyvin suuria lukuja, kuten kaksisataa tai seitsemän miljardia.