Kertolasku — määritelmä, ominaisuudet ja esimerkit

Kertolasku — selkeä määritelmä, tärkeimmät ominaisuudet ja havainnollistavat esimerkit. Opiskele kommutatiivisuus, kertojat ja käytännön sovellukset.

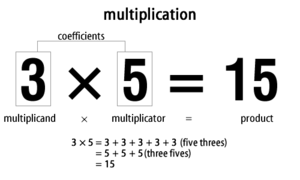
Kertolasku on aritmeettinen operaatio, jolla lasketaan kahden luvun tulo. Yksinkertaisin käsitys kertolaskusta on toistuva yhteenlasku: esimerkiksi "3 kerrottuna 5:llä" tarkoittaa kolmen lisäämistä viisi kertaa eli 3 + 3 + 3 + 3 + 3 = 15. Tämä voidaan merkitä muodossa 3 × 5 = 15 ja lausua "kolme kertaa viisi on viisitoista".

Visuaalinen tulkinta ja mittakaava

Luonnollisilla luvuilla kertolasku voidaan tulkita laattojen tai yksiköiden lukumääränä suorakulmiosta: jos toinen luku kertoo sarakkeiden määrän ja toinen rivien määrän, tuotteen avulla saadaan suorakulmion kokonaislaattojen määrä. Reaaliluvuilla kertolasku antaa vastaavanlaisesti suorakulmion pinta-alan, jossa sivujen pituudet ovat kerrottavat luvut.

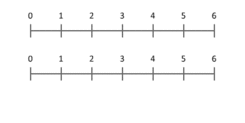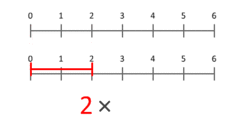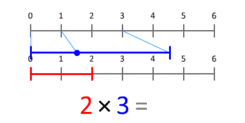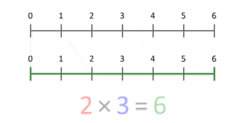
Kertolaskun voi myös ajatella skaalaavana toimena: jos toinen kerrottava on skaalauskerroin, kertominen siirtää tai venyttää arvoa. Tästä on hyötyä esimerkiksi kuvaamassa, kuinka pituus, pinta-ala tai määrä muuttuu, kun skalataan yhden ulottuvuuden arvoa. Animaatiossa, jossa 3 kerrotaan 2:lla, tuloksena on 6; sininen segmentti skaalautuu punaisen segmentin pituuden mukaan. Tämä selitys toimii myös, kun X on pienempi kuin 1 tai negatiivinen.

Perusominaisuudet

• Kommutatiivisuus: lukujen järjestys ei vaikuta tulokseen: a × b = b × a. Tämä pätee mm. kokonaisluvuille, rationaaliluvuille, reaaliluvuille ja kompleksiluvuille.
• Associatiivisuus: kertolasku on assosiatiivinen: (a × b) × c = a × (b × c). Tämä tarkoittaa, että usean luvun kertominen voidaan ryhmitellä millä tahansa tavalla.
• Distributiivisuus: kertolasku jakautuu yhteenlaskun yli: a × (b + c) = a × b + a × c.
• Neutraali alkio: luku 1 on kertolaskun neutraali alkio: a × 1 = a.
• Nolla: nollalla kertominen antaa aina nollan: a × 0 = 0. Nollalla ei kuitenkaan ole käänteislukua kertolaskussa (0:lla ei voi jakaa).
• Negatiivisten lukujen säännöt: miinus kertaa miinus antaa plus: (−a) × (−b) = a × b; miinus kertaa plus antaa miinuksen: (−a) × b = −(a × b).

Missä kertolaskun ominaisuudet eivät päde

Vaikka kertolasku on monilla lukujoukoilla kommutatiivista, tämä ei ole aina totta kaikissa rakenteissa. Esimerkiksi kvaternionit, tietyt vektorien operaatiot ja matriisit yleensä eivät ole kommutatiivisia: AB ei välttämättä ole sama kuin BA. Tällöin kertolaskun järjestyksellä on merkitystä.

Kertolaskun merkinnät ja käsitteitä

• Merkkejä ovat esimerkiksi ×, · tai pelkkä peräkkäisyys ilman merkkiä (esim. 3x tarkoittaa 3 × x).
• Kertojia voidaan kutsua tekijöiksi tai kertoimiksi. Jotkut matemaatikot puhuvat myös "kertolaskuosasta" ja "kertojasta".
• Kertomisen vastakohta on jakaminen: jakolasku on kertolaskun käänteistoimitus.

Kertolasku eri lukutyypeillä

• Kokonaisluvut ja luonnolliset luvut: kertominen vastaa toistuvaa yhteenlaskua ja soveltuu laskemiseen ilman murtolukuja.
• Murtoluvut ja rationaaliluvut: kertominen toimii murtoluvuilla siten, että (a/b) × (c/d) = (a×c)/(b×d).
• Desimaaliluvut ja reaaliluvut: kertominen skaalautuu jatkuvalle akselille, ja se vastaa usein geometrisia tai fysikaalisia suureita (pituus×leveys = pinta-ala).
• Kompleksiluvut: kertominen yhdistää amplitudia ja vaihetta (argumenttia) tason esityksessä.
• Kardinaaliluvut: kertomisen avulla voidaan tulkita joukko-opillisesti kahden joukon kartesiantuotteen kokoa; tästä kertoo mm. kardinaalilukujen kertolasku.

Esimerkkejä

• Perusesimerkki: 3 × 5 = 15 (kolme kertaa viisi = viisitoista).
• Negatiiviset: (−4) × 6 = −24 ja (−4) × (−6) = 24.
• Murtoluvut: 2/3 × 3/5 = 6/15 = 2/5.
• Desimaalit: 1,5 × 2 = 3,0.
• Area: suorakulmion sivujen pituudet 2 ja 3 antavat pinta-alan 2 × 3 = 6.

Käytännön huomioita ja laskutekniikat

• Pienet kertotaulut (esim. 1–10) opetellaan usein ulkoa helpottamaan laskemista.
• Suurempia lukuja kertotaessa käytetään pitkäkertomenetelmää tai laskinta; tietokoneissa ja ohjelmoinnissa kertolasku on perusoperaatio, jolla on optimointeja suurten lukujen ja liukulukujen käsittelyyn.
• Matriisikertolasku, skalaaritulo ja ristitulo ovat esimerkkejä tilanteista, joissa kertomista laajennetaan eri rakenteisiin ja joissa säännöt (esim. kommutatiivisuus) voivat muuttua.

Yhteenvetona: kertolasku yhdistää lukuja tuottaen niistä tuotteen. Se on keskeinen aritmetiikan operaattori, jolla on selkeä geometrinen, lukuteoreettinen ja operaatioiden välinen tulkinta. Kertolaskun tunteminen ja sen ominaisuuksien ymmärtäminen on tärkeää sekä peruslaskussa että korkeammassa matematiikassa.

Kysymyksiä ja vastauksia

Q: Mitä on kertolasku?

K: Millä nimellä kutsutaan kahta kerrottavaa lukua?

K: Onko kertolasku kommutatiivinen?

Kysymys: Miten voimme tulkita kardinaalilukujen kertolaskua?

Kysymys: Miten esitetään kolme kerrottuna viidellä?

K: Mikä on kertolaskun vastakohta?

Hae kirjaimella