Heaviside-funktio (yksikköaskel): määritelmä ja tärkeimmät ominaisuudet

Heaviside-funktio (yksikköaskel): selkeä määritelmä, epäjatkuvuus, yhteys Diracin deltaan ja keskeiset ominaisuudet säätö- ja signaaliteoriassa.

Tekijä: Leandro Alegsa

Heaviside-funktio H on epäjatkuva funktio, jonka arvo on nolla negatiiviselle syötteelle ja yksi positiiviselle syötteelle.

Funktiota käytetään säätöteorian matematiikassa kuvaamaan signaalia, joka kytkeytyy päälle tiettynä ajankohtana ja pysyy päällä määräämättömän ajan. Se on nimetty englantilaisen Oliver Heavisiden mukaan.

Heaviside-funktio on Diracin deltafunktion integraali: H′ = δ. Tämä kirjoitetaan toisinaan muotoon H′(t) = δ(t), kun tarkastelu tehdään distribuutioiden eli yleisten funktioiden (generalized functions) yhteydessä.

Määritelmä ja arvot

Yleinen yksikköaskelfunktion määritelmä on

H(t) = 0, kun t < 0; H(t) = 1, kun t > 0.

Arvo kohdassa t = 0 on epätarkka: käytännössä voidaan valita jokin arvo (yleisimmin 0, 1 tai 1/2). Monissa teoreettisissa yhteyksissä, erityisesti Fourier- ja Laplace-muunnosten yhteydessä, käytetään konventiota

H(0) = 1/2, koska se tekee monista kaavoista ja symmetrioista luontevampia.

Tärkeitä ominaisuuksia

  • Siirtymä: Siirretty funktio H(t − a) kuvaa kytkentää aikaan t = a.
  • Tuote ja leikkaus: H(t) kertaa jokin muu funktio f(t) vastaa funktion "kappaleen" valitsemista: f(t)H(t − a) esittää funktion käynnistymistä kohdasta a lähtien.
  • Suhde merkkiin: H(t) = (1 + sgn(t)) / 2 kaikilla t ≠ 0, missä sgn on signum-funktio.
  • Integraaliominaisuus: ∫_{−∞}^{t} δ(τ) dτ = H(t) (distributionaalisesti).
  • Derivaatta (distributionaalisesti): dH/dt = δ, eli Heaviside on deltafunktion integraali.

Muunnokset ja esitykset

  • Laplace-muunnos: Jos tarkastellaan aikafunktiota, joka on nolla negatiivisella puolivälillä, niin L{H(t)} = 1/s (Re(s) > 0).
  • Fourier-muunnos: Fourier-muunnos on distribuutio ja voidaan esittää muodossa F{H(t)} = πδ(ω) + PV(1 / (iω)), jossa PV tarkoittaa pääarvoa (Cauchy principal value).
  • Sileät approksimaatiot: Heaviside-funktio on raja-arvo monille sumeille askelille, esim. logistinen funktio 1 / (1 + e^{−k t}) tai virhefunktion (erf) avulla muodostettu muoto, kun k → ∞.

Sovelluksia

  • Säätö- ja signaalinkäsittely: Mallinnetaan kytkentöjä, pulssien alkamisia, järjestelmän vasteiden käynnistystä ja vaiheittaista ohjausta.
  • Differentiaaliyhtälöt: Käytetään paloittelemaan oikeanpuoleinen jäsen tai asettamaan ainestot eri aikaväleille; Heaviside-menetelmä auttaa erityisratkaisujen rakentamisessa.
  • Elektroniikka: Mallinnetaan kytkinten sulkeutumista/avautumista ja askelvastetta piireissä.
  • Teoreettinen analyysi: Distribuutioiden teoria ja spektrianalyysi hyödyntävät Heavisidea deltafunktion yhteydessä.

Esimerkkejä

1) Yksinkertainen aika-siirretty askel: u(t) = H(t − t0) on nolla ennen t0 ja yksi sen jälkeen.

2) Palapalatason funktio: jos halutaan funktio joka on f1(t) ennen t0 ja f2(t) jälkeen, voidaan kirjoittaa

f(t) = f1(t) (1 − H(t − t0)) + f2(t) H(t − t0).

Diskreetti vastine ja nimikkeistö

Diskreetissä ajassa käytetään usein termiä yksikköjono tai yksikköaskel u[n], jossa u[n] = 1 kun n ≥ 0 ja u[n] = 0 kun n < 0. Heaviside tunnetaan myös nimellä unit step function tai unit step.

Yhteenvetona: Heaviside-funktio on yksinkertainen mutta monikäyttöinen työkalu, joka ilmaisee kytkentöjen ja vaiheittaisten muutosten algebraisen mallin niin insinööri- kuin matematiikkasovelluksissa. Sen tiukat matemaattiset piirteet selviävät parhaiten distribuutioiden ja muunnosten (Laplace, Fourier) avulla.

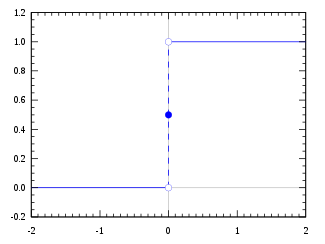
Heaviside-askel-funktio, jossa käytetään puolimaksimi-konventiota.  Zoom
Heaviside-askel-funktio, jossa käytetään puolimaksimi-konventiota.  

Diskreetti muoto

Voimme myös määritellä vaihtoehtoisen muodon Heavisiden askelfunktiolle diskreetin muuttujan n funktiona:

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\\1,&n\geq 0\end{cases}}} {\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}

jossa n on kokonaisluku.

Tai

H ( x ) = lim z → x - ( ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)} {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}

Diskreettiaikainen yksikköimpulssi on diskreettiaikaisen askeleen ensimmäinen erotus.

δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. } {\displaystyle \delta \left[n\right]=H[n]-H[n-1].}

Tämä funktio on Kroneckerin deltan kumulatiivinen summaus:

H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,} {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}

jossa

δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,} {\displaystyle \delta [k]=\delta _{k,0}\,}

on diskreetti yksikköimpulssitoiminto.

 

Edustukset

Usein on hyödyllistä käyttää Heavisiden askelfunktion integraaliesitystä:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e - i x τ d τ . {\displaystyle H(x)=\lim _{\epsilon \ to 0^{+}}-{1 \over 2\pi \mathrm {i} \int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} \int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } {\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .}  

H(0)

Funktion arvo kohdassa 0 voidaan määritellä seuraavasti: H(0) = 0, H(0) = ½ tai H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}}  

Aiheeseen liittyvät sivut

  • Laplace-muunnos
 

Kysymyksiä ja vastauksia

K: Mikä on Heaviside-funktio?


V: Heaviside-funktio on epäjatkuva funktio, jonka arvo on nolla negatiiviselle syötteelle ja yksi positiiviselle syötteelle.

K: Miksi Heaviside-funktiota käytetään ohjausteoriassa?


V: Heaviside-funktiota käytetään ohjausteoriassa kuvaamaan signaalia, joka kytkeytyy päälle tiettynä ajankohtana ja pysyy päällä loputtomiin.

K: Kenen henkilön mukaan Heaviside-funktio on nimetty?


V: Heaviside-funktio on nimetty englantilaisen Oliver Heavisiden mukaan.

K: Mikä on Heaviside-funktion ja Diracin deltafunktion välinen suhde?


V: Heaviside-funktio on Diracin deltafunktion integraali: H′(x)= δ(x).

K: Mitä Heaviside-funktio tuottaa positiivisille syötteille?


V: Heaviside-funktio antaa positiivisille syötteille tuloksen yksi.

K: Mitä Heaviside-funktio antaa negatiivisille syötteille?


V: Heaviside-funktio antaa nollan negatiivisille syötteille.

K: Minkä tyyppinen funktio on Heaviside-funktio?


V: Heaviside-funktio on epäjatkuva funktio.


Etsiä
AlegsaOnline.com - 2020 / 2025 - License CC3