Keskiarvo: määritelmä, laskeminen ja erot mediaaniin ja moodiin
Oppaasi keskiarvosta: määritelmä, laskeminen ja selkeät erot mediaaniin ja moodiin — opi, milloin käyttää mitäkin tilastollista keskilukua.
Keskiarvo on lukujoukon tyypillinen tai keskisuuri arvo, joka kuvaa lukujen keskitasoa. Aritmeettinen keskiarvo kertoo, kuinka suuri yksi havainto olisi, jos kaikkien havaintojen summa jaettaisiin tasan kaikkien havaintojen kesken.
Matematiikassa aritmeettista keskiarvoa kutsutaan usein pelkästään keskiarvoksi. Se saadaan laskemalla luvut yhteen ja jakamalla tulos lukujen lukumäärällä. On olemassa muitakin keskusarvoja ja mittoja, joita joskus kutsutaan "keskiarvoksi", kuten mediaani tai moodi (tilastotiede), jotka kuvaavat aineistoa eri tavoin.
Miten aritmeettinen keskiarvo lasketaan
Kun havaintoja on n kappaletta ja havainnot ovat x1, x2, …, xn, aritmeettinen keskiarvo lasketaan kaavalla:
keskiarvo = (x1 + x2 + ... + xn) / n
Esimerkki: lukujoukko {3, 7, 10} antaa keskiarvoksi (3 + 7 + 10) / 3 = 20 / 3 ≈ 6,67.
Painotettu keskiarvo
Jos eri havainnoilla on eri merkitys, käytetään painotettua keskiarvoa. Painotetussa keskiarvossa kukin havainto xi kerrotaan painolla wi, ja summa jaetaan painojen summalla:
painotettu keskiarvo = (w1·x1 + w2·x2 + ... + wn·xn) / (w1 + w2 + ... + wn)
Painotettua keskiarvoa käytetään esim. arvioissa, joissa tietyt mittaukset ovat luotettavampia tai toistuvat useammin.
Muita keskiarvoja
- Geometrinen keskiarvo sopii, kun tarkastellaan kasvukertoimia tai suhteellisia muutoksia (esim. sijoitusten tuotot). Se on n:nnessä juuren antajan lukujen tulosta: (x1·x2·...·xn)^(1/n).
- Harmoninen keskiarvo on käyttökelpoinen, kun lasketaan keskinopeuksia tai muita suhdelukuja: H = n / (1/x1 + 1/x2 + ... + 1/xn).
Erot mediaaniin ja moodiin
Mediaani on järjestetyn aineiston keskimmäinen arvo ja moodi on yleisin arvo. Keskiarvo, mediaani ja moodi kuvaavat aineistoa eri tavoin:
- Keskiarvo ottaa huomioon kaikkien havaintojen arvot, joten se on herkempi suurille tai pienille ääriluvuille (poikkeaville havainnoille).
- Mediaani ei ole herkkä ääriluvuille ja kuvastaa paremmin aineiston keskikohtaa, jos jakauma on vino.
- Moodi kertoo, mikä arvo esiintyy useimmin, mutta ei välttämättä kuvaa jakauman keskiosaa hyvin.
Esimerkiksi tulojen kohdalla muutama erittäin suuri arvo voi nostaa keskiarvoa paljon, kun taas mediaani pysyy lähellä tavallisten tulojen tasoa.
Kun käyttää keskiarvoa — hyödyt ja rajoitukset
- Keskiarvo on helppo laskea ja usein intuitiivinen tapa tiivistää aineistoa yhdellä luvulla.
- Herkkä poikkeaville havainnoille — jos aineisto sisältää äärilukuja, kannattaa harkita mediaania tai painotettua/rajattua keskiarvoa.
- Keskiarvo soveltuu hyvin esim. jatkuville ja symmetrisille jakaumille, mutta vähemmän hyvin vinoille jakautumille tai diskreeteille luokille ilman lisätulkintaa.
Otanta ja merkintä
Tilastotieteessä erotellaan usein populaation keskiarvo (merkitään usein μ) ja otoksen keskiarvo (merkitään x̄). Otoksen keskiarvo on estimaatti populaation keskiarvolle, ja siihen liittyy epätarkkuutta, joka voidaan kuvata esim. keskivirheellä tai luottamusväleillä.
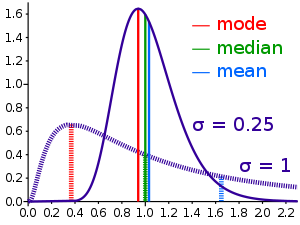
Kahden eri vinon jakauman aritmeettisen keskiarvon, mediaanin ja moodin vertailu.
Urheilu
Joissakin urheilulajeissa, kuten kriketissä ja baseballissa, keskiarvoja käytetään kertomaan, kuinka hyvä pelaaja on (esimerkiksi lyöntikeskiarvo). Urheilun keskiarvoilla on erityiset säännöt niiden löytämiseksi.
Kysymyksiä ja vastauksia
K: Mikä on keskiarvo?
V: Keskiarvo on lukujoukon "normaali" luku, joka on saatu aikaan sekoittamalla lukujoukko.
K: Miksi keskiarvoa kutsutaan matematiikassa?
V: Matematiikassa keskiarvoa kutsutaan keskiarvoksi.
K: Miten voimme löytää lukujen ryhmän keskiarvon?
V: Voimme löytää lukujen ryhmän keskiarvon laskemalla luvut yhteen ja jakamalla vastauksen lukujen lukumäärällä.
K: Onko olemassa muitakin keskiarvoja kuin keskiarvo?
V: Kyllä, on olemassa muitakin keskiarvoja kuin keskiarvo, kuten mediaani tai moodi (tilastotiede).
K: Mikä on mediaani tilastoissa?
V: Mediaani on tilastoissa aineiston keskimmäinen luku.
K: Mikä on moodi tilastoissa?
V: Tilastojen moodi on luku, joka esiintyy aineistossa useimmin.
K: Voiko lukujen ryhmällä olla useampi kuin yksi moodi?
V: Kyllä, numeroryhmällä voi olla useampi kuin yksi moodi, jos kaksi tai useampi luku esiintyy yhtä usein.
Etsiä