Todennäköisyysavaruus
Todennäköisyysavaruus on matemaattinen malli, jota käytetään tieteellisten kokeiden kuvaamiseen Todennäköisyysavaruus koostuu kolmesta osasta:
- Näyteavaruus, jossa luetellaan kaikki mahdolliset tulokset
- Joukko tapahtumia. Jokaiseen tapahtumaan liittyy nolla tai useampia tuloksia
- Funktio, joka määrittää todennäköisyydet kullekin tapahtumalle.
Tulos on mallin yhden suorituksen tulos. Koska yksittäisistä lopputuloksista voi olla vain vähän käytännön hyötyä, käytetään monimutkaisempia tapahtumia kuvaamaan lopputulosten ryhmiä. Kaikkien tällaisten tapahtumien kokoelma on σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}} 
. Lopuksi on tarpeen määritellä kunkin tapahtuman todennäköisyys. Tämä tehdään käyttämällä todennäköisyysmittafunktiota P.
Kun todennäköisyysavaruus on luotu, oletetaan, että "luonto" tekee siirtonsa ja valitsee yhden tuloksen ω otosavaruudesta Ω. Kaikkien F:n {\displaystyle \scriptstyle {\mathcal {F}}} tapahtumien, jotka sisältävät valitun lopputuloksen ω (muistutetaan, että jokainen tapahtuma on Ω:n osajoukko), sanotaan "tapahtuneen". Luonnon suorittama valinta tapahtuu siten, että jos koe toistettaisiin äärettömän monta kertaa, kunkin tapahtuman suhteelliset esiintymistiheydet vastaisivat funktion P määräämiä todennäköisyyksiä.
Merkittävä neuvostoliittolainen matemaatikko Andrei Kolmogorov esitteli todennäköisyysavaruuden käsitteen yhdessä muiden todennäköisyysaksioomien kanssa 1930-luvulla.
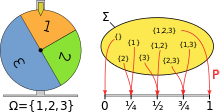
Onnenpyörän mallintaminen todennäköisyysavaruuden avulla
Kysymyksiä ja vastauksia
K: Mikä on todennäköisyysavaruus?
A: Todennäköisyysavaruus on matemaattinen malli, jota käytetään tieteellisten kokeiden kuvaamiseen. Se koostuu kolmesta osasta: näyteavaruudesta, jossa luetellaan kaikki mahdolliset lopputulokset, tapahtumien joukosta, johon liittyy nolla tai useampi lopputulos, ja funktiosta, joka määrittää todennäköisyydet kullekin tapahtumalle.
Kysymys: Mistä otosavaruus koostuu?
V: Otosavaruus koostuu kaikista mahdollisista lopputuloksista, jotka usein kirjoitetaan muotoon Ω. ja lopputulos muodossa ω {\displaystyle \omega }. .
K: Mikä on lopputulos?
V: Tulos on mallin yhden suorituksen tulos.
K: Mihin tapahtumia käytetään todennäköisyysavaruuksissa?
V: Tapahtumia käytetään luonnehtimaan tulosten ryhmiä, koska yksittäisistä tuloksista voi olla vain vähän käytännön hyötyä. Kaikkien tällaisten tapahtumien kokoelmaa kutsutaan σ-algebraksi, joka joskus kirjoitetaan F {\displaystyle {\mathcal {F}}} .
Kysymys: Miten todennäköisyydet osoitetaan kullekin tapahtumalle?
V: Kullekin tapahtumalle määritetään todennäköisyydet todennäköisyysmittafunktiolla P.
K: Kuka esitteli todennäköisyysavaruuden käsitteen? V: Merkittävä neuvostoliittolainen matemaatikko Andrei Kolmogorov esitteli todennäköisyysavaruuksien käsitteen yhdessä muiden todennäköisyysakselien kanssa 1930-luvulla.
