Joukko (matematiikka): määritelmä, perusominaisuudet ja esimerkit
Selkeä opas joukkoihin matematiikassa: määritelmä, jäsenyys, perusominaisuudet, yhtäsuuruus ja havainnolliset esimerkit nopeasti ymmärrettävästi
Joukko on matematiikan idea. Joukolla on jäseniä (joita kutsutaan myös alkioiksi). Joukko määritellään sen jäsenten avulla, joten kaksi joukkoa, joilla on samat jäsenet, ovat samoja (esim. jos joukolla 


Joukossa ei voi olla samaa jäsentä useammin kuin kerran. Ainoastaan jäsenyydellä on merkitystä. Jäsenillä ei ole esimerkiksi järjestystä tai muuta eroa. Mikä tahansa voi olla joukon jäsen, myös itse joukot (joskin jos joukko on itsensä jäsen, voi syntyä Russellin paradoksin kaltaisia paradokseja).
Määritelmä ja merkintä
Joukko ilmaistaan yleensä aaltosulkein merkitsemällä sen jäsenet: esimerkiksi {1, 2, 3} on joukko, jonka jäsenet ovat 1, 2 ja 3. Jos a on joukon A jäsen, kirjoitetaan a ∈ A; jos a ei kuulu joukkoon A, kirjoitetaan a ∉ A. Joukkojen yhtäsuuruus tarkoittaa, että ne sisältävät täsmälleen samat jäsenet: A = B silloin ja vain silloin, kun jokainen A:n jäsen on B:n jäsen ja päinvastoin.
Perusominaisuudet
- Uniikkius: saman jäsenen esiintyminen luettelossa merkitään vain kerran; setissä ei ole toistoa.
- Järjestyksen puute: {a, b} = {b, a}.
- Tyhjä joukko: joukko, jolla ei ole jäseniä, merkitään ∅ tai {}. Tyhjä joukko on kaikkien joukkojen osajoukko.
- Osajoukko: A on osajoukko B:tä (merkitään A ⊆ B), jos jokainen A:n alkio kuuluu myös B:hen. A on oikea osajoukko B:tä (A ⊂ B), jos A ⊆ B mutta A ≠ B.
- Kardinaliteetti: joukon alkioiden lukumäärää kutsutaan kardinaliteetiksi tai voimakkuudeksi ja merkitään usein |A|. Joukko voi olla loppuinen (esim. |A| = 4) tai ääretön (esim. luonnollisten lukujen joukko ℕ).
Peruslaskutoimitukset ja rakenteet
- Yhdiste: A ∪ B = {x | x ∈ A tai x ∈ B} — kaikki alkion, jotka kuuluvat jompaan kumpaan joukkoon.
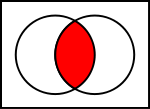
- Leikkaus: A ∩ B = {x | x ∈ A ja x ∈ B} — yhteiset alkiot.
- Erotus: A \ B = {x | x ∈ A ja x ∉ B} — A:n alkiot, jotka eivät kuulu B:hen.
- Komplementti: komplementti liittyy universaaliin joukkoon U: A^c = U \ A.
- Tehojoukko: P(A) tai 2^A on kaikkien A:n osajoukkojen joukko. Jos A on loppuinen ja |A| = n, niin |P(A)| = 2^n.
- Kartesiantuote: A × B = {(a, b) | a ∈ A, b ∈ B} — järjestettyjen pareja. Kartesiantuote laajenee monikkoihin A1 × A2 × ...
- Suhteet ja funktiot: relaatiot ovat osajoukkoja A × B; funktiot ovat erityisiä suhteita, joissa jokaiselle a ∈ A on liitetty täsmälleen yksi b ∈ B.
Merkintätapoja ja esitystavat
Joukkoja voidaan esittää usealla tavalla:
- Luettelemalla (roster): {a, b, c}.
- Ominaisuusmuodossa (set-builder): {x | ehto(x)}, esim. {x ∈ ℕ | x ≤ 5} = {1,2,3,4,5}.
- Symbolit ja erikoisjoukot: yleisiä symboleja ovat ℕ (luonnolliset luvut), ℤ (kokonaisluvut), ℚ (rationaaliluvut), ℝ (reaaliluvut) ja ℂ (kompleksiluvut).
Erityistapaukset ja huomautuksia
- Monijoukko (multisetti): perinteisestä joukosta poiketen monijoukossa sama alkio voi esiintyä useammin kuin kerran — tämä on eri käsite kuin tavallinen joukko.
- Järjestetty pari: (a, b) eroaa joukosta {a, b}, koska järjestys ja mahdollinen toistuminen merkitsevät.
- Joukkojen hierarkia: joukkojen joukko (esim. P(A)) on yleinen käsite: alkiot voivat olla myös itse joukkoja.
- Paradoksit: kuten mainittu, joukkojen käsittely ilman varovaisuutta voi johtaa paradokseihin (katso Russellin paradoksin artikkeli).
Esimerkkejä
- Yksinkertainen äärellinen: A = {a, e, i, o, u} — suomen kielen vokaalit.
- Tyhjä joukko: ∅ = {}.
- Luonnolliset luvut: ℕ = {0, 1, 2, 3, ...} (käytännössä eri määritelmissä voi alkaa 0:sta tai 1:stä).
- Tehojoukkoesimerkki: jos B = {1,2}, niin P(B) = {∅, {1}, {2}, {1,2}}.
- Kartesiantuoteesimerkki: {1,2} × {a,b} = {(1,a),(1,b),(2,a),(2,b)}.
Yhteenveto: joukko on peruskäsite matematiikassa, joka kuvaa kokoelmaa objekteja ilman järjestystä ja ilman toistoa. Joukko-opin peruskäsitteet — jäsenyys, osajoukko, yhdistelmät ja kartesiantuote — muodostavat pohjan monille matematiikan rakennelmille, kuten relaatioille, funktioille ja rakenteille teoriassa.
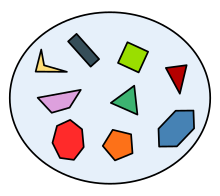
Esimerkki monikulmioiden joukosta

Georg Cantor vuonna 1894. Cantor oli ensimmäinen matemaatikko, joka puhui joukoista.

Cantorin alkuperäinen joukon määritelmä
Mitä tehdä joukkojen kanssa
Kuvittele, että setti on laukku.
Elementti
Laukkuun voidaan laittaa erilaisia asioita. Myöhemmin hyvä kysymys olisi, onko jokin tietty asia pussissa. Matemaatikot kutsuvat tätä elementtiä. Jokin on joukon alkio, jos kyseinen asia löytyy kyseisestä pussista. Tästä käytetty symboli on ∈ 

mikä tarkoittaa, että 



Toisin kuin pussi, joukko voi sisältää enintään yhden tietyn tyyppisen kohteen. Hedelmien joukossa ei siis ole merkitystä sillä, onko siinä yksi appelsiini vai 10 appelsiinia.
Tyhjä joukko
Kuten laukku, myös setti voi olla tyhjä. Tyhjä joukko on kuin tyhjä pussi: siinä ei ole mitään. Tyhjää joukkoa kutsutaan myös nollajoukoksi, ja sitä edustaa symboli
Maailmankaikkeus
Jos tarkastelemme esimerkiksi joitakin amerikkalaisten autojen joukkoja, esimerkiksi kaikkien Fordien ja kaikkien Dodgesien joukkoa, voimme myös haluta tarkastella koko amerikkalaisten autojen joukkoa. Tällöin kaikkien amerikkalaisten autojen joukkoa kutsutaan universumiksi.
Toisin sanoen universumi on kokoelma kaikkia niitä elementtejä, jotka halutaan ottaa huomioon tietyssä ongelmassa. Maailmankaikkeus on yleensä nimeltään 
Joukkojen vertailu
Kahta sarjaa voidaan verrata. Tämä on kuin katsoisi kahteen eri pussiin. Jos ne sisältävät samoja asioita, ne ovat samanarvoisia. Ei ole väliä, missä järjestyksessä nämä asiat ovat.
Jos esimerkiksi 

Joukon kardinaalisuus
Kun matemaatikot puhuvat joukosta, he haluavat joskus tietää, kuinka suuri joukko on (tai mikä on joukon kardinaalisuus). He tekevät tämän laskemalla, kuinka monta elementtiä joukossa on (kuinka monta esinettä pussissa on). Äärellisillä joukoilla kardinaalisuus on yksinkertainen luku. Tyhjän joukon kardinaalisuus on 0. Joukon 
Kahdella joukolla on sama kardinaalisuus, jos voimme yhdistää niiden elementit - jos voimme yhdistää kaksi elementtiä, yhden kummastakin joukosta. Joukko 



Ääretön kardinaalisuus
Toisinaan kardinaalisuus ei ole numero. Joskus joukon kardinaalisuus on ääretön. Kaikkien kokonaislukujen joukko on joukko, jolla on ääretön kardinaalisuus. Jotkin äärettömän kardinaalisuuden omaavat joukot ovat suurempia (niillä on suurempi kardinaalisuus) kuin toisilla. Esimerkiksi reaalilukuja on enemmän kuin luonnollisia lukuja, mikä tarkoittaa, että emme voi yhdistää kokonaislukujen joukkoa ja reaalilukujen joukkoa, vaikka tekisimme ikuisesti töitä.
Laskettavuus
Jos joukon elementit voidaan laskea, sitä kutsutaan laskettavaksi joukoksi. Laskettavia joukkoja ovat kaikki joukot, joilla on äärellinen määrä jäseniä. Laskettavissa oleviin joukkoihin kuuluvat myös jotkin äärettömät joukot, kuten luonnolliset luvut. Luonnolliset luvut voidaan laskea luvuilla 
Lukematon joukko on ääretön joukko, jota on mahdotonta laskea. Jos yritämme laskea alkioita, jätämme aina osan niistä laskematta. Sillä ei ole väliä, minkä askeleen otamme. Reaalilukujen joukko on laskematon joukko. On monia muitakin laskemattomia joukkoja, jopa niinkin pieni väli kuin ![{\displaystyle [0,1]}](https://www.alegsaonline.com/image/738f7d23bb2d9642bab520020873cccbef49768d.svg)
Osajoukot
Jos tarkastellaan joukkoa 

Sanomme: 
Kaavana se näyttää tältä:
Yleensä, kun kaikki joukon 



. Yleensä se luetaan " 

Esimerkki: Jokainen Chevrolet on amerikkalainen auto. Joten kaikkien Chevroletien joukko sisältyy kaikkien amerikkalaisten autojen joukkoon.
Aseta toiminnot
Sarjoja voidaan yhdistää eri tavoin.
Risteykset
Kahden joukon 



Esimerkki: Kun 


Liitot
Kahden joukon 





Esimerkki: Kun 


Täydentää
Täydennys voi tarkoittaa kahta eri asiaa:
komplementti on universumi
ilman kaikkia n
alkioita:
Universumi 
Esimerkki: Kun 

niin 
- Joukkojen
ja
erotus on joukko
ilman kaikkia joukon
alkioita:
Sitä kutsutaan myös 
Esimerkki: Kun 


Jos vaihdat joukot joukkoeroihin, tulos on erilainen: autojen esimerkissä ero 
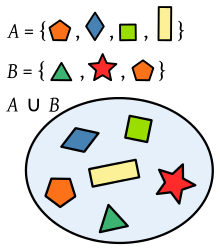
Kahden monikulmiojoukon unioni
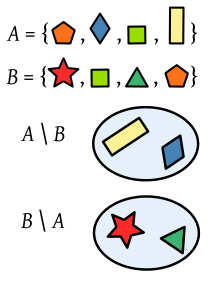
Kahden monikulmiojoukon erot
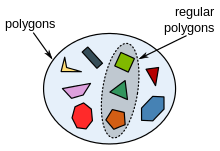
Säännöllisten monikulmioiden osajoukko
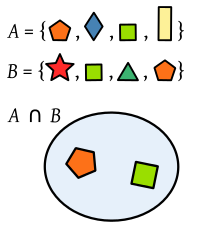
Kahden monikulmiojoukon leikkauspiste.
Merkintä
Useimmat matemaatikot käyttävät isoja ITALIALAISIA (yleensä roomalaisia) kirjaimia kirjoittaessaan joukoista (kuten 


Yksi tapa esittää joukko on luettelo sen jäsenistä, jotka on erotettu toisistaan pilkulla ja sisällytetty hakasulkeisiin. Esimerkiksi,
on joukko, jonka jäsenet ovat 1, 2 ja 3.
Toinen tapa, jota kutsutaan joukon rakentajan merkintätavaksi, on lausuma siitä, mikä on totta joukon jäsenistä, esimerkiksi näin:
- {x | x on luonnollinen luku & x < 4}.
Puhuttuna englanniksi tämä kuuluu näin: "kaikkien sellaisten x:ien joukko, joiden x on luonnollinen luku ja x on pienempi kuin neljä". Symboli [ipe "|" tarkoittaa "such that" tai "so that".
Tyhjä joukko kirjoitetaan erityisellä tavalla: 


Kun kohde a on joukon 
- a ∈ A.
Puhutulla englannilla tämä kuuluu näin: "a on n jäsen 
Venn-diagrammit
Matemaatikot käyttävät Venn-diagrammeja havainnollistamaan joukkoihin kohdistuvia operaatioita. Venn-diagrammeissa käytetään ympyröitä osoittamaan yksittäisiä joukkoja. Maailmankaikkeutta kuvataan suorakulmiolla. Operaatioiden tulokset esitetään värillisinä alueina. Leikkausoperaation havainnollistamisessa vasen ympyrä esittää joukkoa 

Erikoissarjat
Jotkin joukot ovat hyvin tärkeitä matematiikan kannalta. Niitä käytetään hyvin usein. Yksi näistä on tyhjä joukko. Monet näistä erikoisjoukoista kirjoitetaan taulun lihavoidulla kirjasinkirjoituksella, ja näitä ovat mm. seuraavat:
-
, joka tarkoittaa kaikkien alkulukujen joukkoa.
-
, joka tarkoittaa kaikkien luonnollisten lukujen joukkoa. Toisin sanoen,
= {1, 2, 3, ...}, tai joskus
= {0, 1, 2, 3, ...}.
-
, joka tarkoittaa kaikkien kokonaislukujen (positiivisten, negatiivisten tai nollan) joukkoa. Joten
= {..., -2, -1, 0, 1, 2, ...}.
-
, joka tarkoittaa kaikkien rationaalilukujen joukkoa (eli kaikkien oikeiden ja epäsuotuisten murtolukujen joukkoa). Siis
eli kaikki murtoluvut
, joissa a ja b kuuluvat kaikkien kokonaislukujen joukkoon ja b on eri kuin 0. Esimerkiksi
ja
. Kaikki kokonaisluvut kuuluvat tähän joukkoon, koska jokainen kokonaisluku a voidaan ilmaista murtolukuna
.
-
, joka tarkoittaa kaikkien reaalilukujen joukkoa. Tämä joukko sisältää kaikki rationaaliluvut sekä kaikki irrationaaliluvut (eli luvut, joita ei voi kirjoittaa murtoluvuiksi, kuten
ja √2).
-
, joka tarkoittaa kaikkien kompleksilukujen joukkoa.
Jokaisella näistä lukujoukoista on ääretön määrä alkioita, ja 
Joukkoja koskevat paradoksit
Matemaatikko Bertrand Russell havaitsi, että joukkojen epävirallisessa määrittelyssä on ongelmia. Hän totesi tämän paradoksissa, jota kutsutaan Russellin paradoksiksi. Helpommin ymmärrettävä versio, joka on lähempänä tosielämää, on nimeltään Barberin paradoksi.
Parturin paradoksi
Jossain on pieni kaupunki. Siinä kaupungissa on parturi. Kaikki kaupungin miehet eivät pidä parroista, joten he joko ajavat partansa itse tai menevät parturiin parturin ajettavaksi.
Voimme siis tehdä väitteen parturista itsestään: Parturi ajelee kaikki miehet, jotka eivät ajele itseään. Hän ajelee vain nämä miehet (koska muut ajelevat itse itsensä eivätkä tarvitse parturia ajamaan partaansa).
Tämä herättää tietenkin kysymyksen: Mitä parturi tekee joka aamu näyttääkseen puhtaaksi ajellulta? Tämä on paradoksi.
Jos parturi ajaa itse partansa, hän ei voi olla parturi, koska parturi ei aja itseään. Jos hän ei aja itseään, hän kuuluu niihin, jotka eivät aja itseään, eikä siis voi olla parturi.
Aiheeseen liittyvät sivut
- Cantorin joukko
- Ryhmäteoria
- Avoin sarja
- Suhde
- Joukkoteoria
Kysymyksiä ja vastauksia
Q: Mikä on sarja?
A: Joukko on matematiikan idea. Se koostuu jäsenistä (joita kutsutaan myös elementeiksi), jotka määritellään niiden jäsenten avulla, joten kaksi joukkoa, joilla on samat jäsenet, ovat samanlaisia.
K: Voiko joukossa olla sama jäsen useammin kuin kerran?
V: Ei, joukolla ei voi olla samaa jäsentä useammin kuin kerran.
K: Onko joukon järjestyksellä väliä?
V: Ei, järjestyksellä ei ole merkitystä joukossa. Mikä tahansa voi olla joukon jäsen, myös itse joukot.
K: Mitä tapahtuu, jos joukko on itsensä jäsen?
V: Jos joukko on itsensä jäsen, voi syntyä Russellin paradoksin kaltaisia paradokseja.
Kysymys: Onko joukoissa vain jäsenyydellä merkitystä?
V: Kyllä, jäsenyys on ainoa asia, jolla on merkitystä joukoille.
K: Mistä tiedät, ovatko kaksi joukkoa yhtä suuret?
V: Kaksi joukkoa on yhtä suuri, jos niillä on samat jäsenet.
Etsiä