Todennäköisyys – määritelmä, periaatteet ja laskuesimerkit
Tutustu todennäköisyyteen: selkeä määritelmä, keskeiset periaatteet ja vaiheittaiset laskuesimerkit kolikosta noppiin — opi laskemaan todennäköisyydet helposti.
Todennäköisyys on osa soveltavaa matematiikkaa. Se liittyy sattumaan ja niiden ilmiöiden tutkimiseen, jotka voivat tapahtua tai olla tapahtumatta.
Mitä todennäköisyys tarkoittaa?
Todennäköisyys on luku, joka kertoo, kuinka todennäköisesti jokin tapahtuma toteutuu. Todennäköisyyttä merkitään usein P(A), missä A on tapahtuma. Tapahtuman todennäköisyys (p) on aina nollan (mahdoton) ja yhden (varma) välillä. Todennäköisyys voidaan ilmaista murto-osana, desimaalina tai prosenttina.
Perusmäärittelyt ja aksioomat
- Otanta-avaruus (näytteen avaruus) Ω on kaikkien mahdollisten tulosten joukko.
- Tapahtuma A on Ω:n osajoukko.
- Todennäköisyysfunktio P täyttää seuraavat sääntöjä:
- 0 ≤ P(A) ≤ 1 kaikille tapahtumille A,
- P(Ω) = 1 (jokin tapahtuma Ω tapahtuu aina),
- Jos A ja B ovat keskenään toisensa poissulkevia (mutually exclusive), niin P(A ∪ B) = P(A) + P(B). Yleisemmin P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Komplementti, ehdollinen todennäköisyys ja riippumattomuus
- Komplementti: P(A^c) = 1 − P(A), missä A^c on tapahtuman A vastatapahtuma.
- Ehdollinen todennäköisyys: P(A | B) = P(A ∩ B) / P(B), kun P(B) > 0. Tämä kertoo todennäköisyyden A:lle oletuksella, että B tapahtui.
- Riippumattomuus: A ja B ovat riippumattomia, jos P(A ∩ B) = P(A) · P(B). Tällöin toisen tapahtuman tapahtuminen ei vaikuta toisen todennäköisyyteen.
Usein käytettyjä sääntöjä
- Multiplikaatiosääntö (itsenäisille tapahtumille): P(A ja B) = P(A) · P(B).
- Lisäämissääntö yleisesti: P(A tai B) = P(A) + P(B) − P(A ja B).
- Kun tarkastellaan useita itsenäisiä tapahtumia (esim. useita kolikkoheittoja tai nopanheittoja), todennäköisyys, että kaikki toteutuvat, on yksittäisten todennäköisyyksien tulo.
Esimerkkejä: kolikko ja noppa
Kolikko: Reilu kolikko antaa yleensä kaksi yhtä todennäköistä tulosta: kruuna ja klaava. Näin P(kruuna) = 1/2 = 0,5 = 50% ja P(klaava) = 1/2.
Noppa: Jos heitetään noppaa (monikko: noppa) ja oletetaan, että noppa on reilu, todennäköisyys sille, että sattuu juuri tietty luku, esimerkiksi 1, on 1/6. Sama pätee luvuille 2, 3, 4, 5 ja 6. Koska jokainen heitto tuottaa aina jonkin luvun 1–6, kaikkien mahdollisuuksien todennäköisyyksien summa on 1.
Useamman nopan heitot: kun heität kahta noppaa, mahdollisia järjestettyjä tuloksia on 6×6 = 36. Todennäköisyys saada täsmällinen järjestetty pari (esim. ensin 3 sitten 5) on 1/6 × 1/6 = 1/36 ≈ 0,0278. Jos halutaan esimerkiksi todennäköisyys saada molemmilla kuusi (6 ja 6), se on myös 1/36.
Summa kahdesta nopasta: summat vaihtelevat 2–12. Niiden todennäköisyydet eivät ole kaikki yhtä suuria, koska eri summia voi muodostaa eri määrällä yhdistelmiä. Esimerkiksi:
- P(summa = 2) = 1/36
- P(summa = 7) = 6/36 = 1/6
- P(summa > 10) = P(summa = 11 tai 12) = 2/36 + 1/36 = 3/36 = 1/12 ≈ 0,0833
Jos heität kolmea noppaa ja haluat tietyn järjestyksen, esimerkiksi 3, sitten 5 ja sitten 2, todennäköisyys on 1/6 × 1/6 × 1/6 = 1/216 ≈ 0,00463. Huomaa, että järjestyksen merkitys vaikuttaa lopputuloksen laskemiseen: jos kysytään "saaanko jossakin järjestyksessä 2, 3 ja 5" (eli kaikki kolme lukua, missä tahansa järjestyksessä), yhdistelmien lukumäärä on suurempi ja todennäköisyys kasvaa suhteessa yhtä järjestystä vastaavaan lukemaan.
Muita käsitteitä ja sovelluksia
- Odotusarvo (keskiarvo) E(X) kertoo satunnaismuuttujan pitkän aikavälin keskiarvon. Esimerkiksi yhden reilun nopan odotusarvo on (1+2+3+4+5+6)/6 = 3,5.
- Varianssi ja keskihajonta mittaavat, kuinka paljon tulokset tyypillisesti poikkeavat odotusarvosta.
- Todennäköisyyslaskentaa käytetään laajasti eri aloilla: tilastotieteissä, luonnontieteissä, koneoppimisessa, vakuutusalalla, riskienhallinnassa ja peleissä.
Lyhyt yhteenveto
Todennäköisyys antaa systemaattisen tavan arvioida satunnaisten tapahtumien esiintymisen todennäköisyyksiä. Perusperiaatteita ovat todennäköisyyden arvot väliltä 0–1, komplementtisääntö, lisä- ja multiplikaatiosäännöt sekä ehdollinen todennäköisyys. Yksinkertaisia esimerkkejä ymmärtämiseen tarjoavat kolikon ja nopan heitot; monimutkaisempiin tilanteisiin tarvitaan yhdistelmälaskentaa, permutaatioita ja joskus bayesilaista päättelyä. Todennäköisyyslaskenta on työkalu, jonka avulla satunnaisuutta voidaan mallintaa ja ennusteita tehdä järkevästi.
Todennäköisyyslaskentaa voidaan kehittää ja esittää myös matematiikan avulla; käytännössä se yhdistää loogisen päättelyn ja laskennan tarjoamaan täsmällisiä vastauksia satunnaisiin kysymyksiin.
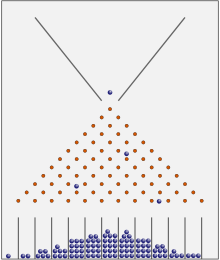
Papukoneessa tai Galton-laatikossa useimmat pallot päätyvät lähelle keskustaa. Pitkällä aikavälillä ne osoittavat normaalijakaumaa.
Todennäköisyyden ideat
Jacob Bernoullin, Pierre-Simon Laplacen ja Christiaan Huygensin kaltaiset ihmiset käyttivät sanaa todennäköisyys, kuten edellä on kuvattu. Muut ihmiset ajattelivat taajuuksia; heidän todennäköisyyskäsitteensä on yleensä nimeltään taajuustodennäköisyys.
Aiheeseen liittyvät sivut
- Luettelo matematiikan aiheista
- Todennäköisyysteoria
Kysymyksiä ja vastauksia
K: Mitä todennäköisyys on?
V: Todennäköisyys on sovelletun matematiikan osa, joka käsittelee sellaisten asioiden tutkimista, jotka voivat tapahtua tai olla tapahtumatta.
K: Miten todennäköisyys voidaan ilmaista?
V: Todennäköisyys voidaan ilmaista lukuna nollan (mahdoton) ja yhden (varma) välillä.
K: Mikä on esimerkki todennäköisyyden käytöstä?
V: Esimerkki todennäköisyyden käytöstä on sen osoittaminen, että heittämällä kolikon ilmaan ja antamalla sen laskeutua, puolet ajasta kolikko laskeutuu toinen puoli ylöspäin ja puolet ajasta toinen puoli ylöspäin.
K: Miten lasketaan todennäköisyys sille, että heitetään kahta noppaa ja saadaan tietty yhdistelmä?
V: Jos haluat laskea todennäköisyyden sille, että heitetään kahta noppaa ja saadaan tietty yhdistelmä, kerrotaan niiden kaksi todennäköisyyttä keskenään. Jos esimerkiksi haluaisit tietää, kuinka todennäköistä on saada ensin 3 ja sitten 5, se olisi 1/6 x 1/6 = 1/36.
Kysymys: Mitä tarkoittaa "klaava", kun puhutaan kolikoista?
V: Kolikoista puhuttaessa "klaava" tarkoittaa puolta, jossa ei ole kuvaa.
K: Kuinka todennäköistä on heittää kuutta noppaa ja saada luku, joka on suurempi kuin kymmenen? V: Todennäköisyys sille, että heitetään kuutta noppaa ja saadaan luku, joka on suurempi kuin kymmenen, voidaan laskea matematiikan ja tieteen avulla, mutta se ei ole itsestään selvää.
K: Mitä tapahtuu, kun kaksi todennäköisyyttä kerrotaan keskenään?
V: Kun kerrot kaksi todennäköisyyttä keskenään, lasket todennäköisyyden, että molemmat asiat tapahtuvat samanaikaisesti.
Etsiä