Ristitulo: määritelmä, laskeminen ja ominaisuudet vektoreissa

Ristitulo: selkeä määritelmä, laskuesimerkit, kaavat ja ominaisuudet 3D-vektoreissa. Opas auttaa ymmärtämään ristitulon ja laskemaan sen nopeasti.

Tekijä: Leandro Alegsa

27-02-2026 22:15

Ristitulo on matemaattinen operaatio, joka voidaan tehdä kahden vektorin välillä. Ristitulon seurauksena syntyy uusi vektori, joka on kohtisuorassa molempia tekijävektoreita vastaan. Klassinen ristitulo on luonnostaan määritelty kolmiulotteisessa euklidisessa avaruudessa (R^3), vaikka vastaavia rakenteita on mahdollista käsitellä myös muilla tavoilla korkeammissa ulottuvuuksissa.

Määritelmä ja laskeminen

Jos a = (a1, a2, a3) ja b = (b1, b2, b3) ovat vektoreita R^3:ssa, niiden ristitulo a × b lasketaan komponenttimuodossa:

a × b = (a2 b3 − a3 b2, a3 b1 − a1 b3, a1 b2 − a2 b1).

Usein ristitulo esitetään determinanttimuotoisena ilmaisuna yksikkövektoreiden i, j, k avulla:

a × b = det

i	j	k
a1	a2	a3
b1	b2	b3

Suunnaltaan ristitulo määrittyy oikean käden säännön mukaan: kun kolmella sormella osoitat a:n ja käännät kämmentäsi kohti b:tä, peukalo osoittaa a × b:n suuntaan.

Pituus ja geometrinen tulkinta

Ristitulon pituus on

|a × b| = |a| |b| sin θ,

missä θ on a:n ja b:n välinen kulma (0 ≤ θ ≤ π). Tämä pituus vastaa parallelogrammin pinta-alaa, jonka sivut ovat a ja b. Erityistapauksena, jos a ja b ovat samansuuntaiset (θ = 0 tai π), ristitulo on nollavektori.

Keskeiset ominaisuudet

Kohtisuoruus: a × b on kohtisuorassa sekä a:ta että b:tä vastaan (a · (a × b) = 0 ja b · (a × b) = 0).
Antikommutatiivisuus: a × b = −(b × a).
Distributiivisuus: a × (b + c) = a × b + a × c.
Skalaarikertolasku: (α a) × b = α (a × b) = a × (α b) kaikilla skalaarilla α.
Nollatapaus: a × a = 0 ja a × b = 0 silloin ja vain silloin, kun a ja b ovat lineaarisesti riippuvaiset (eli samansuuntaiset tai jompikumpi nollavektori).
Ei-assosiatiivisuus: Ristitulo ei yleensä ole assosiatiivinen: a × (b × c) ≠ (a × b) × c. Kuitenkin pätee vektoritriippelidentiteetti:
a × (b × c) = b (a · c) − c (a · b).
Skalaari kolmoistulo: a · (b × c) antaa parallelepipedin orientoidun tilavuuden ja on syklisesti invariantti: a · (b × c) = b · (c × a) = c · (a × b), mutta muuttuu merkkinsä, jos vaihtaa kahden tekijän järjestystä.

Esimerkki

Olkoot a = (1, 0, 0) ja b = (0, 1, 0). Silloin

a × b = (0 − 0, 0 − 0, 1 · 1 − 0 · 0) = (0, 0, 1),

mikä vastaa yksikkövektoria z-suunnassa ja |a × b| = 1 on pinta-ala yhdelle neliön neljännekselle tässä tapauksessa.

Laajennukset ja huomiot

Klassinen ristitulo on erityinen R^3:n rakenne. On kuitenkin olemassa vastaavia konstruktioita muissa ulottuvuuksissa: esimerkiksi tiettyjä vastaavuuksia on R^7:ssä liittyen Cayleyn oktonioneihin. Yleisemmin ulottuvuuden riippumattoman algebrallisen yleisrakenteen tarjoaa ulkoinen tulo (wedge- eli exterior-tulo), joka tuottaa bivektoreita (ei suoraan tavallisia vektoreita).
Kun käytät ristitulon laskukaavoja, huomioi yksiköt ja suunta; ristitulo voi esittää myös vektorikenttien vuorovaikutusta ja on tärkeä käsite fysiikassa (esim. momentti, magneettivoimat).

Ristitulon merkitys

Koska ristitulo on vektorioperaatio, se on erittäin tärkeä kaikenlaisissa tieteissä (erityisesti fysiikassa), tekniikassa ja matematiikassa. Yksi tärkeä esimerkki ristitulosta on vääntömomentti tai momentti. Toinen tärkeä sovellus liittyy magneettikenttään.

Ristitulon visualisointi kolmiulotteisesti

Ristitulo a → {\displaystyle {\vec {a}} ${\vec {a}}$ ja b → {\displaystyle {\vec {b}}} ${\vec {b}}$ on vektori, jota kutsumme c → {\displaystyle {\vec {c}}} : ${\vec {c}}$

c → = a → × b → {\displaystyle {\vec {c}}={\vec {a}}\times {\vec {b}}} ${\vec {c}}={\vec {a}}\times {\vec {b}}$

Tällöin c → {\displaystyle {\vec {c}}}} ${\vec {c}}$ suuruus on seuraava:

c = | c → | = | a → | | b → | sin θ = a b sin θ {\displaystyle c=|{\vec {c}}|=|{\vec {a}}|||{\vec {b}}|\sin \theta =ab\sin \theta } $c=|{\vec {c}}|=|{\vec {a}}||{\vec {b}}|\sin \theta =ab\sin \theta$ ,

jossa θ {\displaystyle \theta } $\theta$ on a → {\displaystyle {\vec {a}} ${\vec {a}}$ ja b → {\displaystyle {\vec {b}} ${\vec {b}}$ välinen kulma. Vektori a → × b → {\displaystyle {\vec {a}} \times {\vec {b}}} ${\vec {a}}\times {\vec {b}}$ on kohtisuorassa sekä a → {\displaystyle {\vec {a}} ${\vec {a}}$ että b → {\displaystyle {\vec {b}}} ${\vec {b}}$ kanssa. Suunta a → × b → {\displaystyle {\vec {a}} \times {\vec {b}}} ${\vec {a}}\times {\vec {b}}$ määräytyy oikean käden säännön muunnelman avulla. Jos pidät oikeaa kättäsi kuvan osoittamalla tavalla, peukalosi on suunnassa c → {\displaystyle {\vec {c}}} ${\vec {c}}$ , etusormi osoittaa suuntaan a → {\displaystyle {\vec {a}}} ${\vec {a}}$ ja toinen sormi osoittaa suuntaan b → {\displaystyle {\vec {b}}} ${\vec {b}}$ . Jos etusormen ja toisen sormen välinen kulma on suurempi kuin 180°, käsi on käännettävä ylösalaisin.

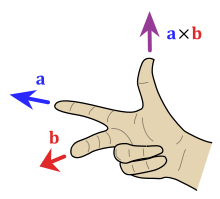
Ristitulon suunnan löytäminen.

Kuinka laskea ristitulo vektorimuodossa?

Kuten mikä tahansa matemaattinen operaatio, ristitulo voidaan tehdä suoraviivaisesti.

Kaksi ulottuvuutta

Jos
a → = ⟨ a 1 , a 2 ⟩ {\displaystyle {\vec {a}}=\langle a_{1},a_{2}\rangle } ${\vec {a}}=\langle a_{1},a_{2}\rangle$
ja
b → = ⟨ b 1 , b 2 ⟩ {\displaystyle {\vec {b}}=\langle b_{1},b_{2}\rangle } ${\vec {b}}=\langle b_{1},b_{2}\rangle$
niin sitten
a → × b → = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {\vec {a}}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}}} ${\vec {a}}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

tai

a → × b → = c → {\displaystyle {\vec {a}}\times {\vec {b}}={\vec {c}}} ${\vec {a}}\times {\vec {b}}={\vec {c}}$
ja
c → = ⟨ 0 , 0 , a 1 b 2 - a 2 b 1 ⟩ = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {\vec {c}}=\langle 0,0,a_{1}b_{2}-a_{2}b_{1}\rangle =(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}} ${\vec {c}}=\langle 0,0,a_{1}b_{2}-a_{2}b_{1}\rangle =(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

k ^ {\displaystyle {\hat {k}}} ${\hat {k}}$ on vain symboli, joka kertoo, että uusi vektorimme osoittaa ylöspäin (z-suunnassa). Jos "risteytät" kaksi vektoria, jotka molemmat ovat x-y-tasossa, tulo on aina kohtisuorassa molempiin vektoreihin nähden, ja jos molemmat vektorit ovat x-y-tasossa, ainoa tapa, jolla se voi olla kohtisuorassa molempiin, on olla z-suuntainen. Jos a 1 b 2 - a 2 b 1 {\displaystyle a_{1}b_{2}-a_{2}b_{1}}} $a_{1}b_{2}-a_{2}b_{1}$ arvo on positiivinen, se osoittaa sivun ulkopuolelle; jos sen arvo on negatiivinen, se osoittaa sivun sisälle.

Kolme ulottuvuutta

Jos
a → = ⟨ a 1 , a 2 , a 3 ⟩ {\displaystyle {\vec {a}}=\langle a_{1},a_{2},a_{3}\rangle } ${\vec {a}}=\langle a_{1},a_{2},a_{3}\rangle$
ja
b → = ⟨ b 1 , b 2 , b 3 ⟩ {\displaystyle {\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle } ${\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle$
silloin
a → × b → = ⟨ a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1 ⟩ {\displaystyle {\vec {a}}\times {\vec {b}}=\langle a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}\rangle } ${\vec {a}}\times {\vec {b}}=\langle a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}\rangle$

Ristitulon perusominaisuudet

a → × b → = - b → × a → {\displaystyle {\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}} ${\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}$

a → × ( b → + c → ) = a → × b → + a → × c → {\displaystyle {\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}} ${\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}$

c ( a → × b → ) = ( c a → ) × b → = a → × ( c b → ) {\displaystyle c({\vec {a}}\times {\vec {b}})=(c{\vec {a}})\times {\vec {b}}={\vec {a}}\times (c{\vec {b}})} } $c({\vec {a}}\times {\vec {b}})=(c{\vec {a}})\times {\vec {b}}={\vec {a}}\times (c{\vec {b}})$

Kysymyksiä ja vastauksia

K: Mikä on ristitulo?

A: Ristituote on matemaattinen operaatio, joka voidaan tehdä kahden kolmiulotteisen vektorin välillä.

K: Miten ristitulo usein esitetään?

V: Ristitulo esitetään usein symbolilla × tai \times.

K: Mitä tapahtuu ristitulon suorittamisen jälkeen?

V: Ristitulon suorittamisen jälkeen muodostuu uusi vektori.

K: Mikä on ristitulovektorin ja "ristiintaulukoitujen" vektoreiden välinen suhde?

V: Kahden vektorin ristitulo on aina kohtisuorassa (se muodostaa kulmanmuotoisen kulman) molempia "ristiintaulukoituja" vektoreita vastaan.

K: Missä ulottuvuudessa ristitulo yleensä toimii?

V: Ristitulo toimii yleensä vain kolmiulotteisessa avaruudessa.

K: Mitkä ovat ne kolme ulottuvuutta, joissa ristitulo voidaan suorittaa?

V: Ristiintaulukointi voidaan suorittaa kolmessa ulottuvuudessa: ylös tai alas, vasemmalle tai oikealle ja eteen tai taakse.

K: Miksi ristitulo toimii yleensä vain kolmiulotteisessa avaruudessa?

V: Ristiintaulukointi toimii yleensä vain kolmiulotteisessa avaruudessa, koska niissä ulottuvuuksissa voidaan mennä ylös tai alas, vasemmalle tai oikealle ja eteen tai taaksepäin.

Etsiä