Vektori: määritelmä, suunta, suuruus ja esimerkit

Vektori on matemaattinen objekti, jolla on koko, jota kutsutaan suuruudeksi, ja suunta. Se esitetään usein lihavoiduilla kirjaimilla (kuten u {\displaystyle \mathbf {u}). } , v {\displaystyle \mathbf {v} }, v {\displaystyle \mathbf {v} } , w {\displaystyle \mathbf {w}). } ), tai suoran segmenttinä pisteestä toiseen (kuten A B → {\displaystyle {\overrightarrow {AB}}} ).

Vektoria käytetään esimerkiksi osoittamaan etäisyyttä ja suuntaa, jossa jokin liikkuu. Kun kysytään suuntaa, jos joku sanoo "Kävele kilometri pohjoiseen", se olisi vektori, mutta jos sanotaan "Kävele kilometri" ilman suuntaa, se olisi skalaari.

Vektorit piirretään yleensä nuolina. Nuolen pituus on verrannollinen vektorin suuruuteen. Suunta, johon nuoli osoittaa, on vektorin suunta.

Määritelmä ja esitys

Vektori voidaan esittää monella tavalla:

• Geometrisesti nuolena, jonka pituus ja suunta kuvaavat vektorin ominaisuuksia.
• Koordinaattimuodossa: esimerkiksi kaksidimensionaalinen vektori v = (v1, v2) tai kolmiulotteinen v = (v1, v2, v3).
• Pisteiden erotuksena: jos A = (x1, y1) ja B = (x2, y2), niin vektori \u2192AB = (x2 - x1, y2 - y1).

Suuruus (normi)

Vektorin suuruus eli pituus merkitään usein |v| tai ||v||. Koordinaateista suuruus lasketaan Pythagoraan lauseen avulla:

• Jos v = (v1, v2), niin |v| = sqrt(v1^2 + v2^2).
• Jos v = (v1, v2, v3), niin |v| = sqrt(v1^2 + v2^2 + v3^2).

Esimerkki: v = (3, 4) ⇒ |v| = 5.

Perusoperaatiot

Vektorien yhteen- ja vähennyslasku: komponenttikohtaisesti. Jos u = (u1, u2) ja v = (v1, v2), niin

u + v = (u1 + v1, u2 + v2), u - v = (u1 - v1, u2 - v2).

Geometrisesti yhteenlasku vastaa nuolien asettamista peräkkäin tai parallelogrammisääntöä.

Skalaaritulo (skalaarilla kertominen): jos k on reaaliluku ja v = (v1, v2), niin k v = (k v1, k v2). Skalaarilla kertominen muuttaa vektorin pituutta ja, jos k < 0, myös suuntaa vastakkaiseksi.

Pistetulo (dot product): kahden vektorin u ja v pistetulo määritellään

u · v = u1 v1 + u2 v2 (+ u3 v3 jos kolmeulotteisissa).

Pistetulon ja suuruuksien avulla u · v = |u||v| cos θ, missä θ on vektorien välinen kulma. Pistetulo kertoo myös vektorien ortogonaalisuuden: u · v = 0 ⇔ vektorit ovat kohtisuorassa.

Ristitulo (kolmiulotteisissa): u × v on vektori, joka on kohtisuorassa sekä u:ta että v:tä vastaan ja jonka suuruus on |u × v| = |u||v| sin θ. Esimerkiksi (1,0,0) × (0,1,0) = (0,0,1).

Yksikkövektori: vektori, jonka suuruus on 1. Jos v ≠ 0, niin yksikkövektori v:n suunnassa on v / |v|.

Vektorien ominaisuuksia

• Vektoreiden yhteenlasku on kommutatiivista ja assosiatiivista: u + v = v + u.
• Skalaaritulo on bilineaarinen ja symmetrinen.
• Nolla-vektori 0 = (0,0,...) on neutraali yhteenlaskussa.
• Negatiivinen vektori -v kääntää suunnan: v + (-v) = 0.
• Kaksi vektoria ovat yhtä suuret ja suuntaiset silloin, kun niiden kaikki komponentit ovat samat.

Esimerkkejä

• Kävely: "Kävele 1 km pohjoiseen" voidaan esittää vektorina (0, 1) (jos yksikkönä km ja pohjoinen +y-suunnassa). "Kävele 1 km" ilman suuntaa on skalaari.
• Koordinaattilasku: u = (1,2), v = (3,-1). Silloin u+v = (4,1), 2u = (2,4).
• Pituuslasku: v = (3,4) ⇒ |v| = sqrt(9+16) = 5.
• Pistetuloesimerkki: (1,2)·(3,4) = 1·3 + 2·4 = 11. Tästä voidaan määrittää vektorien välinen kulma cos θ = (u·v)/(|u||v|).
• Pistetulo nollaa: jos u·v = 0 ja kumpikaan ei ole nolla-vektori, vektorit ovat kohtisuorassa.

Käyttökohteita

Vektoreita käytetään laajasti matematiikassa, fysiikassa ja tekniikassa. Tavallisia sovelluksia ovat:

• Liikkeen kuvaus: nopeus ja kiihtyvyys ovat vektoreita (suuruus + suunta).
• Voimat (esim. Newtonin lait) muodostuvat vektoreista ja summataan vektorioperaatioilla.
• Grafiikka ja tietokonegrafiikka: sijainnin, suunnan ja transformaatioiden käsittely.
• Elektroniikassa ja kenttäteoriassa sähkökentät ja magneettikentät kuvataan vektorikenttinä.

Yhteenveto

Vektori on suuntaan ja suuruuteen liittyvä matemaattinen käsite, jota voi esittää nuolena tai koordinaatteina. Vektoreilla on selkeät laskusäännöt (yhteen- ja vähennyslasku, skalaarikertolasku, pistetulo, ristitulo), ja niiden avulla kuvataan monia reaalimaailman ilmiöitä kuten liikettä ja voimia. Perusajatus on aina sama: vektori kertoo, kuinka paljon ja mihin suuntaan.

Miten lisätä vektoreita

Vektoreiden lisääminen paperille head to tail -menetelmällä

Vektoreiden yhteenlaskumenetelmä Head to Tail on hyödyllinen, kun kahden vektorin yhteenlaskun tulosta arvioidaan paperilla. Näin se tehdään:

• Kukin vektori piirretään nuolena, jonka takana on tietty pituus, jossa jokainen pituusyksikkö paperilla edustaa vektorin tiettyä suuruusluokkaa.
• Piirrä seuraava vektori siten, että toisen vektorin häntä(pää) on ensimmäisen vektorin pään(etuosan) kohdalla.
• Toista tämä kaikille muille vektoreille: Piirrä seuraavan vektorin häntä edellisen vektorin päähän.
• Piirrä viiva ensimmäisen vektorin perästä viimeisen vektorin päähän - se on kaikkien vektoreiden resultantti (summa).

Menetelmää kutsutaan "Head to Tail" -menetelmäksi, koska jokainen edellisen vektorin pää johtaa seuraavan vektorin häntään.

Komponenttilomakkeen käyttäminen

^{[on selitettävä ]}

Komponenttimuodon käyttäminen kahden vektorin lisäämiseen tarkoittaa kirjaimellisesti vektoreiden komponenttien lisäämistä uuden vektorin luomiseksi. Olkoon esimerkiksi a ja b kaksi kaksiulotteista vektoria. Nämä vektorit voidaan kirjoittaa niiden komponenttien avulla.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Oletetaan, että c on näiden kahden vektorin summa, joten c = a + b. Tämä tarkoittaa, että c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Seuraavassa on esimerkki kahden vektorin yhteenlaskusta niiden komponenttimuotojen avulla:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)}

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}}

Tämä menetelmä toimii kaikille vektoreille, ei vain kaksiulotteisille vektoreille.

 
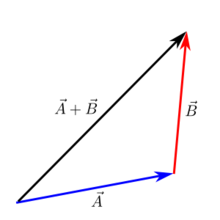
Head-to-tail Lisäys  

Kysymyksiä ja vastauksia

K: Mikä on vektori?

K: Miten vektorit yleensä piirretään?

K: Mitä tarkoittaa, kun joku kysyy suuntaa?

K: Mitä esimerkkejä vektorien käytöstä on?

K: Miten vektorit esitetään matemaattisesti?

K: Mitä tarkoittaa, kun jotain asiaa kutsutaan skalaariksi?

Hae kirjaimella