Sylinteri: määritelmä, pinta-ala, tilavuus ja tyypit

Sylinteri – selkeä määritelmä, laskut pinta-alalle ja tilavuudelle sekä esimerkit ja erot elliptiseen, parabolisiseen ja hyperboliseen sylinteriin.

Tekijä: Leandro Alegsa

09-01-2026 21:23

Sylinteri on yksi yksinkertaisimmista kaarevista kolmiulotteisista geometrisista muodoista, jonka pinnan muodostavat pisteet, jotka ovat kiinteällä etäisyydellä tietystä viivapätkästä, jota kutsutaan sylinterin akseliksi. Muoto voidaan ajatella pyöreäksi prismaksi. Sekä pintaa että sen sisällä syntyvää kiinteää muotoa voidaan kutsua sylinteriksi. Sylinterin pinta-ala ja tilavuus on tunnettu jo antiikin ajoista lähtien.

Differentiaaligeometriassa sylinteri määritellään laajemmin säännellyksi pinnaksi, jonka välissä on yhden parametrin mittainen yhdensuuntaisten viivojen perhe. Sylinteriä, jonka poikkileikkaus on ellipsi, paraabeli tai hyperbeli, kutsutaan vastaavasti elliptiseksi sylinteriksi, paraboliseksi sylinteriksi tai hyperboliseksi sylinteriksi.

Määritelmä ja peruskäsitteet

Sylinteri on kolmiulotteinen kappale, jonka muodostavat kaksi kongruenttia, toisiaan vastakkaista pohjatasoa (esim. ympyrät) ja niiden välinen sivupinta, joka koostuu pohjien reunojen yhdistämistä suoran viivan kappaleista (generaatio- tai muodostusviivoista). Tärkeimmät termit:

Pohja — sylinterin kummankin pään taso, usein ympyrä tai muu suljettu käyrä.
Akseli — suora, joka yhdistää pohjien keskikohdat; oikea (suora) sylinteri tarkoittaa, että akseli on kohtisuorassa pohjia vastaan, vinossa (oblique) akseli ei ole.
Korkeus (h) — etäisyys pohjien tasojen välillä mitattuna akselin suuntaisesti (eli lyhin etäisyys pohjien välillä).
Generaattori — sivupinnan muodostavat suorat viivat, jotka ovat yhdensuuntaisia akselin kanssa.

Oikea ympyräsylinteri — pinta-ala ja tilavuus

Useimmin käsitelty sylinteri on oikea ympyräsylinteri, jonka pohjat ovat ympyröitä säteellä r ja korkeus h. Tärkeimmät kaavat:

Pohjan ala: A_pohja = π r²
Vastaavan ympyrän kehä (pohjan ympärysmitta): P = 2 π r
Sivupinnan ala (vaippa): A_vaippa = 2 π r h — vaippa voidaan "avata" suorakaiteeksi, jonka korkeus on h ja leveys on pohjan kehä 2πr.
Kokonaispinta-ala: A_kok = 2 π r (r + h) = 2·A_pohja + A_vaippa
Tilavuus: V = π r² h = A_pohja · h

Yksinkertainen numeerinen esimerkki: jos r = 3 (yksikköä) ja h = 5 (yksikköä), niin V = π·3²·5 = 45π ≈ 141,37 (yksikköä³).

Oblique (vino) sylinteri ja yleisempi päättely

Vinon sylinterin pohjat ovat samanlaiset käyrät kuin suorassa tapauksessa, mutta akseli ei ole kohtisuorassa pohjaa vastaan. Tärkeä ominaisuus: vinon sylinterin tilavuus lasketaan samalla kaavalla kuin suoralla sylinterillä — tilavuus on aina pohjan ala kertaa korkeus (pohjaan nähden mitattu normaali etäisyys): V = A_pohja · h. Tämä seuraa Cavalierin periaatteesta sekä integraalilaskennasta.

Muunnokset ja erityistyypit

Elliptinen sylinteri: pohjana ellipsi. Tilavuus V = (π a b) h, missä a ja b ovat ellipsin puolisuakset.
Parabolinen ja hyperbolinen sylinteri: pohjakäyränä paraabeli tai hyperbeli — kyseessä on säännöllinen yhdensuuntaisten viivojen perhe, ja pinnan geometriikka eroaa ympyräsylinteristä.
Koteloitu (putkimainen) sylinteri: sylinterirengas, jolla on ulkokehän säde R ja sisäkehän säde r. Tilavuus V = π (R² − r²) h. Kokonaispinta-ala sisältää ulko- ja sisäpinnan sekä päätyrenkaat.
Kupsu tai katkaistu sylinteri: esimerkiksi sylinterin leikkaus vinoon tasoon tuottaa erilaisia leikkauksia (ellipsat, paraabelat jne.).

Geometrinen ja differentiaali-geometrinen näkökulma

Kuten alkuperäisessä tekstissä mainittiin, differentiaaligeometriassa sylinteri voidaan määritellä säännölliseksi pinnaksi, jolla on yhden parametrin mittainen yhdensuuntaisten viivojen perhe. Oikean ympyräsylinterin parametriesitys tavallisesti käytetyssä koordinaatistossa on

(x, y, z) = (r cos θ, r sin θ, z), missä θ ∈ [0, 2π) ja z ∈ [0, h].

Tällainen parametriesitys on hyödyllinen pinnan pinta-alan laskuissa ja pintaintegraaleissa.

Sovelluksia ja historiallinen huomautus

Sylintereitä esiintyy laajasti luonnossa ja tekniikassa: putket, säiliöt, pyörivien kappaleiden runkot, moottorin männät ja monet muut rakenteet. Antiikin ja renessanssin matemaatikot tunsivat sylinterin pinta-alan ja tilavuuden laskut. Arkhimedes vertasi kuulaa ja sitä ympäröivää sylinteriä ja löysi kuulalle ja sitä ympäröivälle sylinterille mielenkiintoisia suhdelukuja (esimerkiksi pallon tilavuus on 2/3 sitä ympäröivän sylinterin tilavuudesta).

Yhteenveto

Sylinterin perusominaisuudet määräytyvät pohjakäyrän ja akselin (korkeuden) mukaan.
Oikean ympyräsylinterin tilavuus on V = π r² h ja kokonaispinta-ala A = 2 π r (r + h).
Vinon sylinterin tilavuus on sama kuin vastaavan suoran sylinterin — aina pohjan ala kertaa korkeus.
Erilaiset poikkileikkaukset (ellipsi, paraabeli, hyperbeli) johtavat elliptisiin, parabolisiiin ja hyperbolisiin sylintereihin, joita tutkitaan sekä klassisessa geometriassa että differentiaaligeometriassa.

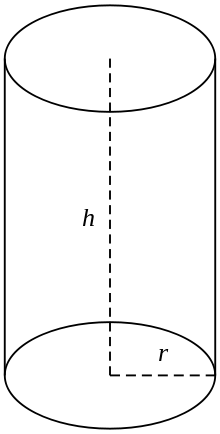
Suoraan ympyränmuotoinen sylinteri

Yleinen käyttö

Yleisessä käytössä sylinterillä tarkoitetaan suorakulmaisen ympyräsylinterin äärellistä poikkileikkausta, eli sylinteriä, jonka muodostavat viivat ovat kohtisuorassa perustuksia vastaan ja jonka päät on suljettu siten, että ne muodostavat kaksi ympyränmuotoista pintaa, kuten kuvassa (oikealla). Jos sylinterin säde $on r$ ja pituus (korkeus) h, sen tilavuus saadaan seuraavasti:

$V$ $= πr 2 h$

ja sen pinta-ala on:

yläosan pinta-ala $(πr 2) +$
pohjan pinta-ala $(πr 2) +$
sivun pinta-ala ( $2πrh$ ).

Ilman ylä- tai alapuolta (sivualue) pinta-ala on siis:

$A$ $= 2πrh$ .

Ylä- ja alapuolella pinta-ala on:

$A$ $= 2πr 2 + 2πrh = 2πr(r + h)$ .

Tietyn tilavuuden tapauksessa sylinterin, jonka pinta-ala on pienin, pinta-ala on $h = 2r$ . Tietyn pinta-alan tapauksessa sylinterin, jonka tilavuus on suurin, $h = 2r, eli$ sylinteri mahtuu kuutioon (korkeus = halkaisija).

Volume

Kun on oikeanmuotoinen ympyränmuotoinen sylinteri, jonka korkeus on $h$ yksikköä ja jonka pohjan säde on $r$ yksikköä ja jonka koordinaattiakselit on valittu siten, että origo on yhden pohjan keskipisteessä ja korkeus mitataan positiivista x-akselia pitkin. Tasoleikkauksen, joka on $x$ yksikön etäisyydellä origosta, pinta-ala on $A (x)$ neliöyksikköä, jossa

A ( x ) = π r 2 {\displaystyle A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

tai

A ( y ) = π r 2 {\displaystyle A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Tilavuuselementti on suorakulmainen sylinteri, jonka pohjapinta-ala on $Aw i$ neliöyksikköä ja paksuus $Δ i x$ yksikköä. Jos siis V kuutiota on oikean ympyränmuotoisen sylinterin tilavuus, Riemannin summien mukaan,

V o l u m e o f c y l i n d e r = lim | | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{||\\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π r 2 d y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Lieriökoordinaattien avulla tilavuus voidaan laskea integroimalla yli

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Lieriömäinen poikkileikkaus

Sylinterileikkaukset ovat sylinterien ja tasojen leikkauspisteitä. Suoraan ympyränmuotoisen sylinterin kohdalla on neljä vaihtoehtoa. Sylinterin tangenttitaso kohtaa sylinterin yhtenä suorana. Jos tasoa liikutetaan sen ollessa samansuuntainen itsensä kanssa, se joko ei leikkaa sylinteriä tai leikkaa sen kahdella samansuuntaisella suoralla. Kaikki muut tasot leikkaavat sylinterin ellipsinä tai, jos ne ovat kohtisuorassa sylinterin akselia vastaan, ympyränä.

Muut sylinterityypit

Elliptinen sylinteri eli cylindroid on kvadrinen pinta, jolla on seuraava yhtälö kartesiankoordinaatistossa:

( x a ) 2 + ( y b ) 2 = 1. {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Tämä yhtälö koskee elliptistä sylinteriä, joka on tavallisen ympyränmuotoisen sylinterin ( $a = b$ ) yleistys. Vielä yleisempi on yleistetty sylinteri: poikkileikkaus voi olla mikä tahansa käyrä.

Sylinteri on degeneroitunut nelikulmio, koska ainakin yksi koordinaateista (tässä tapauksessa $z)$ ei esiinny yhtälössä.

Vinosylinterin ylä- ja alapinnat ovat siirtyneet toisistaan.

On myös muita epätavallisempia sylinterityyppejä. Nämä ovat kuvitteellisia elliptisiä sylintereitä:

( x a ) 2 + ( y b ) 2 = - 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1}} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

hyperbolinen sylinteri:

( x a ) 2 - ( y b ) 2 = 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

ja parabolinen sylinteri:

x 2 + 2 a y = 0. {\displaystyle x^{2}+2ay=0.\,} $x^{2}+2ay=0.\,$

↑"MathWorld: WorldWorld: Lieriömäinen poikkileikkaus".

Elliptinen sylinteri

Projektiivisessa geometriassa sylinteri on yksinkertaisesti kartio, jonka kärki on äärettömässä, mikä vastaa visuaalisesti perspektiivistä katsottuna sylinteriä, joka näyttää olevan kartio taivasta kohti.

Kysymyksiä ja vastauksia

K: Mikä on sylinteri?

A: Sylinteri on kolmiulotteinen geometrinen muoto, jonka pinnan muodostavat pisteet, jotka ovat kiinteällä etäisyydellä tietystä viivapätkästä, jota kutsutaan sylinterin akseliksi. Sitä voidaan ajatella ympyränmuotoisena prismana, ja sekä pintaa että sen sisällä syntyvää kiinteää muotoa voidaan kutsua sylinteriksi.

Kysymys: Kuinka kauan ihmiset ovat tienneet sylinterien pinta-alasta ja tilavuudesta?

V: Lieriöiden pinta-ala ja tilavuus on tunnettu jo antiikin ajoista lähtien.

K: Mitä ovat elliptinen, parabolinen ja hyperbolinen sylinteri?

V: Elliptiset, paraboliset ja hyperboliset sylinterit ovat sylintereitä, joiden poikkileikkaus on vastaavasti ellipsi, paraabeli tai hyperbeli.

K: Miten sylinteri määritellään differentiaaligeometriassa?

V: Differentiaaligeometriassa sylinteri määritellään laajemmin säännönmukaiseksi pinnaksi, jonka välissä on yhden parametrin mittainen yhdensuuntaisten viivojen perhe.

K: Mitä tarkoittaa, että jokin on "hallittu"?

V: "Hallittu" tarkoittaa, että siihen on piirretty suorat viivat tavalla tai toisella.

Kysymys: Onko olemassa vain yhdenlaista sylinteriä?

V: Ei, on olemassa monia erilaisia sylinterityyppejä, kuten elliptisiä, parabolisia ja hyperbolisia sylintereitä, joilla kaikilla on erilainen poikkileikkaus.

Etsiä