Impedanssi – määritelmä, kaavat, taajuusvaikutus ja ero resistanssiin

Impedanssi — selkeä määritelmä, tärkeimmät kaavat, taajuusvaikutus ja ero resistanssiin. Opas induktoreihin, kondensaattoreihin, laskuihin ja käytännön esimerkkeihin.

Tekijä: Leandro Alegsa

15-01-2026 22:04

Sähköinen impedanssi kuvaa, kuinka paljon virtapiiri vastustaa vaihtovirran (tai vaihtuvan jännitteen) muutosta. Impedanssi on yleinen laajennus resistanssille, joka ottaa huomioon myös komponenttien reaktiivisen käyttäytymisen (induktio ja kapasitanssi) ja sen, että vastus voi olla kompleksiluku, jolla on sekä suuruus että vaihe.

Kaksi yleistä tapaa esittää impedanssi ovat:

resistanssi "R" (reaaliosa) ja reaktanssi "X" (imaginääriosa), esimerkiksi Z = 1 + 1 j {\displaystyle Z=1+1j} $Z=1+1j$
esitys suuruuden ja vaiheen avulla (kompleksiluku polaarimuodossa), eli suuruus |Z| ja kulma ∠θ. Esimerkiksi Z = 1.4 $Z=1.4\angle 45^{\circ }$ (1,4 ohmia 45 asteen kulmassa)

Tulkinta ja peruskaavat

Impedanssi Z on kompleksiluku, joka voidaan kirjoittaa suorakulmaisena muodossa Z = R + jX, missä R on resistanssi (reaaliosa) ja X on reaktanssi (imaginääriosa). Polaarimuodossa Z = |Z| ∠θ, missä |Z| = sqrt(R² + X²) ja θ = arctan(X/R) (oikea kvadrantti huomioiden).

Resistanssin (puhtaan R) käyttäytyminen kuvaa ohmin lakia: V = R ∗ I {\displaystyle V=R*I} $V=R*I$ , eli mitä suurempi vastus, sitä suurempi tarvittava jännite tietylle virralle.

Impedanssin tapauksessa käytetään vastaavaa kompleksimuotoista suhdetta phasoreille: V = Z ∗ I {\displaystyle V=Z*I} $V=Z*I$ , missä V ja I ovat ajoittain muuttuvien signaalien kompleksifaasoreita (amplitudi ja vaihe).

Induktori ja kondensaattori — taajuusriippuvuus

Impedanssit vaihtelevat taajuuden f mukaan. Taajuus f kertoo, kuinka monta kertaa sekunnissa signaalin suunta vaihtuu.

Induktorin impedanssi:

Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} $Z=j2\pi fL\,$ . Tässä j on imaginaariyksikkö, π on pi, f on taajuus ja L induktanssi. Induktorin reaktanssi X_L = 2πfL on positiivinen, eli Z_L = jX_L.

Kondensaattorin impedanssi:

Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} $Z={\frac {1}{j2\pi fC}}$ . Tämä voidaan myös kirjoittaa Z_C = -j/(2πfC), eli kondensaattorin reaktanssi X_C = -1/(2πfC) on negatiivinen.

Näin ollen:

DC (f = 0): induktorin impedanssi Z_L = 0 (oikosulku matalilla taajuuksilla), kondensaattorin impedanssi Z_C → ∞ (avopiiri DC:ssä).
Korkeilla taajuuksilla: induktorin impedanssi kasvaa (se estää nopeita muutoksia), kondensaattorin impedanssi pienenee (se päästää korkeataajuisia komponentteja helpommin läpi).

Fyysinen tausta ja energian käsittely

Yksinkertaistettuna:

vastus aiheuttaa häviötä: elektronit törmäävät atomien kanssa ja energia häviää lämmöksi;
kondensaattori varastoi energiaa sähkökenttään;
induktori varastoi energiaa magneettikenttään.

Tämän vuoksi vastus muuntaa sähköenergiaa pysyvästi lämmöksi, kun taas kondensaattori ja induktori voivat varastoida energiaa ja palauttaa sen myöhemmin takaisin piiriin.

Verkkoelementtien yhdistäminen ja muotoilu

Yksinkertaisia yhdistelysääntöjä:

Sarjakytkennässä impedanssit summautuvat: Z_total = Z1 + Z2 + ...
Rinnankytkennässä kokonaisimpedanssi saadaan käyttämällä admittanssia Y = 1/Z: Y_total = Y1 + Y2 + ... ja Z_total = 1 / Y_total.

Heijastukset ja aaltoliikkeet

Kun lähteen, kaapelin (tai siirtolinjan) ja kuorman impedanssit eivät täsmää, osa signaalin energiasta heijastuu takaisin. Heijastuskerroin Γ lasketaan:

Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}} $\Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}$ ,

missä Z_S on lähteen impedanssi ja Z_L kuorman impedanssi. Jos Z_L = Z_S, heijastusta ei synny (Γ = 0) ja siirto on optimaalinen.

Kaikilla aaltoliikkuvilla väliaineilla on oma aaltoimpedanssinsa. Esimerkiksi tyhjä avaruus (vapaan tilan ominaisimpedanssi) on noin 377 Ω. $\Omega$

Yksittäisen impedanssin suuruus ja vaihe

Jos Z = R + jX, niin impedanssin suuruus ja vaihe ovat:

|Z| = sqrt(R² + X²)
θ = arctan2(X, R) (käyttämällä arctan2-funktiota oikean kulman saamiseksi)

Esimerkiksi Z = 1 + j1 vastaa polaarimuodossa |Z| ≈ 1.414 ja kulmaa 45° (esitetty aiemmin kuvana $Z=1.4\angle 45^{\circ }$ ).

Käytännön sovelluksia

Impedanssin ymmärtäminen on keskeistä mm. seuraavissa tilanteissa:

signaalinsiirrossa ja antennien suunnittelussa (säätö oikeaan aallonvastukseen vähentää heijastuksia);
suodattimien ja resonanssipiirien (esim. LC-suodattimet) suunnittelussa, joissa taajuusriippuvuus hyödynnetään;
virtalähteiden ja kuormien yhteensovittamisessa; sekä
tehopiireissä, joissa mitataan aktiivista, reaktiivista ja näennäistä tehoa (kompleksiteho).

Lyhyesti: impedanssi laajentaa resistanssin käsitettä ottamalla huomioon sekä energian häviöt että energian varastoinnin vaikutukset riippuvaisina taajuudesta ja vaiheesta.

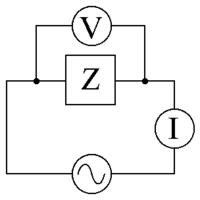
Vaihtovirtalähde, joka syöttää jännitteen V {\displaystyle \scriptstyle V} $\scriptstyle V$ impedanssin Z {\displaystyle \scriptstyle Z} yli. $\scriptstyle Z$ , joka ohjaa virtaa I {\displaystyle \scriptstyle I} $\scriptstyle I$

Signaali heijastuu osittain takaisin, kun impedanssi muuttuu.

Kompleksisen impedanssitason graafinen esitys

Vaihe

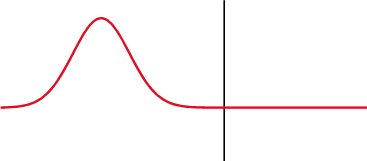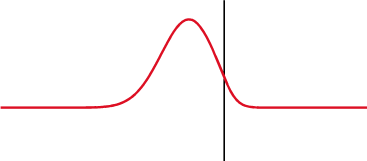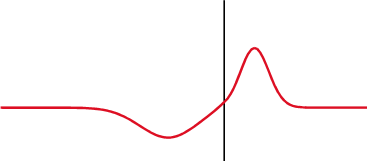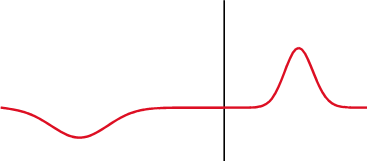
Vastuksen yli sekä jännite että virta nousevat ja laskevat samanaikaisesti, niiden sanotaan olevan samassa vaiheessa, mutta impedanssin kanssa tilanne on erilainen, jännite siirtyy 1/4 aallonpituudella kondensaattorissa virran taakse ja induktorissa eteenpäin.

1/4 aallonpituus esitetään yleensä imaginääriluvulla "j", joka vastaa myös 90 asteen siirtymää.

Kuvitteellisen luvun "j" käyttö tekee matematiikasta paljon yksinkertaisempaa, sillä sen avulla voidaan laskea kokonaisimpedanssi samalla tavalla kuin se tehdään vastusten kanssa, esimerkiksi vastus plus impedanssi sarjassa on R+Z, ja rinnakkain se on (R*Z)/(R+Z).

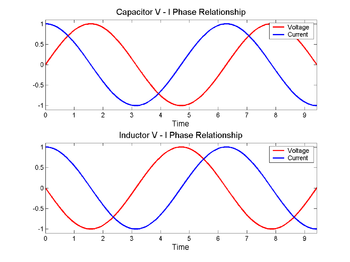
Kondensaattorin yli (ylhäällä) jännite (punainen) muuttuu virran (sininen) jälkeen, induktorin yli (alhaalla) ennen sitä. Jännitteen ja virran vaihe-ero on 1/4 aallonpituutta.

Kysymyksiä ja vastauksia

K: Mikä on sähköinen impedanssi?

V: Sähköinen impedanssi on virtapiirin vastuksen määrä virran tai jännitteen muutokselle.

K: Miten sähköinen impedanssi voidaan kirjoittaa?

V: Sähköinen impedanssi voidaan kirjoittaa resistanssilla "R" (reaaliosa) ja reaktanssilla "X" (imaginääriosa) sekä suuruudella, vaiheella, koolla ja kulmalla.

K: Mitä eroa on resistanssin ja impedanssin välillä?

V: Resistanssin ja impedanssin keskeinen ero on sana "muutos"; toisin sanoen muutosnopeus vaikuttaa impedanssiin. Resistanssi vastustaa sen läpi kulkevaa virtaa, kun taas induktori vastustaa virran muutoksia ja kondensaattori vastustaa jännitteen muutoksia.

Kysymys: Mitkä ovat resistanssiin ja impedanssiin liittyviä kaavoja?

V: Resistanssin osalta V=R*I, jossa V on jännite, R on resistanssi ja I on virta; induktoreiden osalta Z=j2πfL; kondensaattoreiden osalta Z=1/j2πfC; jossa Z edustaa impedanssia, j edustaa mielikuvituslukua -1 , π edustaa vakiota pi, f edustaa taajuutta, L edustaa induktanssia ja C edustaa kapasitanssia.

Kysymys: Mitä fysikaalisia selityksiä on resistanssin ja impedanssin väliselle suhteelle?

V: Resistanssi aiheutuu elektronien törmäämisestä vastusten sisällä oleviin atomeihin, kun taas induktorin impedanssi syntyy sähkökentän luomisesta ja kondensaattorin impedanssi syntyy magneettikentän luomisesta. Lisäksi vastukset hukkaavat energiaa, kun taas induktorit ja kondensaattorit varastoivat energiaa, joka voidaan sitten palauttaa lähteeseen, kun se laskee.

K: Miten lasketaan heijastuskerroin?

V: Heijastuskerroin voidaan laskea käyttämällä Γ=(ZL-ZS)/(ZL+ZS), jossa Γ (iso gamma) tarkoittaa heijastuskerrointa; ZS tarkoittaa lähteen impedenssiä; ZL tarkoittaa kuorman impedenssiä.

Etsiä