Fourier-muunnos: määritelmä, kaava ja käytännön sovellukset
Fourier-muunnos — selkeä määritelmä, keskeinen kaava ja käytännön sovellukset äänen analyysistä koneoppimiseen ja kvanttifysiikkaan.
Fourier-muunnos on matemaattinen funktio, jonka avulla voidaan löytää aallon perustaajuudet. Kuvittele, että soitat sointua pianolla. Soitettaessa soinnun nuottien äänet sekoittuvat yhteen ja muodostavat ääniaallon. Tämä toimii, koska jokaisen eri nuotin aallot häiritsevät toisiaan laskemalla yhteen tai kumoamalla ne aallon eri kohdissa. Fourier-muunnos ottaa tämän kompleksisen aallon ja pystyy löytämään sen muodostaneet taajuudet, mikä tarkoittaa, että sillä voidaan löytää nuotit, joista sointu on muodostettu.
Fourier-muunnoksen ulostuloa kutsutaan toisinaan taajuusspektriksi tai -jakaumaksi, koska se näyttää syötteen mahdollisten taajuuksien jakauman. Tätä funktiota käytetään moniin tarkoituksiin kryptografiassa, valtameritutkimuksessa, koneoppimisessa, radiologiassa, kvanttifysiikassa sekä äänisuunnittelussa ja visualisoinnissa.
Funktion Fourier-muunnos 

missä:
on taajuus.
on Fourier-muunnosfunktio, ja se palauttaa arvon, joka kuvaa sitä, kuinka yleinen taajuus
on alkuperäisessä signaalissa.
edustaa tuloaaltofunktion
käärimistä kompleksitason origon ympäri jollakin taajuudella
.
Käänteinen Fourier-muunnos saadaan seuraavasti
Fourier-muunnos osoittaa, mitä taajuuksia signaalissa on. Tarkastellaan esimerkiksi ääniaaltoa, joka sisältää kolme erilaista nuottia: Kun teet kuvaajan tämän ääniaallon Fourier-muunnoksesta (jossa taajuus on x-akselilla ja voimakkuus y-akselilla), näet piikin kullakin taajuudella, joka vastaa yhtä nuotista.
Monia signaaleja voidaan luoda laskemalla yhteen kosinuksia ja sinuksia, joiden amplitudi ja taajuus vaihtelevat. Fourier-muunnos esittää näiden kosinusten ja sinien amplitudit ja vaiheet suhteessa niiden taajuuksiin.
Fourier-muunnokset ovat tärkeitä, koska monista signaaleista saa enemmän tolkkua, kun niiden taajuudet erotetaan toisistaan. Yllä olevassa ääniesimerkissä signaalin tarkastelu ajan suhteen ei tee selväksi, että signaalissa ovat sävelet A, B ja C. Monet järjestelmät tekevät eri asioita eri taajuuksille, joten tällaisia järjestelmiä voidaan kuvata sen mukaan, mitä ne tekevät kullekin taajuudelle. Esimerkki tästä on suodatin, joka estää korkeat taajuudet.
Fourier-muunnoksen laskeminen edellyttää integroinnin ja imaginäärilukujen ymmärtämistä. Fourier-muunnosten laskemiseen käytetään tavallisesti tietokoneita vain yksinkertaisimmissa signaaleissa. Nopea Fourier-muunnos on menetelmä, jota tietokoneet käyttävät Fourier-muunnoksen nopeaan laskemiseen.
· 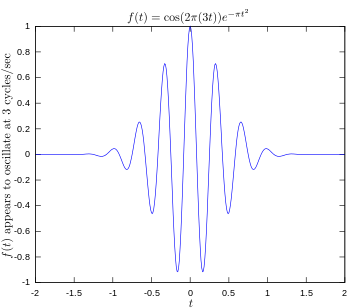
Alkuperäinen funktio, jossa näkyy 3 hertsin taajuudella värähtelevä signaali.
· 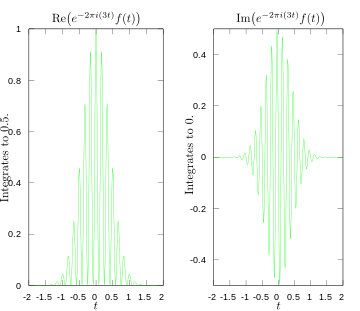
Integraatin reaali- ja imaginaariosat Fourier-muunnoksessa 3 hertsin taajuudella
· 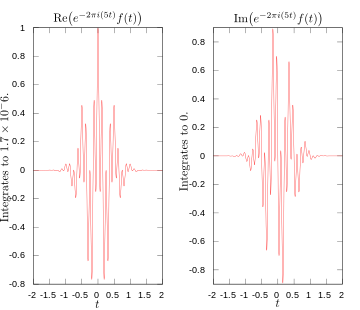
Integraatin reaali- ja imaginääriosat Fourier-muunnoksessa 5 hertsin taajuudella
· 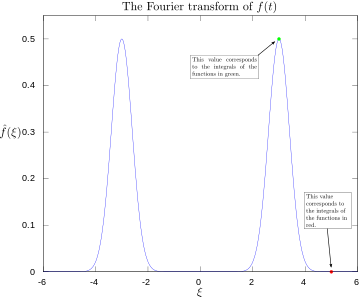
Fourier-muunnos, jossa 3 ja 5 hertsiä merkitty.
Perusominaisuudet ja hyödylliset kaavat
Fourier-muunnoksella on useita käteviä ominaisuuksia, joita käytetään analyysissa ja sovelluksissa:
- Lineaarisuus: F{af + bg} = a F{f} + b F{g}.
- Siirto (time shift): Jos g(x)=f(x-x0), niin G(α)=e^{-2π i α x0} F(α).
- Modulaatio (frequency shift): Jos g(x)=e^{2π i α0 x} f(x), niin G(α)=F(α-α0).
- Skalointi: Jos g(x)=f(ax), niin G(α)= (1/|a|) F(α/a) (riippuu normalisointikonventiosta).
- Derivointi: Derivaatta ajassa vastaa kertomista taajuustasossa: F{f'}(α) = (2π i α) F(α).
- Konvoluutioteoreema: F{f * g} = F{f} · F{g} ja F{f · g} = F{f} * F{g}. Tämä on erittäin hyödyllinen suodatus- ja järjestelmäanalyysissä.
- Parseval / Plancherel: Energian säilyvyys: integraali |f(x)|^2 dx = integraali |F(α)|^2 dα (riippuu normalisoinnista).
Milloin Fourier-muunnos on olemassa?
Jotta tavanomainen integraalimuotoinen Fourier-muunnos F(α)=∫_{-∞}^{+∞} f(x) e^{-2π i α x} dx olisi suoraan määritelty, tarvitaan esimerkiksi, että f on L1-funktio (eli integraali |f(x)| dx on äärellinen). Monissa tärkeissä tapauksissa (esim. neliöintegroinnit) käytetään Plancherelin teoreemaa ja L2-funktioita, ja joskus täytyy käsitellä yleisempiä jakeluita (distribution), kuten Diracin deltaa.
Diskreetti Fourier-muunnos ja Nopea Fourier-muunnos (FFT)
Käytännössä mittaukset ja tietokonesimuloinnit ovat diskreettejä. Jos tarkastelet N näytettä f[n] (n=0,...,N-1), määritellään diskreetti Fourier-muunnos (DFT) muodossa
F[k] = ∑_{n=0}^{N-1} f[n] e^{-2π i k n / N}, k=0,...,N-1
DFT laskee N kompleksiarvoista taajuuskomponenttia ja sen käänteinen muunnos palauttaa näytesignaalin. Nopea Fourier-muunnos (FFT) on tehokas algoritmi DFT:n laskemiseen aikavaativuudella O(N log N) verrattuna suoraan O(N^2):een.
Näytteenotto, Aliasing ja Nyquist
Käytännön signaalinkäsittelyssä jatkuva signaali näytetään diskreetisti näytetaajuudella Fs. Näytteenoton perussääntö (Nyquist) sanoo, että jos signaali sisältää taajuuksia vain alle Fs/2, se voidaan rekonstruoida täydellisesti. Jos korkeammat taajuudet ovat läsnä, tapahtuu aliasointi: korkeammat taajuudet näyttävät matalammilta taajuuksilta diskreetissä spektrissä. Tämän vuoksi usein käytetään anti-alias-suodattimia ennen näytteenottoa.
Ajan ja taajuuden tarkastelun rajoitukset
Fourier-muunnos antaa täydellisen kuvan taajuuksista, mutta menettää ajallisen sijainnin (missä tietyt taajuudet esiintyvät). Tämä johtaa ajan–taajuuden kompromissiin: jos halutaan tietää sekä taajuudet että niiden esiintymisajankohdat, käytetään muun muassa lyhytaikaista Fourier-muunnosta (STFT) tai aaltomuunnoksia (wavelets).
Yleisiä sovelluksia
- Äänianalyysi ja musiikkiteknologia: sävelkorkeuden tunnistus, äänisuodatus, äänenparannus.
- Kuvan käsittely: 2D-Fourier-muunnos kuvien suodattamiseen, terävöitykseen ja rekonstruointiin.
- Langattomat yhteydet ja signaalinkäsittely: modulaatio, kanavanmallinnus ja suodatus.
- MRI ja tomografia: Fourier-muunnosta käytetään mittaustietojen muuntamiseen kuvaksi.
- Differential equations: differentiaaliyhtälöiden ratkaiseminen taajuustasossa on usein helpompaa.
- Analytiikka ja koneoppiminen: piirteiden erotus ja spektriominaisuuksien hyödyntäminen.
Numerisia huomioita ja käytännön vinkkejä
- Nollatäydennys (zero-padding): lisää resoluutiota taajuustasossa interpoloimalla spektriä (ei tuo uutta informaatiota, mutta auttaa visualisoinnissa).
- Ikkunointi: kun analysoidaan osaa pitkästä signaalista, käytetään ikkunoita (Hann, Hamming jne.) vähentämään spektreihin tulevaa vuotoa (spectral leakage).
- Diskreetti aikasarja: huolehdi, että ikkunan pituus ja näytetiheys sopivat haluttuun taajuusresoluutioon ja aikaresoluutioon.
- Pyöristys- ja tarkkuusongelmat: suurissa FFT-laskuissa huomioi numeerinen vakaus ja liukulukutarkkuus.
Esimerkkejä
Yksinkertainen esimerkki: siniaalto f(t)=sin(2π·3 t) näkyy Fourier-spektrissä piikkinä taajuudella 3 Hz. Tämä on juuri kuvatun esimerkin idea, ja edellä olevat kuvat havainnollistavat tätä: integraalin reaali- ja imaginaariosat tuovat yhteen muodostuvan amplitudin kullekin taajuudelle.
Toinen tärkeä tulos: Gaussin funktion FT on myös Gaussin muotoinen. Tämä tekee Gaussian sopivaksi ikkuna- ja analyysifunktioksi monissa tapauksissa.
Yhteenveto
Fourier-muunnos on keskeinen työkalu signaalien, kuvien ja fysikaalisten ilmiöiden analyysissä. Se muuntaa ajan (tai avaruuden) riippuvan signaalin taajuustasoksi, paljastaen piirteitä, joita on vaikea havaita suoraan ajassa. Käytännössä jatkuvan Fourier-muunnoksen rinnalla käytetään diskreettiä muotoa (DFT) ja sen tehokasta laskentamenetelmää FFT:tä. Kun huomioidaan näytteenoton, ikkunoiden ja numeriikan rajoitukset, Fourier-tekniikat ovat erittäin tehokkaita ja laajasti käytössä eri tieteenaloilla.
Aiheeseen liittyvät sivut
- Fourier-analyysi
- Fourierin inversioteoria
- Fourier-sarja
- Laplace-muunnos
Kysymyksiä ja vastauksia
K: Mikä on Fourierin muunnos?
A: Fourier-muunnos on matemaattinen funktio, jonka avulla voidaan löytää perustaajuudet, joista aalto koostuu. Se ottaa kompleksisen aallon ja löytää sen muodostavat taajuudet, minkä avulla voidaan tunnistaa soinnun muodostavat nuotit.
Kysymys: Mihin tarkoituksiin Fourier-muunnosta käytetään?
V: Fourier-muunnoksella on monia käyttötarkoituksia kryptografiassa, valtameritutkimuksessa, koneoppimisessa, radiologiassa, kvanttifysiikassa sekä äänisuunnittelussa ja visualisoinnissa.
K: Miten Fourier-muunnos lasketaan?
V: Funktion f(x) Fourier-muunnos saadaan kaavalla F(ב) = ∫-∞+∞f(x)e-2נiבxdx missä ב on taajuus. Tämä palauttaa arvon, joka kuvaa, kuinka yleinen taajuus ב on alkuperäisessä signaalissa. Käänteinen Fourier-muunnos on f(x) = ∫-∞+∞F(ב)e+2נixבdב.
Kysymys: Miltä näyttää Fourier-muunnoksen ulostulo?
V: Fourier-muunnoksen tulosta voidaan kutsua joko taajuusspektriksi tai jakaumaksi, koska se näyttää syötteen mahdollisten taajuuksien jakauman.
K: Miten tietokoneet laskevat nopeita Fourier-muunnoksia?
V: Tietokoneet käyttävät algoritmia nimeltä Fast Fourier Transform (FFT) laskeakseen nopeasti kaikki muut kuin yksinkertaisimpien signaalien muunnokset.
K: Mitä signaalien tarkastelu ajan suhteen ei näytä meille?
V: Kun tarkastellaan signaaleja ajan suhteen, ei käy ilmi, mitä ääniä niissä on; monista signaaleista saa enemmän tolkkua, kun niiden taajuudet erotetaan toisistaan ja analysoidaan erikseen.
Etsiä

