Pii (vakio) | matemaattinen vakio, joka on ympyrän ympärysmitan ja halkaisijan suhde

Fundamentals

Määritelmä

π määritellään yleisesti ympyrän kehän C ja halkaisijan d suhteena:

π = C d . {\displaystyle \pi ={\frac {C}{d}}.}

Arvioitu arvo

Pi kirjoitetaan usein π:llä tai kreikkalaisella π-kirjaimella lyhenteenä. Pi on myös irrationaaliluku, eli sitä ei voi kirjoittaa murtolukuna ( a b {\displaystyle a \over b} ), jossa a ja b ovat kokonaislukuja. Tämä tarkoittaa periaatteessa sitä, että desimaaliluvun oikealla puolella olevat pi:n numerot jatkuvat ikuisesti toistumatta kaavassa ja että pi:n tarkkaa arvoa on mahdotonta kirjoittaa lukuna. Pi voidaan vain approksimoida tai mitata arvoksi, joka on riittävän lähellä käytännön tarkoituksia varten.

Pi:tä lähellä oleva arvo on 3.141592653589793238462643... Pi:n yleinen murtolukujen approksimaatio on 22/7 {\displaystyle 22/7}. , jolloin saadaan noin 3,14285714. Tämä approksimaatio on 0,04 %:n päässä pi:n todellisesta arvosta. Vaikka tämä approksimaatio hyväksytään suurimmaksi osaksi tosielämässä, murtoluku 355 / 113 {\displaystyle 355/113} on tarkempi (antaa noin 3,14159292), ja sitä voidaan käyttää silloin, kun tarvitaan lähempänä piitä oleva arvo. Tietokoneiden avulla voidaan saada parempia approksimaatioita piille.

Maaliskuussa 2019 Emma Haruka Iwao laski pi:n arvon 31,4 biljoonaan numeroon.

 
Ympyrän kehä on hieman yli kolme kertaa sen halkaisijan pituinen. Tarkkaa suhdetta kutsutaan π:ksi .  


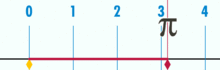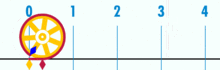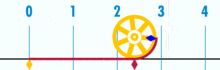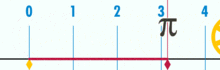
Kaavio, josta näkyy, miten π voidaan löytää käyttämällä ympyrää, jonka halkaisija on yksi. Tämän ympyrän kehä on π.  

Historia

Matemaatikot ovat tienneet piin jo tuhansia vuosia, koska he ovat työskennelleet ympyröiden parissa yhtä kauan. Niinkin vanhat sivilisaatiot kuin babylonialaiset ovat kyenneet arvioimaan piitä moniin lukuihin, kuten murtolukuun 25/8 ja 256/81. Useimmat historioitsijat uskovat, että muinaisilla egyptiläisillä ei ollut käsitystä π:stä ja että vastaavuus on sattumaa.

Ensimmäinen kirjallinen maininta piistä on vuodelta 1900 eaa. Noin 1650 eaa. egyptiläinen Ahmes antoi arvon Rhindin papyruksessa. Babylonialaiset saivat selville, että piin arvo oli hieman suurempi kuin 3, tekemällä suuren ympyrän, kiinnittämällä köydenpätkän ympyrän kehälle ja halkaisijalle, kirjaamalla ylös niiden etäisyydet ja jakamalla sitten ympyrän kehä halkaisijalla.

Tieto luvusta pi siirtyi takaisin Eurooppaan ja heprealaisille, jotka tekivät luvusta tärkeän Raamatun Vanhaksi testamentiksi kutsutussa osassa. Tämän jälkeen yleisin tapa yrittää löytää pi oli piirtää monisivuinen muoto minkä tahansa ympyrän sisälle ja käyttää muodon pinta-alaa pi:n löytämiseksi. Esimerkiksi kreikkalainen filosofi Arkhimedes käytti 96-sivuista monikulmion muotoa löytääkseen pi:n arvon, mutta kiinalaiset vuonna 500 jKr. pystyivät käyttämään 16 384-sivuista monikulmiota pi:n arvon löytämiseen. Kreikkalaiset, kuten Anaxagoras Klazomenalainen, olivat myös kiireisiä selvittämään muita ympyrän ominaisuuksia, kuten sitä, miten ympyrän neliöt saadaan muodostettua ja miten luku pi saadaan neliöön. Sittemmin monet ihmiset ovat yrittäneet löytää yhä tarkempia piiarvoja.

Pi:n historia
Filosofi	Päivämäärä	Lähestymistapa
Claudius Ptolemaios	noin 150 jKr.	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	noin 800 jKr.	3.1416
al-Kashi	noin vuonna 1430	3.14159265358979
Viète	1540-1603	3.141592654
Roomen	1561-1615	3.14159265358979323
Van Ceulen	noin 1600	3.14159265358979323846264338327950288

1500-luvulla tuli käyttöön yhä parempia tapoja löytää pii, kuten ranskalainen lakimies François Vièten kehittämä monimutkainen kaava. Kreikkalaista symbolia π käytettiin ensimmäisen kerran William Jonesin vuonna 1706 kirjoittamassa esseessä.

Matemaatikko nimeltä Lambert osoitti vuonna 1761 myös, että luku pi oli irrationaalinen, eli sitä ei voi kirjoittaa murtoluvuksi tavanomaisten standardien mukaan. Toinen matemaatikko nimeltä Lindeman pystyi myös osoittamaan vuonna 1882, että pi kuului transsendentaaliluvuiksi kutsuttujen lukujen ryhmään, jotka ovat lukuja, jotka eivät voi olla polynomiyhtälön ratkaisu.

Pi:tä voidaan käyttää myös monien muiden asioiden kuin ympyröiden laskemiseen. Piin ominaisuuksien ansiosta sitä on voitu käyttää monilla muillakin matematiikan aloilla kuin geometriassa eli muotojen tutkimisessa. Tällaisia alueita ovat esimerkiksi kompleksianalyysi, trigonometria ja sarjat.

 

Pi tosielämässä

On olemassa erilaisia tapoja laskea monta π:n numeroa. Tästä on kuitenkin vain rajoitetusti hyötyä.

Pi:tä voidaan joskus käyttää minkä tahansa ympyrän pinta-alan tai ympärysmitan laskemiseen. Ympyrän ympärysmitta saadaan kaavalla C (ympärysmitta) = π × (halkaisija). Ympyrän pinta-ala saadaan kaavalla π (säde²). Tämä kaava kirjoitetaan joskus muotoon A = π r 2 {\displaystyle A=\pi r^{2}} , jossa r on minkä tahansa ympyrän säteen muuttuja ja A on kyseisen ympyrän pinta-alan muuttuja.

Ympyrän kehän laskeminen 1 mm:n virheellä:

• 30 metrin säteelle tarvitaan 4 numeroa.
• 10 numeroa, kun säde on yhtä suuri kuin maapallon säde.
• 15 numeroa säteen ollessa yhtä suuri kuin etäisyys maasta aurinkoon.
• 20 numeroa säteen ollessa yhtä suuri kuin etäisyys maasta Polarikseen.

Maaliskuun 14. päivää juhlitaan yleensä pii-päivänä, koska 14. maaliskuuta kirjoitetaan myös 3/14, joka edustaa kolmea ensimmäistä numeroa 3,14 piin approksimaatiossa. Piin päivä alkoi vuonna 2001.

 

Aiheeseen liittyvät sivut

• Numeroluettelo
• Irrationaaliset luvut
• Neliöjuuri 2:sta
• Kultainen suhde
• E (matemaattinen vakio)
• Ympyrän neliöinti
• Transsendenttiluku