Eksponenttifunktio — määritelmä ja muoto exp(x)=e^x

Eksponenttifunktio exp(x)=e^x — selkeä määritelmä, Eulerin luku e, ominaisuudet ja esimerkit. Ymmärrä kasvu, derivaatta ja sovellukset nopeasti.

Tekijä: Leandro Alegsa

Matematiikassa eksponenttifunktio on erityinen funktio, joka kasvaa yhä nopeammin muuttujan kasvaessa. Sen perusmuoto kirjoitetaan yleensä joko exp(x) tai ex, eli exp(x)=ex. {\displaystyle \exp(x)=e^{x}} Tässä e on Eulerin vakio, irrationaaliluku, jonka arvo on noin 2,71828.

Määritelmä ja perusominaisuudet

Funktio exp(x)=ex määritellään tavallisesti kaikilla reaaliluvuilla x. Tärkeitä perusominaisuuksia:

  • Alkuehto: exp(0) = 1.
  • Summaominaisuus: exp(x + y) = exp(x) · exp(y) eli ex+y = ex ey.
  • Positiivisuus: exp(x) > 0 kaikilla reaalisilla x, joten funktio ottaa kaikki positiiviset reaaliluvut arvokseen.
  • Yksikäsitteisyys: exp(x) on yksi-yhteen ja siten käännettävissä, ja sen käänteisfunktio on luonnollinen logaritmi ln(x).
  • Kasvu: exp(x) kasvaa nopeammin kuin mikä tahansa polynomi, ts. raja lim_{x→∞} ex/xn = ∞ kaikille n.

Analyyttinen esitys ja raja-arvot

Eksponenttifunktion voi määritellä ja tutkia usealla eri tavalla, jotka kaikki johtavat samaan funktioon:

  • Potenssisarja: exp(x) = \n summa_{n=0}^∞ xn/n!, eli 1 + x + x2/2! + x3/3! + ... . Tämä sarja konvergoi kaikkialla reaaliluvuilla (ja kompleksiluvuilla) ja tekee funktion analyyttiseksi.
  • Limit-määritelmä: e = lim_{n→∞} (1 + 1/n)n, ja yleisemmin exp(x) = lim_{n→∞} (1 + x/n)n (tietyin rajoituksin normaali tulkinta antaa ex).
  • Differentiaaliyhtälö: exp(x) on ainoa jatkuvasti derivoituva funktio, joka toteuttaa f'(x) = f(x) ja f(0) = 1.

Derivaatta, integraali ja käänteisfunktio

  • Derivaatta: d/dx (ex) = ex. Eksponenttifunktio on siis oman derivaatansa lähde.
  • Integraali: ∫ ex dx = ex + C.
  • Käänteisfunktio: exp on bijektio R → (0, ∞) ja sen käänteisfunktio on luonnollinen logaritmi ln(x), joka määrittelee ln(y) siten, että eln(y) = y kaikille y > 0.

Laajennus kompleksiluvuille ja Eulerin kaava

Eksponenttifunktio laajentuu luonnollisesti kompleksiluvuille: exp(z) = ez kaikille z ∈ C säilyttäen sarjamuodon. Tämän yhteydessä tärkeä identiteetti on Eulerin kaava:

eiθ = cos θ + i sin θ, mikä yhdistää eksponenttifunktion trigonometriaan ja johtaa mm. muotoon eiπ + 1 = 0.

Sovelluksia

Eksponenttifunktiolla on lukuisia sovelluksia luonnontieteissä, tekniikassa ja taloustieteissä:

  • Diskonttaus ja jatkuva korko: alkuperäinen pääoma kasvaa jatkuvasti korolla r muodossa ert.
  • Differential equations: monet lineaariset differentiaaliyhtälöt ratkaistaan eksponenttifunktioiden avulla (esim. populaation kasvu, radioaktiivinen hajoaminen).
  • Tilastotiede ja todennäköisyys: eksponenttijakauma, normaalijakauman tiheysfunktiossa e-x²/2-termi ja monissa stokastisissa malleissa.
  • Signaalinkäsittely ja fysiikka: Fourier-analyysi käyttää kompleksisia eksponentteja perusanalyysissä.

Yhteenveto

Eksponenttifunktio exp(x)=ex on perustavanlaatuinen ja hyvin käyttäytyvä funktio: se on analyyttinen, sen derivaatta on sama kuin funktio itse, se on positiivinen ja nopeasti kasvava sekä sillä on laaja-alaisia sovelluksia matematiikassa ja luonnontieteissä. Sen ominaisuudet tekevät siitä keskeisen työkalun sekä teoreettisessa että soveltavassa matematiikassa.

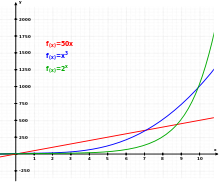
Kolme eri toimintoa: Lineaarinen (punainen), kuutiomainen (sininen) ja eksponentiaalinen (vihreä).  Zoom
Kolme eri toimintoa: Lineaarinen (punainen), kuutiomainen (sininen) ja eksponentiaalinen (vihreä).  

Ominaisuudet

Koska eksponenttifunktiot käyttävät eksponenttia, ne noudattavat samoja eksponenttisääntöjä. Näin ollen,

e x + y = exp ( x + y ) = exp ( x ) exp ( y ) = e x e y {\displaystyle e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}}} {\displaystyle e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}}.

Tästä seuraa sääntö, että x a ⋅ x b = x a + b {\displaystyle x^{a}\cdot x^{b}=x^{a+b}}} {\displaystyle x^{a}\cdot x^{b}=x^{a+b}}.

Luonnollinen logaritmi on eksponenttifunktion käänteisoperaatio, jossa:

ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}} {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}

Eksponenttifunktiolla on mielenkiintoinen ja tärkeä ominaisuus differentiaalilaskennassa:

d d x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}}

Tämä tarkoittaa, että eksponenttifunktion kaltevuus on itse eksponenttifunktio, ja sen kaltevuus on 1 kohdassa x = 0 {\displaystyle x=0}{\displaystyle x=0} . Näiden ominaisuuksien vuoksi se on tärkeä funktio matematiikassa.



 

Sovellukset

Yleinen eksponenttifunktio, jonka perusta ei välttämättä ole e {\displaystyle e} {\displaystyle e}on yksi hyödyllisimmistä matemaattisista funktioista. Sitä käytetään kuvaamaan eksponentiaalista kasvua, jota käytetään lähes kaikilla tieteenaloilla ja joka on merkittävä myös rahoituksessa. Toinen eksponenttifunktion sovellus on eksponentiaalinen hajoaminen, jota esiintyy radioaktiivisessa hajoamisessa ja valon absorptiossa.

Yksi esimerkki eksponenttifunktiosta todellisessa elämässä on pankin korko. Jos henkilö tallettaa 100 puntaa tilille, jolle maksetaan 3 % korkoa kuukaudessa, saldo on joka kuukausi (olettaen, että rahat ovat koskemattomia) seuraava:

Kuukausi

Balance

Kuukausi

Balance

Tammikuu

£100.00

Heinäkuu

£119.41

Helmikuu

£103.00

Elokuu

£122.99

Maaliskuu

£106.09

Syyskuu

£126.68

Huhtikuu

£109.27

Lokakuu

£130.48

Toukokuu

£112.55

Marraskuu

£134.39

Kesäkuu

£115.93

Joulukuu

£138.42

Huomaa, miten koroista saatava lisäraha kasvaa kuukausittain, sillä mitä suurempi alkuperäinen saldo on, sitä enemmän korkoa henkilö saa.

Seuraavassa on kaksi matemaattista esimerkkiä eksponenttifunktioista (joiden emäs on a).

a=2

x {\displaystyle x} x

Tulos

-2

0.25

-1

0.5

0

1

1

2

2

4

3

8

4

16

a=3

x {\displaystyle x} x

Tulos

-2

1/ 9

-1

1/ 3

0

1

1

3

2

9

3

27

4

81


 

Suhde matemaattiseen vakioon e

Vaikka perusluku ( a {\displaystyle a}a ) voi olla mikä tahansa nollaa suurempi luku, esimerkiksi 10 tai 1/2, usein se on erityinen luku nimeltä e. Lukua e ei voi kirjoittaa tarkasti, mutta se on lähes yhtä suuri kuin 2,71828.

Luku e on tärkeä jokaisessa eksponenttifunktiossa. Esimerkiksi pankki maksaa korkoa 0,01 prosenttia joka päivä. Yksi henkilö ottaa korkorahansa ja laittaa ne laatikkoon. 10 000 päivän (noin 30 vuoden) kuluttua hänellä on kaksi kertaa niin paljon rahaa kuin hänellä oli aluksi. Toinen henkilö ottaa korkorahansa ja laittaa ne takaisin pankkiin. Koska pankki maksaa hänelle nyt korkoa korolleen, rahamäärä on eksponenttifunktio.

Itse asiassa 10 000 päivän jälkeen hänellä ei ole 2 kertaa niin paljon rahaa kuin hän aloitti, vaan 2,718145 kertaa niin paljon rahaa kuin hän aloitti. Tämä luku on hyvin lähellä lukua e. Jos pankki maksaa korkoa useammin, jolloin joka kerta maksettava määrä on pienempi, luku on lähempänä lukua e. Jos pankki maksaa korkoa useammin, luku on pienempi.

Kuvasta voi myös nähdä, miksi luku e on tärkeä eksponenttifunktioissa. Kuvassa on kolme erilaista käyrää. Käyrä, jossa on mustat pisteet, on eksponenttifunktio, jonka perusta on hieman pienempi kuin e. Käyrä, jossa on lyhyet mustat viivat, on eksponenttifunktio, jonka perusta on hieman suurempi kuin e. Sininen käyrä on eksponenttifunktio, jonka perusta on täsmälleen sama kuin e. Punainen viiva on sinisen käyrän tangentti. Se koskettaa sinistä käyrää yhdessä kohdassa ylittämättä sitä. Henkilö voi nähdä, että punainen käyrä ylittää x-akselin, viivan, joka kulkee vasemmalta oikealle -1. Tämä pätee vain siniselle käyrälle. Tämä on syy siihen, että eksponenttifunktio, jonka perusta on e, on erityinen.



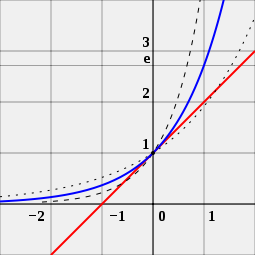
 e on ainoa sellainen luku a, että eksponenttifunktion f (x) = ax (sininen käyrä) derivaatan arvo pisteessä x = 0 on täsmälleen 1. Vertailun vuoksi on esitetty funktiot 2x (katkoviiva) ja 4x (katkoviiva), jotka eivät ole tangentteja kaltevuudeltaan 1 (punainen) olevaan suoraan.  Zoom
e on ainoa sellainen luku a, että eksponenttifunktion f (x) = ax (sininen käyrä) derivaatan arvo pisteessä x = 0 on täsmälleen 1. Vertailun vuoksi on esitetty funktiot 2x (katkoviiva) ja 4x (katkoviiva), jotka eivät ole tangentteja kaltevuudeltaan 1 (punainen) olevaan suoraan.  

Aiheeseen liittyvät sivut



 

Kysymyksiä ja vastauksia

K: Mikä on eksponenttifunktio?


V: Eksponenttifunktio on matemaattinen funktio, joka kasvaa yhä nopeammin.

K: Miten eksponenttifunktio ilmaistaan matemaattisesti?


V: Eksponenttifunktio ilmaistaan matemaattisesti muodossa exp(x) = e^x, jossa e on Eulerin vakio.

K: Mitä Eulerin vakio tarkoittaa?


V: Eulerin vakio edustaa irrationaalilukua, joka on noin 2,71828.

K: Onko eksponenttifunktio aina kasvava?


V: Kyllä, eksponenttifunktion arvo kasvaa aina x:n kasvaessa.

K: Onko olemassa jokin raja sille, kuinka nopeasti eksponenttifunktio voi kasvaa?


V: Ei, ei ole mitään rajaa sille, kuinka nopeasti eksponenttifunktio voi kasvaa, koska se jatkaa kasvuaan x:n suuremmilla arvoilla.

K: Miten voimme laskea Eulerin vakion?


V: Voimme laskea Eulerin vakion käyttämällä numeerisia menetelmiä, kuten Taylorin sarjaa tai jatkettuja murtolukuja.

K: Mitä muita sovelluksia eksponenttifunktiolla on matematiikan lisäksi?


V: Eksponenttifunktiolla on monia sovelluksia matematiikan ulkopuolella, kuten fysiikassa, kemiassa, biologiassa, taloustieteessä ja tekniikassa.


Etsiä
AlegsaOnline.com - 2020 / 2025 - License CC3