AlegsaOnline.com

Differentiaalilaskenta — määritelmä, derivaatta ja muutoksen nopeus

Differentiaalilaskenta: selkeä opas derivaattaan, muutosnopeuden laskemiseen ja käytännön sovelluksiin. Ymmärrä Newtonin ja Leibnizin periaatteet helposti.

Tekijä: Leandro Alegsa

14-12-2025

Differentiaalilaskennassa, joka on laskennan osa-alue, tutkitaan muuttujan muutosnopeutta toiseen muuttujaan nähden funktioiden avulla. Se on tapa selvittää, miten jokin muoto muuttuu pisteestä toiseen ilman, että muotoa tarvitsee jakaa äärettömään määrään osia. Differentiaalilaskenta on integraalilaskennan vastakohta. Sen kehittivät 1670- ja 1680-luvuilla Sir Isaac Newton ja Gottfried Leibniz.

Derivaatta — määritelmä

Derivaatta kuvaa, kuinka nopeasti funktion arvo muuttuu funktion argumentin muuttuessa. Formaalisti funktion f derivaatta kohdassa x on raja-arvo

f'(x) = lim_{h → 0} (f(x + h) − f(x)) / h,

kun tämä raja-arvo olemassa on. Tämä määritelmä kertoo, että derivaatta on muutosnopeus pienellä skaalalla; derivoitava funktio on silloin sanottu derivoituvaksi kyseisessä pisteessä.

Notaatio ja tulkinnat

Yleisimpiä merkintöjä: f'(x), df/dx, Df(x).
Geometrinen tulkinta: f'(x) on käyrän y = f(x) tangentin kulmakerroin pisteessä x (eli käyrän paikallinen jyrkkyys).
Fysikaalinen tulkinta: sijainnin funktion derivaatta ajan suhteen antaa nopeuden; toisen derivaatan avulla saadaan kiihtyvyys.

Säännöt, jotka helpottavat derivoimista

Seuraavat säännöt pätevät, kun funktiot ovat derivoituvia:

Summa- ja erotussääntö: (f+g)' = f' + g', (f−g)' = f' − g'.
Vakion kerroin: (c·f)' = c·f'.
Produktisääntö: (fg)' = f'g + fg'.
Osamääräsääntö: (f/g)' = (f'g − fg') / g^2, kun g ≠ 0.
Ketjusääntö: jos h(x) = f(g(x)), niin h'(x) = f'(g(x))·g'(x).

Yleisimmät derivaatat ja esimerkkejä

Tehosääntö: (x^n)' = n x^{n−1} (n on reaali, erityisesti kokonaisluvuille).
Eksponentti- ja logaritmifunktiot: (e^x)' = e^x, (a^x)' = a^x ln a, (ln x)' = 1/x (x>0).
Trigonometriset funktiot: (sin x)' = cos x, (cos x)' = −sin x, (tan x)' = sec^2 x = 1/cos^2 x.

Esimerkki: f(x) = x^2 + 3x → f'(x) = 2x + 3. Ketjusääntöesimerkki: h(x) = (sin x)^2 = u^2, u = sin x → h'(x) = 2 sin x · cos x.

Korkeammat derivaatat ja sovellukset

Voimme derivoida funktiota useamman kerran. Toista derivaattaa merkitään f''(x) tai d^2f/dx^2. Esimerkiksi fysiikassa paikka s(t):n ensimmäinen derivaatta antaa nopeuden v(t) = s'(t) ja toinen derivaatta kiihtyvyyden a(t) = s''(t).

Differentiaalilaskentaa käytetään laajasti optimoinnissa (maksimit ja minimit), fysikaalisissa malleissa, talousmatematiikassa marginaalilaskelmissa sekä differentiaaliyhtälöiden ratkaisemisessa, jotka kuvaavat monia luonnon ja tekniikan ilmiöitä.

Differentiabiliteetti ja jatkuvuus

Derivaatan olemassaolo pisteessä x vaatii, että funktio on kohdassa x jatkuva. Käänteisesti jatkuvuus ei kuitenkaan takaa derivoituvuutta: esimerkiksi |x| on jatkuva kaikkialla mutta ei derivoituva x = 0 kohdassa (vasemman ja oikean kulmakertoimet eroavat).

Kriittiset pisteet ja analyysi

Pisteet, joissa f'(x) = 0 tai f' ei ole määritelty, ovat tärkeitä, koska niissä funktio voi saavuttaa paikallisen maksimin, minimin tai kääntyä. Toisen derivaatan testi ja muut analyysimenetelmät auttavat päätelmien tekemisessä.

Vinkkejä laskemiseen

Yhdistä perussäännöt: hajota monimutkainen funktio summaan tai kertolaskuun, käytä ketjusääntöä ulkofunktion derivoimiseen.
Tarkista määrittelyalueet (esim. ln x vaatii x>0, osamäärässä jakaja ei saa olla 0).
Harjoittele perusesimerkeillä: potenssit, trigonometria, eksponenttifunktiot ja niiden yhdistelmät.

Differentiaalilaskennan peruskäsitteet antavat työkalut ymmärtää paikallista muutosta monissa käytännön ongelmissa ja muodostavat pohjan laajemmalle analyysille, kuten integraalilaskennan ja differentiaaliyhtälöiden opiskelulle.

Tausta

Toisin kuin luku, kuten 5 tai 200, muuttuja voi muuttaa arvoaan. Esimerkiksi etäisyys ja aika ovat muuttujia. Olympialaisten juoksukilpailussa henkilön etäisyys lähtöviivalta kasvaa, kun hän juoksee. Samaan aikaan sekuntikello tai kello mittaa aikaa, kun se kasvaa. Voimme mitata juoksijan keskinopeuden, jos jaamme hänen kulkemansa matkan siihen kuluneella ajalla. Tämä ei kuitenkaan kerro, millä nopeudella henkilö juoksi tasan 1,5 sekunnin kuluttua juoksusta. Jos meillä olisi etäisyys 1 sekunnin kohdalla ja etäisyys 2 sekunnin kohdalla, saisimme edelleen vain keskiarvon, vaikka se olisi luultavasti oikeampi kuin koko juoksun keskiarvo.

Ennen kuin laskutoimitus keksittiin, ainoa tapa selvittää tämä oli leikata aika yhä pienempiin palasiin, jolloin pienemmän ajan keskinopeus tulisi yhä lähemmäksi todellista nopeutta tasan 1,5 sekunnissa. Tämä oli hyvin pitkä ja vaikea prosessi, ja se piti tehdä joka kerta, kun ihmiset halusivat selvittää jotain. Kuljettajan on varmasti paljon vaikeampaa selvittää auton nopeus käyttämällä vain matkamittaria ja kelloa ilman nopeusmittaria.

Hyvin samankaltainen ongelma on löytää kaltevuus (kuinka jyrkkä se on) missä tahansa käyrän pisteessä. Suoran kaltevuus on helppo laskea - se on yksinkertaisesti se, kuinka paljon se nousee (y tai pystysuora) jaettuna sen poikkisuuntaisella osuudella (x tai vaakasuora). Jos suora on x-akselin suuntainen, sen kaltevuus on nolla. Jos suora kulkee pisteiden (x,y) = (2,10) ja (4,18) kautta, suora nousee 8 ja ylittää 2, joten sen kaltevuus on 8 jaettuna 2:lla eli 4.

Käyrällä kaltevuus on kuitenkin muuttuja (eri pisteissä on eri arvot), koska viiva taipuu. Mutta jos käyrä leikattaisiin hyvin, hyvin pieniksi paloiksi, pisteen käyrä näyttäisi lähes hyvin lyhyeltä suoralta. Sen kaltevuuden laskemiseksi voidaan siis piirtää pisteen läpi suora, jonka kaltevuus on sama kuin käyrän kaltevuus kyseisessä pisteessä. Jos se tehdään täsmälleen oikein, suoralla on sama kaltevuus kuin käyrällä, ja sitä kutsutaan tangentiksi. Mutta ei ole mitään keinoa tietää (ilman laskutoimituksia), onko tangentti täsmälleen oikea, eivätkä silmämme ole tarpeeksi tarkat, jotta voisimme olla varmoja, onko se tarkka vai vain hyvin lähellä.

Newton ja Leibniz löysivät keinon laskea kaltevuus (tai nopeus etäisyysesimerkissä) tarkasti yksinkertaisten ja loogisten sääntöjen avulla. He jakoivat käyrän äärettömään määrään hyvin pieniä paloja. Sitten he valitsivat pisteitä kiinnostavan pisteen kummaltakin puolelta ja laskivat tangentit kussakin pisteessä. Kun pisteet siirtyivät lähemmäs toisiaan kohti heitä kiinnostavaa pistettä, kaltevuus lähestyi tiettyä arvoa, kun tangentit lähestyivät käyrän todellista kaltevuutta. He sanoivat, että tämä tietty arvo, jota se lähestyi, oli todellinen kaltevuus.

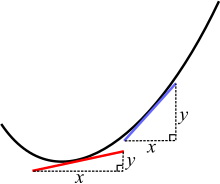
Käyrällä kahdella eri pisteellä on eri kaltevuus. Punainen ja sininen viiva ovat käyrän tangentteja.

Miten se toimii

Sanotaan, että meillä on funktio y = f(x). f on lyhenne sanoista function, joten tämä yhtälö tarkoittaa "y on funktio x:stä". Tämä kertoo meille, että se, kuinka korkealla y on pystyakselilla, riippuu siitä, mikä x (vaaka-akseli) on sillä hetkellä. Esimerkiksi yhtälöstä y = x² tiedämme, että jos x on 1, niin y on 1; jos x on 3, niin y on 9; jos x on 20, niin y on 400.

Valitse käyrästä piste A ja kutsu sen vaakasuoraa sijaintia x. Valitse sitten käyrästä toinen piste B, joka on hieman kauempana kuin piste A, ja kutsu sen vaakasuoraa sijaintia x + h. Sillä ei ole merkitystä, kuinka paljon h on; se on hyvin pieni luku.

Kun siis siirrymme pisteestä A pisteeseen B, pystysuora asema on muuttunut f(x):stä f(x + h):ksi ja vaakasuora asema on muuttunut x:stä x + h:ksi. Muista, että kaltevuus on se, kuinka paljon se nousee jaettuna sen poikkisuuntaisella osuudella. Kaltevuus on siis:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}}}} ${\frac {f(x+h)-f(x)}{h}}$

Jos viet B:n yhä lähemmäs A:ta - mikä tarkoittaa, että h tulee yhä lähemmäs 0:ta - pääsemme lähemmäs tietoa siitä, mikä on kaltevuus pisteessä A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Palataan nyt takaisin y = x²:een. Tämän kaltevuus voidaan määrittää seuraavasti:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Sovelletaan binomiteoriaa, jonka mukaan ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y+{2}}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ , voimme pelkistää lausekkeen muotoon:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\&=\lim _{h\rightarrow 0}2x+h\\\&={\frac {}{}}2x\end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Tiedämme siis ilman, että meidän tarvitsee piirtää mitään tangenttisuoraa, että missä tahansa käyrän f(x) = x² pisteessä derivaatta f'(x) (merkitty apostrofilla) on 2x missä tahansa pisteessä. Tätä prosessia, jossa kaltevuus lasketaan raja-arvojen avulla, kutsutaan differentioinniksi tai derivaatan löytämiseksi.

Leibniz päätyi samaan tulokseen, mutta kutsui h:ta nimellä "dx", joka tarkoittaa "pieni määrä x:ää". Hän kutsui f(x):n tuloksena syntyvää muutosta nimellä "dy", joka tarkoittaa "pientä määrää y:tä". Leibnizin merkintätapaa käytetään useammassa kirjassa, koska se on helppo ymmärtää, kun yhtälöistä tulee monimutkaisempia. Leibnizin notaatiossa:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

Kuva, joka osoittaa, mitä x ja x + h tarkoittavat käyrällä.

Säännöt

Edellä esitetyn järjestelmän avulla matemaatikot ovat laatineet säännöt, jotka toimivat aina, riippumatta siitä, mitä funktiota tarkastellaan. (Huomautus: tässä u {\displaystyle u} $u$ ja v {\displaystyle v} $v$ ovat molemmat funktioita x {\displaystyle x} ).

Kunto	Toiminto	Johdannainen	Esimerkki	Johdannainen
Numero itsessään	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
Suora linja	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\displaystyle y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x luvun potenssiin	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}}=ax^{a-1}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Luku kerrottuna funktiolla	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
Funktio ja toinen funktio	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\sqrt {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
Funktio miinus toinen funktio	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\sqrt {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Tuottosääntö Funktio kerrottuna toisella funktiolla	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Kvotienttisääntö Funktio jaettuna toisella funktiolla	y = u v {\displaystyle y={\frac {u}{v}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {\frac {du}{dx}}v-u{\frac {dv}{dx}}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Ketjusääntö Käytetään yhdistetyissä funktioissa	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 2 2 x - 1 = 1 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Eksponenttifunktio	y = e x {\displaystyle {\frac {}{}}y=e^{x}}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}y=e^{x}}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}e^{x}}} ${\frac {}{}}e^{x}$

Aiheeseen liittyvät sivut

Derivaatta (matematiikka)
Differentiaalioperaattori
Tavallinen differentiaaliyhtälö
Matemaattinen analyysi

Kysymyksiä ja vastauksia

K: Mitä on differentiaalilaskenta?

A: Differentiaalilaskenta on laskennan haara, jossa tutkitaan muuttujan muutosnopeutta toiseen muuttujaan verrattuna funktioiden avulla.

K: Miten se toimii?

V: Differentiaalilaskennan avulla voidaan selvittää, miten muoto muuttuu pisteestä toiseen ilman, että muotoa tarvitsee jakaa äärettömään määrään osia.

K: Kuka kehitti differentiaalilaskennan?

V: Differentiaalilaskennan kehittivät 1670- ja 1680-luvuilla Sir Isaac Newton ja Gottfried Leibniz.

K: Mitä on integraalilaskenta?

V: Integraalilaskenta on differentiaalilaskennan vastakohta. Sitä käytetään käyrän alaisten pinta-alojen ja kaarevia pintoja sisältävien kappaleiden tilavuuksien määrittämiseen.

K: Milloin differentiaalilaskenta kehitettiin?

V: Differentiaalilaskennan kehittivät 1670- ja 1680-luvuilla Sir Isaac Newton ja Gottfried Leibniz.

K: Mitä ovat differentiaalilaskennan sovellukset?

V: Joitakin differentiaalilaskennan sovelluksia ovat esimerkiksi nopeuden, kiihtyvyyden, maksimi- tai minimiarvojen, optimointiongelmien ja kaltevuuskenttien laskeminen.

K: Miksi käytämme differentiaalilaskentaa sen sijaan, että jaamme muodot äärettömään määrään paloja?

V: Käytämme sen sijaan differentiaalilaskentaa, koska sen avulla voimme selvittää, miten muoto muuttuu pisteestä toiseen ilman, että muotoa tarvitsee jakaa äärettömään määrään paloja.