Tiheysfunktio | funktio, joka luonnehtii mitä tahansa jatkuvaa todennäköisyysjakaumaa

Todennäköisyys- ja tilastotieteessä todennäköisyystiheysfunktio on funktio, joka kuvaa mitä tahansa jatkuvaa todennäköisyysjakaumaa. Satunnaismuuttujan X todennäköisyystiheysfunktio X kirjoitetaan joskus muotoon f X ( x ) {\displaystyle f_{X}(x)} $f_{X}(x)$ . Todennäköisyystiheysfunktion integraali välillä [ a , b ] {\displaystyle [a,b]} $[a,b]$ antaa todennäköisyyden, että tietty satunnaismuuttuja, jolla on tietty tiheys, sisältyy annettuun väliin. Määritelmän mukaan todennäköisyystiheysfunktio on ei-negatiivinen koko alueellaan, jolla integraali on 1.

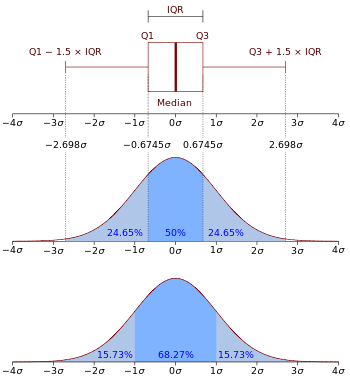
Boxplot ja normaalijakauman N(0, σ2 ) todennäköisyystiheysfunktio.

Todennäköisyystiheys vs. todennäköisyyden massafunktio

Todennäköisyyden massafunktio on diskreetille todennäköisyysjakaumalle sama kuin todennäköisyystiheysfunktio jatkuvalle todennäköisyysjakaumalle. Todennäköisyystiheysfunktio on välttämätön, jotta voidaan työskennellä jatkuvien jakaumien kanssa.

Satunnaismuuttuja, jolla on jatkuva todennäköisyysjakauma, voi saada minkä tahansa arvon kyseisen jakauman sisällä. Nopan heitto antaa luvut 1-6 todennäköisyydellä 1 6 {\displaystyle {\tfrac {1}{6}}}} ${\tfrac {1}{6}}$ , mutta tämä ei ole jatkuva funktio, koska vain luvut 1-6 ovat mahdollisia.

Sitä vastoin kaksi ihmistä ei ole samanpituisia tai -painoisia. Todennäköisyystiheysfunktion avulla voidaan määrittää todennäköisyys, jolla ihmiset ovat 180 senttimetrin ja 181 senttimetrin välillä tai 80 kilogramman ja 81 kilogramman välillä, vaikka näiden kahden rajan välillä on äärettömän monta arvoa.

Aiheeseen liittyvät sivut

Kumulatiivinen jakauman funktio

Kysymyksiä ja vastauksia

K: Mikä on todennäköisyystiheysfunktio?

A: Todennäköisyystiheysfunktio on funktio, joka luonnehtii mitä tahansa jatkuvaa todennäköisyysjakaumaa.

K: Miten satunnaismuuttujan X todennäköisyystiheysfunktio kirjoitetaan?

A: X:n todennäköisyystiheysfunktio kirjoitetaan joskus muotoon f_X(x).

K: Mitä todennäköisyystiheysfunktion integraali edustaa?

V: Todennäköisyystiheysfunktion integraali edustaa todennäköisyyttä, että tietty satunnaismuuttuja, jolla on tietty tiheys, sisältyy annettuun väliin.

Kysymys: Onko todennäköisyystiheysfunktio aina ei-negatiivinen koko alueellaan?

V: Kyllä, määritelmän mukaan todennäköisyystiheysfunktio on koko alueellaan ei-negatiivinen.

Kysymys: Saavuttaako integraatio intervalliin summa 1:n?

Vastaus: Kyllä, integrointi intervallien yli on summa 1.

K: Minkä tyyppistä jakaumaa todennäköisyystiheysfunktio kuvaa?

V: Todennäköisyystiheysfunktio kuvaa mitä tahansa jatkuvaa todennäköisyysjakaumaa.