Tilastot | soveltavan matematiikan osa-alue, joka käsittelee tietojen keräämistä, järjestämistä, analysointia, lukemista ja esittämistä

Historia

Ensimmäiset tunnetut tilastot ovat väestönlaskentatietoja. Babylonialaiset tekivät väestönlaskennan noin 3500 eaa., egyptiläiset noin 2500 eaa. ja muinaiset kiinalaiset noin 1000 eaa.

1500-luvulta lähtien matemaatikot, kuten Gerolamo Cardano, kehittivät todennäköisyysteorian, jonka ansiosta tilastotieteestä tuli tiede. Siitä lähtien ihmiset ovat keränneet ja tutkineet tilastoja monista asioista. Puut, meritähdet, tähdet, kivet, sanat, melkein kaikki, mitä voidaan laskea, on ollut tilastojen kohteena.

 

Tietojen kerääminen

Ennen kuin voimme kuvata maailmaa tilastojen avulla, meidän on kerättävä tietoja. Tilastoissa kerättäviä tietoja kutsutaan mittauksiksi. Kun olemme keränneet tietoja, käytämme yhtä tai useampaa numeroa kuvaamaan kutakin havaintoa tai mittausta. Oletetaan esimerkiksi, että haluamme selvittää, kuinka suosittu tietty tv-ohjelma on. Voimme valita katsojien kokonaispopulaatiosta ryhmän ihmisiä (jota kutsutaan otokseksi). Sitten kysymme jokaiselta otokseen kuuluvalta katsojalta, kuinka usein hän katsoo ohjelmaa. Otos on dataa, jonka voi nähdä, ja perusjoukko on dataa, jota ei voi nähdä (olettaen, että kaikilta perusjoukon katsojilta ei kysytä). Toisena esimerkkinä, jos haluamme tietää, voiko tietty lääke auttaa alentamaan verenpainetta, voimme antaa lääkettä ihmisille jonkin aikaa ja mitata heidän verenpaineensa ennen ja jälkeen.

 

Kuvailevat ja päättelytilastot

Näkyviä tietoja kuvaavia lukuja kutsutaan kuvaileviksi tilastoiksi. Lukuja, jotka tekevät ennusteita tiedoista, joita ei voi nähdä, kutsutaan päättelytilastoiksi.

Kuvailevissa tilastoissa käytetään numeroita kuvaamaan tietojen ominaisuuksia. Esimerkiksi naisten keskipituus Yhdysvalloissa on kuvaileva tilasto: se kuvaa perusjoukon (naisten pituus Yhdysvalloissa) ominaisuutta (keskipituus).

Kun tulokset on tiivistetty ja kuvattu, niitä voidaan käyttää ennustamiseen. Tätä kutsutaan päättelytilastoksi. Esimerkiksi eläimen koko riippuu monista tekijöistä. Osaa näistä tekijöistä säätelee ympäristö, mutta osa on periytyvää. Biologi voi siis laatia mallin, jonka mukaan jälkeläiset ovat suurella todennäköisyydellä pieniä - jos vanhemmat ovat olleet pieniä. Tämän mallin avulla kokoa voidaan todennäköisesti ennustaa paremmin kuin vain arvaamalla satunnaisesti. Testaamalla, voidaanko tietyllä lääkkeellä parantaa tiettyä tilaa tai sairautta, verrataan yleensä lääkettä saavien ihmisten tuloksia lumelääkettä saavien ihmisten tuloksiin.

 

Menetelmät

Useimmiten keräämme tilastotietoja tekemällä kyselyitä tai kokeita. Esimerkiksi mielipidekysely on eräänlainen kyselytutkimus. Valitsemme pienen joukon ihmisiä ja kysymme heiltä kysymyksiä. Sitten käytämme heidän vastauksiaan aineistona.

On tärkeää valita, mitkä henkilöt otetaan mukaan tutkimukseen tai tiedonkeruuseen, sillä se vaikuttaa suoraan tilastoihin. Kun tilastot on tehty, ei voida enää määrittää, mitkä henkilöt otetaan. Oletetaan, että haluamme mitata suuren järven vedenlaatua. Jos otamme näytteet jätevesiviemärin vierestä, saamme erilaiset tulokset kuin jos näytteet otetaan kaukaisesta ja vaikeasti saavutettavasta kohdasta järveä.

Näytteitä otettaessa esiintyy yleisesti kahdenlaisia ongelmia:

1. Jos otoksia on paljon, otokset ovat todennäköisesti hyvin lähellä sitä, mitä ne ovat todellisessa populaatiossa. Jos näytteitä on kuitenkin hyvin vähän, ne saattavat poiketa hyvin paljon siitä, mitä ne ovat todellisessa populaatiossa. Tätä virhettä kutsutaan satunnaisvirheeksi (ks. myös Virheet ja jäännökset tilastoissa).
2. Näytteenottajat on valittava huolellisesti. Yleensä heidät valitaan satunnaisesti. Jos näin ei tehdä, otokset saattavat poiketa hyvin paljon siitä, mitä ne todellisuudessa ovat koko populaatiossa. Tämä pätee, vaikka näytteitä otettaisiin suuri määrä. Tällaista virhettä kutsutaan harhaksi.

Virheet

Voimme vähentää satunnaisvirheitä ottamalla suuremman otoksen, ja voimme välttää jonkin verran harhaa valitsemalla satunnaisesti. Joskus suuria satunnaisotoksia on kuitenkin vaikea ottaa. Lisäksi harhaa voi syntyä, jos eri ihmisiltä ei kysytä kysymyksiä tai jos he kieltäytyvät vastaamasta kysymyksiin tai jos he tietävät saavansa valehoitoa. Näitä ongelmia voi olla vaikea korjata. Katso lisätietoja kohdasta keskivirhe.

 

Kuvailevat tilastot

Tietojen keskikohdan löytäminen

Aineiston keskiarvoa kutsutaan keskiarvoksi. Keskiarvo kertoo tyypillisestä yksilöstä populaatiossa. Usein käytetään kolmenlaisia keskiarvoja: keskiarvo, mediaani ja moodi.

Alla olevissa esimerkeissä käytetään näitä esimerkkitietoja:

Nimi	A	B	C	D	E	F	G	H	I	J
Pisteet	23	26	49	49	57	64	66	78	82	92

Keskiarvo

Keskiarvon kaava on

x ¯ = 1 N ∑ i = 1 N x i = x 1 + x 2 + ⋯ + x N N {\displaystyle {\bar {\x}}={\frac {1}{N}}\sum _{i=1}^{N}x_{i}={\frac {x_{1}+x_{2}+\cdots +x_{N}}{N}}}}

Jossa x 1 , x 2 , ... , x N {\displaystyle x_{1},x_{2},\ldots ,x_{N}}} ovat aineisto ja N {\displaystyle N} on populaation koko (ks. myös Sigma-merkintä).

Tämä tarkoittaa, että keskiarvo lasketaan laskemalla kaikki arvot yhteen ja jakamalla se sitten arvojen lukumäärällä. Yllä olevassa esimerkissä keskiarvo on:

x ¯ = ( 23 + 26 + 49 + 49 + 57 + 64 + 66 + 78 + 82 + 92 ) / 10 = 58.6 {\displaystyle {\bar {x}}=(23+26+49+49+57+64+66+78+82+92)/10=58.6}}

Keskiarvon ongelma on, että se ei kerro mitään siitä, miten arvot jakautuvat. Hyvin suuret tai hyvin pienet arvot muuttavat keskiarvoa paljon. Tilastoissa nämä ääriarvot saattavat olla mittausvirheitä, mutta joskus perusjoukko todella sisältää näitä arvoja. Esimerkiksi jos huoneessa on 10 ihmistä, jotka ansaitsevat 10 dollaria päivässä, ja yksi, joka ansaitsee 1 000 000 dollaria päivässä. Aineiston keskiarvo on 90 918 dollaria päivässä. Vaikka se on keskiarvo, keskiarvo ei tässä tapauksessa ole yksittäisen henkilön ansaitsema summa, eikä se siten ole kovin hyödyllinen joihinkin tarkoituksiin.

Edellä kuvattu keskiarvo on "aritmeettinen keskiarvo". Muuntyyppiset keskiarvot ovat hyödyllisiä joihinkin tarkoituksiin.

Mediaani

Mediaani on aineiston keskimmäinen arvo. Tietylle aineistolle X {\displaystyle X} tämä kirjoitetaan joskus muotoon X ~ {\displaystyle {\widetilde {X}}} . Mediaanin löytämiseksi lajittelemme tiedot pienimmästä luvusta suurimpaan ja valitsemme sitten keskimmäisen luvun. Jos dataa on parillinen määrä, aivan keskellä ei ole numeroa, joten valitsemme kaksi keskimmäistä ja laskemme niiden keskiarvon. Yllä olevassa esimerkissä on 10 tietoa, kaksi keskimmäistä on "57" ja "64", joten mediaani on (57+64)/2 = 60,5.

Toisena esimerkkinä, kuten keskiarvon tuloesimerkin yhteydessä, ajatellaan huonetta, jossa on 10 ihmistä, joiden tulot ovat 10, 20, 20, 20, 40, 50, 60, 90, 90, 90, 100 ja 1 000 000 dollaria. Tässä tapauksessa mediaani on 55 dollaria, koska 55 dollaria on kahden keskimmäisen luvun, 50 ja 60 dollarin, keskiarvo. Jos ääriarvo 1 000 000 dollaria jätetään huomiotta, keskiarvo on 53 dollaria. Tässä tapauksessa mediaani on lähellä arvoa, joka saadaan, kun ääriarvo jätetään pois. Mediaani ratkaisee ääriarvojen ongelman, kuten edellä keskiarvon määritelmässä kuvattiin.

Tila

Tila on yleisimmin esiintyvä tieto. Esimerkiksi englannin kielen yleisin kirjain on e-kirjain. Sanoisimme, että "e" on kirjainten jakauman moodi.

Toisena esimerkkinä, jos huoneessa on 10 ihmistä, joiden tulot ovat 10, 20, 20, 20, 40, 50, 60, 60, 90, 90, 90, 90, 100 ja 1 000 000 dollaria, moodi on 90 dollaria, koska 90 dollaria esiintyy kolme kertaa ja kaikki muut arvot esiintyvät harvemmin kuin kolme kertaa.

Tiloja voi olla useampia kuin yksi. Jos huoneessa on esimerkiksi 10 henkilöä, joiden tulot ovat 10, 20, 20, 20, 20, 50, 60, 90, 90, 90, 100 ja 1 000 000 dollaria, moodit ovat 20 ja 90 dollaria. Tämä on bimodaalinen eli siinä on kaksi moodia. Bimodaalisuus on hyvin yleistä, ja se osoittaa usein, että tiedot ovat kahden eri ryhmän yhdistelmä. Esimerkiksi kaikkien aikuisten keskipituus Yhdysvalloissa on bimodaalinen jakauma. Tämä johtuu siitä, että miehillä ja naisilla on erilliset keskipituudet, jotka ovat miehillä 1,763 m (5 ft 9 + 1⁄2 in) ja naisilla 1,622 m (5 ft 4 in). Nämä huiput näkyvät, kun molemmat ryhmät yhdistetään.

Moodi on ainoa keskiarvon muoto, jota voidaan käyttää sellaisten tietojen osalta, joita ei voida asettaa järjestykseen.

Tietojen hajonnan määrittäminen

Toinen asia, jonka voimme sanoa datajoukosta, on se, kuinka hajallaan se on. Yleinen tapa kuvata aineiston hajontaa on keskihajonta. Jos aineiston keskihajonta on pieni, suurin osa aineistosta on hyvin lähellä keskiarvoa. Jos taas keskihajonta on suuri, suuri osa aineistosta poikkeaa hyvin paljon keskiarvosta.

Otoksen keskihajonta on yleensä erilainen kuin sen perusjoukon keskihajonta . Tämän vuoksi kirjoitamme σ {\displaystyle \sigma } populaation keskihajonnalle ja s {\displaystyle s} otoksen keskihajonnalle.

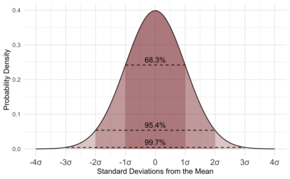
Jos tiedot noudattavat yleistä mallia, jota kutsutaan normaalijakaumaksi, on erittäin hyödyllistä tietää keskihajonta. Jos tiedot noudattavat tätä kaavaa (sanoisimme, että tiedot ovat normaalijakautuneita), noin 68 sadasta tiedosta poikkeaa keskiarvosta vähemmän kuin keskihajonta. Sen lisäksi noin 95 joka sadasta mittaustuloksesta poikkeaa keskiarvosta alle kaksi kertaa keskihajonnan verran, ja noin 997 mittaustulosta 1000:sta on lähempänä keskiarvoa alle kolme keskihajontaa.

Muut kuvailevat tilastot

Voimme käyttää tilastoja myös selvittääksemme, että tietty prosenttiosuus, prosenttipiste, määrä tai murto-osa ihmisistä tai asioista ryhmässä tekee jotakin tai kuuluu tiettyyn luokkaan.

Esimerkiksi yhteiskuntatieteilijät ovat tilastojen avulla saaneet selville, että 49 prosenttia maailman ihmisistä on miehiä.

 

Aiheeseen liittyvät ohjelmistot

Tilastotieteilijöiden tueksi on kehitetty monia tilasto-ohjelmia:

• MATLAB
• R
• SAS Institute
• SPSS (IBM:n tekemä)