Pythagoraan lause – määritelmä, kaava ja esimerkit

Tutustu Pythagoraan lauseeseen: selkeä määritelmä, helposti ymmärrettävä kaava ja käytännön esimerkit suorakulmaisen kolmion hypotenuusan laskuun.

Tekijä: Leandro Alegsa

20-12-2025 14:39

Matematiikassa Pythagoraan lause tai Pythagoraan lause on lausuma suorakulmaisen kolmion sivuista.

Yksi suorakulmaisen kolmion kulmista on aina 90 astetta. Tämä kulma on oikea kulma. Suorakulman vieressä olevia kahta sivua kutsutaan jaloiksi ja toista sivua hypotenuusaksi. Hypotenuusa on suoran kulman vastakkainen sivu, ja se on aina pisin sivu.

Määritelmä ja kaava

Pythagoraan lause sanoo, että suorakulmaisessa kolmiossa, jossa jalkojen pituudet ovat a ja b ja hypotenuusan pituus c, pätee

a² + b² = c²

Tämä on perusmuotoinen ja yleisesti käytetty muotoilu, jossa a ja b ovat oikean kulman viereiset sivut ja c on niiden vastakkainen sivu.

Esimerkkejä

Esimerkki 1 — hypotenuusan laskeminen: Kolmion jalat ovat 3 m ja 4 m. Hypotenuusa c saadaan laskemalla
c = √(3² + 4²) = √(9 + 16) = √25 = 5 m.
Esimerkki 2 — jalan laskeminen: Hypotenuusa on 13 cm ja toinen jalka on 5 cm. Toinen jalka b on
b = √(13² − 5²) = √(169 − 25) = √144 = 12 cm.
Pythagoraan triplettit: Kokonaislukuratkaisuja, joissa a, b, c ovat kokonaislukuja, kutsutaan tripleteiksi. Tunnettuja esimerkkejä ovat (3,4,5), (5,12,13) ja (8,15,17). Näissä kaikissa pätee a² + b² = c².

Lyhyt todistus

On olemassa monia todistuksia Pythagoraan lauseelle. Yksi helppo tapa on käyttää samanlaisuutta:

Piirrä suorakulmainen kolmio ja vedä korkeus hypotenuusasta särmään. Tämä jakaa kolmion kahdeksi pienemmäksi suorakulmaiseksi kolmioksi, jotka ovat samanlaisia alkuperäisen kanssa. Tästä näkee suhdeyhtälöt, joista yhteenvetona saadaan a² + b² = c².

Toinen tunnettu geometrinen todistus on järjestää neljä yhtenevää suorakulmaista kolmiota neliön sisälle ja verrata muodostuvien alueiden summia. Molemmat lähestymistavat johtavat samaan algebraiseen yhtälöön.

Käänteinen lause

Pythagoraan lauseen käänteinen muoto on myös tärkeä: jos kolmion sivuilla a, b, c pätee a² + b² = c², niin kolmiolla on suora kulma sivujen a ja b välissä. Toisin sanoen kaava antaa sekä ehdon että riittävän ehdon kolmion suorakulmaisuudelle.

Sovelluksia ja lisätietoa

Koordinaattigeometria: Pythagoraan lause johtaa etäisyyskaavaan tason pisteiden välillä: etäisyys pisteistä (x1,y1) ja (x2,y2) on √((x2−x1)² + (y2−y1)²).
Rakentaminen ja mittaus: Lause on käytännöllinen oikean kulman tarkistamiseen ja etäisyyksien laskemiseen rakentamisessa ja kartoituksessa.
Trigonometrian perusta: Useat trigonometriset kaavat ja suhteet perustuvat Pythagoraan lauseeseen, esimerkiksi sin²θ + cos²θ = 1, joka on sama periaate yksikköympyrässä.
Yleistäminen: Pythagoraan lauseen periaatetta voidaan laajentaa koordinaatistoon (kuten edellä) ja kolmiulotteiseen avaruuteen: pisteiden etäisyys (x1,y1,z1) ja (x2,y2,z2) välillä on √((Δx)² + (Δy)² + (Δz)²).

Huomioita laskuissa

Muista käyttää samoja yksiköitä kaikissa sivuissa ennen laskemista. Jos tulos on neliöjuuri, usein pyöristetään sopivalle desimaalitasolle käytännön tarpeen mukaan. Kokonaislukutriplettien tunnistaminen voi helpottaa laskuja ilman neliöjuuria.

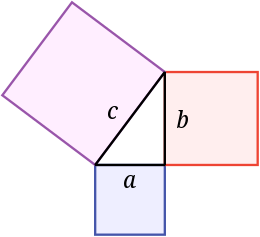
Pythagoraan lause Jalkojen (a ja b) kahden neliön pinta-alojen summa on yhtä suuri kuin hypotenuusan (c) neliön pinta-ala.

Teorian väite

Pythagoraan lauseen mukaan hypotenuusan neliön pinta-ala on yhtä suuri kuin jalkojen neliöiden pinta-alojen summa. Tässä kuvassa sinisen neliön pinta-ala lisättynä punaisen neliön pinta-alaan muodostaa violetin neliön pinta-alan. Se on nimetty kreikkalaisen matemaatikon Pythagoraan mukaan:

Jos jalkojen pituudet ovat a ja b ja hypotenuusan pituus on c, niin a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Todistustyypit

Tästä lauseesta on olemassa monia erilaisia todistuksia. Ne jakautuvat neljään luokkaan:

Lineaarisiin suhteisiin perustuvat: algebralliset todisteet.
Pinta-alojen vertailuun perustuvat: geometriset todistukset.
Ne, jotka perustuvat vektorioperaatioon.
Massaan ja nopeuteen perustuvat: dynaamiset todistukset.

Todiste

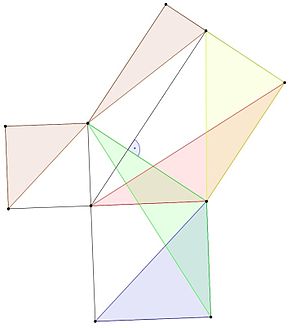
Kreikkalainen matemaatikko Eudoxus Cnidusilainen löysi yhden todistuksen Pythagoraan lauseesta.

Todistuksessa käytetään kolmea lemmaa:

Kolmioilla, joilla on sama pohja ja korkeus, on sama pinta-ala.
Kolmio, jonka pohja ja korkeus ovat yhtä suuret kuin neliön sivu, on pinta-alaltaan yhtä suuri kuin neliön puolikas.
Kolmioilla, joiden kaksi sivua ja yksi kulma ovat yhtenevät, on sama pinta-ala.

Todiste on:

Sinisellä kolmiolla on sama pinta-ala kuin vihreällä kolmiolla, koska sillä on sama pohja ja korkeus (lemma 1).
Vihreällä ja punaisella kolmiolla on molemmilla kaksi sivua, jotka ovat yhtä suuret kuin saman neliön sivut, ja kulma, joka on yhtä suuri kuin suora kulma (90 asteen kulma) ja kolmion kulma, joten ne ovat yhteneviä ja niillä on sama pinta-ala (lemma 3).
Punaisten ja keltaisten kolmioiden pinta-alat ovat yhtä suuret, koska niiden korkeudet ja pohjat ovat samat (lemma 1).
Sinisen kolmion pinta-ala on yhtä suuri kuin keltaisen kolmion pinta-ala, koska

A b l u e = A g r e e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Ruskeilla kolmioilla on sama pinta-ala samoista syistä.
Sinisellä ja ruskealla on kummallakin puolet pienemmän neliön pinta-alasta. Niiden pinta-alojen summa on puolet suuremman neliön pinta-alasta. Tästä johtuen pienten neliöiden pinta-alojen puolikkaat ovat yhtä suuria kuin puolet isomman neliön pinta-alasta, joten niiden pinta-ala on sama kuin isomman neliön pinta-ala.

Todistus samankaltaisten kolmioiden avulla

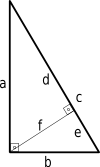
Pythagoraan lauseelle saadaan toinen todiste käyttämällä samankaltaisia kolmioita.

d a = a c ⇒ a 2 = d c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad {a^{2}}={dc}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad {a^{2}}={dc}\quad (1)$

e b = b c ⇒ b 2 = e c ( 2 ) {\displaystyle {\frac {e}{b}}={\frac {b}{c}}\quad \Rightarrow \quad {b^{2}}={ec}\quad (2)} ${\frac {e}{b}}={\frac {b}{c}}\quad \Rightarrow \quad {b^{2}}={ec}\quad (2)$

Lisää kuvasta yhtälöt (1) ja (2):

a 2 + b 2 = d c + e c ⇒ a 2 + b 2 = c ( d + e ) ⇒

${a^{2}}+{b^{2}}={dc+ec}\quad \Rightarrow a^{2}+b^{2}=c(d+e)\quad \Rightarrow a^{2}+b^{2}=c(c)$

Ja saamme:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!.} $c^{2}=a^{2}+b^{2}\,\!.$

Pythagoraan kolmikot

Pythagoraan kolmoset ovat kolme kokonaislukua, jotka sopivat yhtälöön a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Kolmio, jonka sivut ovat 3, 4 ja 5, on tunnettu esimerkki. Jos a=3 ja b=4, niin 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}} $3^{2}+4^{2}=5^{2}$ koska 9 + 16 = 25 {\displaystyle 9+16=25}} $9+16=25$ . Tämä voidaan esittää myös muodossa 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.} {\displaystyle {\sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Kolme-neljä-viisi-kolmio toimii kaikille 3:n, 4:n ja 5:n kertaluvuille. Toisin sanoen myös luvut 6, 8, 10 tai 30, 40 ja 50 ovat Pythagoraan kolmioita. Toinen esimerkki kolmikosta on kolmio 12-5-13, koska 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13}} . ${\sqrt {12^{2}+5^{2}}}=13$

Pythagoraan kolmikkoa, joka ei ole muiden kolmikkojen monikerta, kutsutaan primitiiviseksi pythagoraaniseksi kolmikoksi. Mikä tahansa primitiivinen Pythagoraan kolmio voidaan löytää lausekkeella ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , mutta seuraavien ehtojen on täytyttävä. Ne asettavat rajoituksia arvoille m {\displaystyle m} ja n {\displaystyle n} .

m {\displaystyle m} ja n {\displaystyle n} ovat positiivisia kokonaislukuja.
m {\displaystyle m} ja n {\displaystyle n} ei ole muita yhteisiä tekijöitä kuin 1.
m {\displaystyle m} ja n {\displaystyle n} ovat vastakkaisen pariteetin omaavia. m {\displaystyle m} ja n {\displaystyle n} ovat vastakkaisen pariteetin omaavia, kun m {\displaystyle m} on parillinen ja n {\displaystyle n} on pariton tai m {\displaystyle m} on pariton ja n {\displaystyle n} on parillinen.
m > n {\displaystyle m>n} $m>n$ .

Jos kaikki neljä ehtoa täyttyvät, arvot m {\displaystyle m} ja n {\displaystyle n} muodostavat primitiivisen Pythagoraan kolmikon.

m = 2 {\displaystyle m=2} $m=2$ ja n = 1 {\displaystyle n=1} $n=1$ muodostavat alkeellisen Pythagoraan kolmikon. Arvot täyttävät kaikki neljä ehtoa. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ ja m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , joten syntyy kolmikko ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} . $(3,4,5)$

Kysymyksiä ja vastauksia

Q: Mikä on Pythagoraan lause?

A: Pythagoraan lause on lausuma suorakulmaisen kolmion sivuista.

K: Mikä kulma on aina 90 astetta suorakulmaisessa kolmiossa?

V: Yksi suorakulmaisen kolmion kulmista on aina yhtä suuri kuin 90 astetta, ja sitä kutsutaan suorakulmaksi.

K: Millä nimellä kutsutaan oikokulman vieressä olevia kahta sivua?

V: Oikean kulman vieressä olevia kahta sivua kutsutaan jaloiksi.

K: Miksi kutsutaan suoran kulman vastakkaista sivua?

V: Suorakulman vastakkaista sivua kutsutaan hypotenuusaksi, ja se on aina pisin sivu.

K: Onko tämän lauseen laskemiseen olemassa yhtälö?

V: Kyllä, tämän lauseen laskemiseen on olemassa yhtälö, jonka mukaan "hypotenuusan pituuden neliö on yhtä suuri kuin kahden muun sivun pituuksien neliöiden summa".

K: Ovatko kaikki kolmiot, joissa on 90 asteen kulmat, "oikeita" kolmioita?

V: Ei, kaikkia 90 asteen kulmia sisältäviä kolmioita ei pidetä "oikeina" kolmioina; vain ne, joissa yksi sivu (hypotenuusa) on pidempi kuin kaksi muuta sivua ja muodostaa 90 asteen kulman päähänsä, voidaan luokitella "oikeiksi" kolmioiksi.

Etsiä