Keskihajonta – määritelmä, laskukaavat ja esimerkit
Selkeä opas keskihajontaan: määritelmä, laskukaavat (populaatio & otos), tulkinta ja käytännön esimerkit. Ymmärrä σ ja s nopeasti ja käytännössä.
Keskihajonta on luku, jota käytetään kertomaan, miten ryhmän mittaustulokset poikkeavat keskiarvosta (keskiarvosta tai odotusarvosta). Pieni keskihajonta tarkoittaa, että useimmat luvut ovat lähellä keskiarvoa, kun taas suuri keskihajonta tarkoittaa, että luvut ovat enemmän hajallaan.
Ilmoitettu virhemarginaali on yleensä kaksi kertaa keskihajonta. Tutkijat ilmoittavat yleisesti kokeissa esiintyvien lukujen keskihajonnan keskimääräisestä luvusta. He päättävät usein, että vain kaksi- tai kolminkertaista keskihajontaa suuremmat erot ovat tärkeitä. Keskihajonta on käyttökelpoinen myös rahassa, jossa korkotulojen keskihajonta osoittaa, kuinka paljon yhden henkilön korkotulot voivat poiketa keskiarvosta.
Usein voidaan mitata vain näyte tai osa ryhmästä. Tällöin voidaan löytää koko ryhmän keskihajontaa lähellä oleva luku hieman erilaisella yhtälöllä, jota kutsutaan otoksen keskihajonnaksi ja joka selitetään jäljempänä. Tällöin koko ryhmän keskihajonta esitetään kreikkalaisella kirjaimella 
Keskihajonnan laskukaavat
Koko populaation keskihajonta (σ) lasketaan kaavalla
σ = sqrt( (1/N) Σ_{i=1}^N (x_i − μ)^2 )
missä N on populaation koko, x_i ovat havaintoja ja μ on populaation keskiarvo.
Otoksen (näytteen) keskihajonta (s) lasketaan tyypillisesti kaavalla, joka sisältää Besselin korjauksen:
s = sqrt( (1/(n−1)) Σ_{i=1}^n (x_i − x̄)^2 )
missä n on otoskoko, x̄ on otoksen keskiarvo. Jakaminen (n−1):llä korjaa otosvarianssin ala- tai yliarviointia ja antaa paremman arvion populaation varianssista.
Esimerkki laskusta
Data: 2, 4, 4, 4, 5, 5, 7, 9 (n = 8)
1) Laske keskiarvo: x̄ = (2+4+4+4+5+5+7+9)/8 = 40/8 = 5
2) Erotukset ja neliöt: (2−5)^2=9, (4−5)^2=1, …, (9−5)^2=16. Näiden neliöiden summa = 32.
3) Populaation varianssi (jos nämä olisivat koko populaatio): σ^2 = 32/8 = 4 → σ = 2.
4) Otoksen varianssi (jos kyseessä on näyte populaatiosta): s^2 = 32/(8−1) ≈ 4,571 → s ≈ 2,14.
Tulkinta ja käytännön huomioita
- Yksikkö: Keskihajonta on samassa yksikössä kuin alkuperäiset havainnot (esim. senttimetreissä, euroissa).
- Pieni vs. suuri: Pieni keskihajonta kertoo, että arvot ovat kohtuullisen lähellä keskiarvoa. Suuri keskihajonta kertoo suurista vaihteluista.
- Herkkyys ääripäille: Keskihajonta reagoi voimakkaasti poikkeaviin arvoihin (outliereihin). Jos data sisältää paljon ääripäitä, keskihajonta voi antaa harhaanjohtavan kuvan hajonnasta—tällöin vaihtoehtoja ovat mm. mediaaniin perustuva keskipoikkeama (MAD) tai kvartiiliväli (IQR).
- Suhde varianssiin: Varianssi on keskihajonnan neliö (σ^2 tai s^2). Varianssia käytetään monissa matemaattisissa johtopäätöksissä, mutta se on eri yksikössä kuin alkuperäinen muuttuja.
- Normaaliarvon sääntö: Jos data on likimain normaalijakautunutta, noin 68 % arvoista on yhden keskihajonnan sisällä, 95 % kahden ja 99,7 % kolmen sisällä (ns. 68–95–99,7-sääntö).
- Virhemarginaali ja keskivirhe: Monet tekstit mainitsevat, että virhemarginaali on "noin kaksi kertaa" jokin arvo. On tärkeää erottaa keskihajonta ja keskivirhe (standard error). Keskivirhe (SE) on otoksen keskihajonta jaettuna juurella otoskoosta: SE = s / sqrt(n). Luottamusvälin leveys (virhemarginaali) perustuu yleensä SE:ään (esim. noin 2·SE ~ 95 % luottamusväli normaalijakaumalle), ei suoraan yksittäiseen havaintojen keskihajontaan.
Käyttökohteet
Keskihajontaa käytetään lähes kaikissa tilastollisissa analyyseissä: kuvailevassa tilastotieteessä vaihtelun mittarina, hypoteesitestauksessa, regressioanalyysissä ja riskin mittaamisessa rahoituksessa (esim. tuottojen volatiliteetti).
Yhteenveto
Keskihajonta on keskeinen mittari, joka kertoo kuinka paljon havaintosi yleensä poikkeavat keskiarvosta. Muista erottaa populaation ja otoksen laskukaavat, huomioida outlierien vaikutus ja käyttää keskivirhettä, kun arvioit keskiarvon tarkkuutta ja lasket virhemarginaaleja.
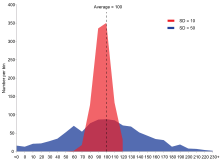
Esimerkki kahdesta otospopulaatiosta, joilla on sama keskiarvo ja erilaiset keskihajonnat. Punaisen populaation keskiarvo on 100 ja SD 10; sinisen populaation keskiarvo on 100 ja SD 50.
.png)
Normaalijakauman (tai kellokäyrän) kuvaaja. Kunkin värillisen kaistan leveys on yksi keskihajonta.
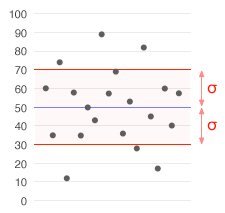
Aineisto, jonka keskiarvo on 50 (sinisellä) ja keskihajonta (σ) 20.
Perusesimerkki
Tarkastellaan ryhmää, jossa on seuraavat kahdeksan numeroa:
Näiden kahdeksan luvun keskiarvo on 5:
Jos haluat laskea populaation keskihajonnan, etsi ensin kunkin luettelossa olevan luvun ero keskiarvoon. Neliöi sitten kunkin erotuksen tulos:
Seuraavaksi etsitään näiden arvojen keskiarvo (summa jaettuna lukujen lukumäärällä). Viimeiseksi otetaan neliöjuuri:
Vastaus on populaation keskihajonta. Kaava pitää paikkansa vain, jos ne kahdeksan lukua, joista aloitimme, ovat koko ryhmä. Jos ne ovat vain osa satunnaisesti poimitusta ryhmästä, voimme saada puolueettoman arvion siitä, mikä on populaation keskihajonta, jakamalla yllä olevan kaavan alareunassa (nimittäjässä) luvulla 7 (joka on n - 1) eikä luvulla 8 (joka on n). Tällöin vastaus on (harhakorjattu) otoksen keskihajonta. Tätä kutsutaan Besselin korjaukseksi. Käytämme usein tätä korjausta, koska otosvarianssi eli otoksen keskihajonnan neliö on perusjoukon varianssin harhaton estimaattori, toisin sanoen otosvarianssin odotusarvo tai pitkän aikavälin keskiarvo on yhtä suuri kuin perusjoukon (todellinen) varianssi. Vaikka Besselin korjaus on varianssin puolueeton estimaatti, tällä estimaatilla on suurempi keskimääräinen neliövirhe kuin vinoutuneella estimaatilla eli vinoutunut estimaatti (eli jakamalla n:llä eikä n-1:llä) on keskimäärin lähempänä todellista arvoa.
Lisää esimerkkejä
Tässä on hieman vaikeampi esimerkki todellisesta elämästä: Yhdysvalloissa aikuisten miesten keskipituus on 70", ja keskihajonta on 3". Kolmen tuuman keskihajonta tarkoittaa, että useimpien miesten (noin 68 %, jos oletetaan normaalijakauma) pituus on 3 tuumaa korkeampi tai 3 tuumaa lyhyempi kuin keskiarvo (67-73 tuumaa) - yksi keskihajonta. Lähes kaikkien miesten (noin 95 %) pituus on 6" pitempi tai 6" lyhyempi kuin keskimäärin (64"-76") - kaksi keskihajontaa. Kolme keskihajontaa sisältää kaikki luvut 99,7 prosentille tutkittavasta otospopulaatiosta. Tämä pätee, jos jakauma on normaali (kellonmuotoinen).
Jos keskihajonta olisi nolla, kaikki miehet olisivat täsmälleen 70" pitkiä. Jos keskihajonta olisi 20", jotkut miehet olisivat paljon pidempiä tai paljon lyhyempiä kuin keskimäärin, tyypillinen vaihteluväli olisi noin 50"-90".
Toinen esimerkki: Jokaisen kolmen ryhmän {0, 0, 14, 14}, {0, 6, 8, 14} ja {6, 6, 8, 8, 8} keskiarvo on 7. Niiden keskihajonnat ovat 7, 5 ja 1. Kolmannen ryhmän keskihajonta on paljon pienempi kuin kahdella muulla ryhmällä, koska sen luvut ovat kaikki lähellä 7:ää. Yleisesti ottaen keskihajonta kertoo, kuinka kaukana keskiarvosta loput luvuista ovat, ja sen yksikköinä käytetään samoja yksiköitä kuin itse luvuilla. Jos esimerkiksi ryhmä {0, 6, 8, 14} on neljän veljeksen ryhmän ikä vuosina, keskiarvo on 7 vuotta ja keskihajonta 5 vuotta.
Keskihajonta voi toimia epävarmuuden mittarina. Esimerkiksi tieteessä toistuvien mittausten ryhmän keskihajonta auttaa tutkijoita tietämään, kuinka varmoja he ovat keskimääräisestä luvusta. Kun päätetään, ovatko kokeesta saadut mittaukset sopusoinnussa ennusteen kanssa, näiden mittausten keskihajonta on erittäin tärkeä. Jos kokeista saatu keskiluku on liian kaukana ennustetusta luvusta (etäisyys mitataan keskihajontana), testattava teoria ei ehkä pidä paikkaansa. Lisätietoja on kohdassa ennustusväli.
Sovellusesimerkkejä
Arvojen keskihajonnan ymmärtäminen antaa meille mahdollisuuden tietää, kuinka suuri ero "keskiarvoon" (keskiarvoon) on odotettavissa.
Sää
Yksinkertainen esimerkki: tarkastellaan kahden kaupungin, toisen sisämaan ja toisen valtameren läheisyydessä sijaitsevan kaupungin, keskimääräisiä päivittäisiä korkeimpia lämpötiloja. On hyödyllistä ymmärtää, että valtameren läheisyydessä sijaitsevien kaupunkien päivittäisten korkeiden lämpötilojen vaihteluväli on pienempi kuin sisämaassa sijaitsevien kaupunkien. Näissä kahdessa kaupungissa voi kummassakin olla sama keskimääräinen vuorokauden korkein lämpötila. Rannikkokaupungin päivittäisen korkean lämpötilan keskihajonta on kuitenkin pienempi kuin sisämaakaupungin.
Urheilu
Toinen tapa nähdä asia on tarkastella urheilujoukkueita. Missä tahansa urheilulajissa on joukkueita, jotka ovat hyviä joissakin asioissa ja toisissa taas eivät. Korkeimmalle sijoittuneissa joukkueissa ei ole suuria eroja kyvyissä. Ne menestyvät hyvin useimmissa luokissa. Mitä pienempi niiden kykyjen keskihajonta kussakin kategoriassa on, sitä tasapainoisempia ja johdonmukaisempia ne ovat. Joukkueet, joilla on suurempi keskihajonta, ovat kuitenkin vähemmän ennustettavia. Joukkueella, joka on yleensä huono useimmissa luokissa, on pieni keskihajonta. Joukkueella, joka on yleensä hyvä useimmissa luokissa, on myös alhainen keskihajonta. Joukkue, jolla on suuri keskihajonta, saattaa kuitenkin olla sellainen joukkue, joka tekee paljon pisteitä (vahva hyökkäys) mutta antaa toisen joukkueen tehdä paljon pisteitä (heikko puolustus).
Kun yritetään tietää etukäteen, mitkä joukkueet voittavat, voidaan tarkastella eri joukkueiden "tilastojen" keskihajontoja. Odotetusta poikkeavat luvut voivat verrata vahvuuksia ja heikkouksia ja osoittaa, mitkä syyt voivat olla tärkeimpiä, kun tiedetään, mikä joukkue voittaa.
Kilpaurheilussa mitataan aika, joka kuljettajalta kuluu jokaisen kierroksen ajamiseen radan ympäri. Kuljettaja, jonka kierrosaikojen keskihajonta on pieni, on tasaisempi kuin kuljettaja, jonka keskihajonta on suurempi. Tätä tietoa voidaan käyttää apuna ymmärtämään, miten kuljettaja voi lyhentää kierroksen loppuun kuluvaa aikaa.
Raha
Rahassa keskihajonta voi tarkoittaa riskiä siitä, että hinta nousee tai laskee (osakkeet, joukkovelkakirjat, kiinteistöt jne.). Se voi tarkoittaa myös riskiä siitä, että ryhmä hintoja nousee tai laskee (aktiivisesti hallinnoidut sijoitusrahastot, indeksirahastot tai ETF:t). Riski on yksi syy tehdä päätöksiä siitä, mitä ostaa. Riski on luku, jonka avulla ihmiset voivat tietää, kuinka paljon rahaa he voivat ansaita tai menettää. Kun riski kasvaa, sijoituksen tuotto voi olla odotettua suurempi ("plus" keskihajonta). Sijoitus voi kuitenkin myös menettää odotettua enemmän rahaa (miinus keskihajonta).
Esimerkiksi henkilön oli valittava kahden osakkeen välillä. Osakkeen A keskimääräinen tuotto viimeisten 20 vuoden aikana on ollut 10 prosenttia ja keskihajonta 20 prosenttiyksikköä (pp). Osakkeen B keskimääräinen tuotto viimeisten 20 vuoden aikana oli 12 prosenttia, mutta keskihajonta oli suurempi, 30 prosenttiyksikköä. Riskiä ajatellen henkilö saattaa päättää, että osake A on turvallisempi valinta. Vaikka hän ei ehkä tienaa yhtä paljon rahaa, hän ei todennäköisesti myöskään menetä paljon rahaa. Henkilö saattaa ajatella, että osake B:n 2 prosenttiyksikköä korkeampi keskiarvo ei ole 10 prosenttiyksikön ylimääräisen keskihajonnan (suurempi riski tai epävarmuus odotetusta tuotosta) arvoinen.
Normaalisti jakautuneita lukuja koskevat säännöt
Useimmissa standardipoikkeamaa koskevissa yhtälöissä oletetaan, että luvut ovat normaalisti jakautuneita. Tämä tarkoittaa, että luvut ovat jakautuneet tietyllä tavalla keskiarvon molemmin puolin. Normaalijakaumaa kutsutaan myös Gaussin jakaumaksi, koska sen löysi Carl Friedrich Gauss. Sitä kutsutaan usein kellokäyräksi, koska luvut jakautuvat siten, että ne muodostavat kellon muodon kuvaajassa.
Luvut eivät ole normaalijakautuneita, jos ne ryhmittyvät keskiarvon toiselle tai kolmannelle puolelle. Luvut voivat olla hajallaan ja silti normaalisti jakautuneita. Keskihajonta kertoo, kuinka laajalle luvut ovat levinneet.

Tummansininen on alle yhden keskihajonnan päässä keskiarvosta. Normaalijakauman osalta tämä sisältää 68,27 prosenttia luvuista, kun taas kahden keskihajonnan (keski- ja tummansininen) osuus on 95,45 prosenttia, kolmen keskihajonnan (vaalea, keski- ja tummansininen) osuus on 99,73 prosenttia ja neljän keskihajonnan osuus on 99,994 prosenttia.
Keskiarvon ja keskihajonnan välinen suhde.
Tietojoukon keskiarvo (keskiarvo) ja keskihajonta kirjoitetaan yleensä yhteen. Tällöin henkilö voi ymmärtää, mikä on keskimääräinen luku ja kuinka laajalle muut ryhmän luvut ovat hajallaan.
Lukujoukon jakaantumista voidaan kuvata myös variaatiokertoimella (CV), joka on keskihajonta jaettuna keskiarvolla. Se on dimensioton luku. Variaatiokerroin kerrotaan usein 100 prosentilla ja kirjoitetaan prosentteina.
Historia
Karl Pearson käytti termiä keskihajonta ensimmäisen kerran kirjallisesti vuonna 1894, kun hän oli käyttänyt sitä luennoillaan. Se korvasi aiemmat nimitykset samasta ajatuksesta: esimerkiksi Gauss käytti keskivirhettä.
Aiheeseen liittyvät sivut
- Tarkkuus ja täsmällisyys
- Näytteen koko
- Vakiovirhe
- Poikkeama
Kysymyksiä ja vastauksia
K: Mikä on keskihajonta?
V: Keskihajonta on luku, jota käytetään kertomaan, miten ryhmän mittaukset poikkeavat keskiarvosta (keskiarvosta tai odotusarvosta).
K: Mitä tarkoittaa pieni keskihajonta?
A: Pieni keskihajonta tarkoittaa, että suurin osa luvuista on lähellä keskiarvoa.
K: Mitä tarkoittaa suuri keskihajonta?
V: Suuri keskihajonta tarkoittaa, että luvut ovat enemmän hajallaan.
K: Miten keskihajontaa käytetään rahassa?
V: Rahassa korkotulojen keskihajonta osoittaa, kuinka paljon yhden henkilön korkotulot saattavat poiketa keskiarvosta.
K: Milloin voidaan mitata vain osaa ryhmästä?
V: Monesti voidaan mitata vain otos tai osa ryhmästä.
K: Miten koko ryhmän keskihajonta esitetään?
V: Koko ryhmän keskihajonta esitetään kreikkalaisella kirjaimella َ \displaystyle \sigma }. .
K: Miten otoksen keskihajonta esitetään?
V: Otoksen keskihajontaa edustaa s {\displaystyle s} .
Etsiä




