Alkeisalgebra – määritelmä, perusteet ja esimerkit

Tutustu alkeisalgebraan: määritelmä, muuttujat, peruslait, yhtälöiden ratkaisu ja käytännön esimerkit — selkeä opas oppilaille ja opettajille.

Tekijä: Leandro Alegsa

28-01-2026 00:06

Alkeisalgebra on alkeisalgebran alkeistaso, jota oppilaille opetetaan. Se on usein yksi seuraavista matematiikan osa-alueista, joita oppilaille opetetaan aritmetiikan jälkeen. Aritmetiikassa esiintyy vain numeroita ja operaattoreita, kuten +, -, × ja ÷, kun taas algebrassa muuttujia (kuten a, x, y) käytetään numeroiden edustajina. Tämä on hyödyllistä, koska:

Sen avulla ihmiset voivat ratkaista "tuntemattomia" lukuja koskevia ongelmia. Tämä tarkoittaa yhtälöiden oppimista ja niiden ratkaisemista (esimerkiksi "etsi luku x, jossa 3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ ").
Se mahdollistaa aritmeettisten sääntöjen yleistämisen. Vaikka jotkut oppilaat ymmärtävät, että 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3} $3+4=4+3$ , se auttaa todistamaan, että a + b = b + a {\displaystyle a+b=b+a} kaikille a:lle ja b:lle. Tämän ansiosta algebra on hyvä askel abstrahoinnin oppimisessa (yleisten ideoiden oppiminen monista esimerkeistä).
Se auttaa ihmisiä ymmärtämään ja luomaan toiminnallisia suhteita (joita joskus kutsutaan myös syy-seuraussuhteiksi). Esimerkki tästä on "jos myydään x lippua, voitto on 3 x - 10 $3x-10$ dollaria".

Nämä kolme ovat alkeisalgebran keskeiset osa-alueet. Alkeisalgebraa käytetään usein monissa muissa oppiaineissa, kuten luonnontieteissä, liike-elämässä ja rakentamisessa. Abstraktia algebraa, joka on paljon edistyneempi aihe, opetetaan yleensä vasta yliopistossa.

Perusteet: muuttujat, lausekkeet ja yhtälöt

Muuttuja on kirjain (esim. x, y, a), joka edustaa tuntematonta tai muuttuvaa lukua. Lauseke on joukko numeroita, muuttujia ja operaattoreita (esim. 2x + 5). Yhtälö on lauseke, jossa on yhtäsuuruusmerkki, esimerkiksi 3x + 1 = 10; tavoitteena on usein ratkaista, mikä x on.

Tärkeitä laskusääntöjä ja ominaisuuksia

Vaihdantalaki (kommutatiivisuus) summalle ja kertolaskulle: a + b = b + a, a · b = b · a.
Liitäntälaki (assosiatiivisuus): (a + b) + c = a + (b + c), sama kertolaskulle.
Distributiivisuus: a(b + c) = ab + ac — tämä mahdollistaa sulkujen avaamisen ja lausekkeiden yksinkertaistamisen.
Yhtälön käsittely: mitä teet toiseen puoleen, sinun täytyy tehdä myös toiseen. Esim. vähennä tai jaa molemmilta puolilta.
Like termien yhdistäminen: yhdistele muuttujiltaan samankaltaiset osat, esim. 2x + 3x = 5x.

Yhtälön ratkaiseminen — esimerkki

Ratkaistaan esimerkkiyhtälö 3x + 1 = 10 (ks. yllä oleva kuva). Vaiheet:

Vähennä 1 molemmilta puolilta: 3x = 9.
Jaa 3:lla: x = 3.
Tarkista sijoittamalla takaisin alkuperäiseen: 3·3 + 1 = 10, pitää paikkansa.

Lisätekniikoita ja käsitteitä alkeisalgebrassa

Laajentaminen ja faktorisointi: avaaminen (esim. a(b + c) → ab + ac) ja sulkujen ottaminen yhteiseksi tekijäksi (esim. ab + ac → a(b + c)).
Ratkaiseminen useammalle muuttujalle: lineaarisissa yhtälöryhmissä käytetään eliminointi- tai sijoitusmenetelmää.
Epäyhtälöt: toimivat kuten yhtälöt, mutta merkitsevät suuruussuhdetta (> , < , ≥ , ≤). Muista kääntää merkki, kun kerrot tai jaat negatiivisella luvulla.
Funktiot: lauseke, joka yhdistää muuttujan toiseen arvoon, esimerkiksi f(x) = 2x + 1. Alkeisalgebrassa opitaan tavallisesti lineaaristen funktioiden perusominaisuudet.

Sovelluksia arjessa ja eri aloilla

Alkeisalgebra näkyy monessa käytännön tilanteessa: budjetin laatimisessa (tulot − kulut), rakennusmittojen laskemisessa, fysiikassa kaavojen käsittelyssä ja talouden malleissa. Se myös luo perustan ohjelmoinnille ja edistyneemmälle matematiikalle.

Vinkkejä oppimiseen

Harjoittele peruslaskusääntöjä: yhdistä samanlaiset termit, avaa sulut ja käytä distributiivisuutta.
Ratkaise monia esimerkkitehtäviä ja tarkista vastaukset sijoittamalla ne takaisin.
Käytä selkeitä vaiheita: eristä muuttuja, toimi molemmilla puolilla samalla tavalla ja kirjoita välivaiheet ylös.
Älä pelkää merkkien käsittelyä: negatiivisten lukujen kanssa toimiminen on yleinen virhelähde.

Alkeisalgebra antaa työkalut ongelmien jäsentelyyn ja loogiseen ajatteluun. Kun nämä perusasiat hallitaan hyvin, siirtyminen vaikeampiin aiheisiin, kuten abstraktiin algebraan tai reaali- ja funktioteoriaan, on helpompaa.

Yksinkertaisia algebran ongelmia

Jos yhtälössä on vain yksi tuntematon luku, se on joskus helppo ratkaista. Tuntematonta lukua kutsutaan nimellä "x":

2 x + 4 = 12. {\displaystyle 2x+4=12.\,} $2x+4=12.\,$

Ratkaistaksesi yksinkertaisen yhtälön, jossa on yksi tuntematon määrä, lisää, vähennä, kerro tai jaa yhtälön molemmat puolet samalla luvulla, jotta tuntematon määrä x saadaan yhtälön toiselle puolelle. Kun x on itsessään toisella puolella, käytä aritmetiikkaa määrittääksesi yhtälön toisella puolella olevan määrän. Esimerkiksi vähentämällä 4 molemmista sivuista yllä olevassa yhtälössä:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4-4=12-4\,} $2x+4-4=12-4\,$

saada:

2 x = 8 {\displaystyle 2x=8\,} $2x=8\,$

Jaetaan molemmat puolet 2:lla:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}}\,} ${\frac {2x}{2}}={\frac {8}{2}}\,$

saada:

x = 4. {\displaystyle x=4.\,} $x=4.\,$

Voi olla hyödyllistä ajatella tätä yhtälöä keinuvasarana tai tasapainona: mitä teet toiselle puolelle, sinun on tehtävä toiselle puolelle, ja päätavoitteesi on saada x itsestään.

Määritelmät

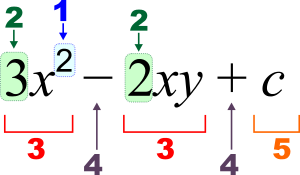
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ on seuraavat komponentit:

1 : Eksponentti (potenssi), 2 : Kerroin, 3 : termi, 4 : operaattori, 5 : vakio, x , y {\displaystyle x,y} : $x,y$ muuttujat.

Kysymyksiä ja vastauksia

K: Mitä on alkeisalgebra?

V: Alkeisalgebra on opiskelijoille opetettava algebran perusmuoto. Se seuraa yleensä aritmetiikkaa, ja siinä käytetään muuttujia (kuten a, x, y) lukujen merkitsemiseen yhtälöissä.

K: Mihin alkeisalgebraa käytetään?

V: Alkeisalgebraa voidaan käyttää tuntemattomia lukuja koskevien ongelmien ratkaisemiseen, aritmeettisten sääntöjen yleistämiseen, funktionaalisten suhteiden ymmärtämiseen ja luomiseen, ja sitä käytetään usein monissa muissa oppiaineissa, kuten luonnontieteissä, liike-elämässä ja rakentamisessa.

K: Miten alkeisalgebra auttaa ihmisiä ymmärtämään abstrakteja ideoita?

V: Alkeisalgebra auttaa ihmisiä oppimaan yleisiä ideoita monista esimerkeistä todistamalla, että a+b=b+a kaikille a:lle ja b:lle. Näin he voivat ymmärtää paremmin abstrakteja käsitteitä.

K: Onko abstrakti algebra kehittyneempää kuin alkeisalgebra?

V: Kyllä, abstraktia algebraa opetetaan yleensä korkeakoulun loppuvaiheessa, ja se on paljon edistyneempää kuin alkeisalgebra.

K: Millaisia yhtälötyyppejä alkeisalgebra sisältää?

V: Alkeisalgebraan kuuluu yhtälöitä, joissa muuttujat (kuten a, x, y) edustavat lukuja sekä operaattoreita kuten +,- ,× ja ÷ .
3x+1=10 {\displaystyle 3x+1=10}

K: Miten alkeisalgebran ymmärtäminen voi auttaa muissa oppiaineissa?

V: Alkeisalgebran ymmärtäminen voi auttaa muissa oppiaineissa, kuten luonnontieteissä, liike-elämässä tai rakennusalalla, koska sen avulla voidaan ratkaista tuntemattomia lukuja koskevia ongelmia ja luoda funktionaalisia suhteita eri muuttujien välille.

Etsiä