Algebra — määritelmä, yhtälöt, funktiot ja käytännön sovellukset

Algebra — selkeä opas: määritelmä, yhtälöt, funktiot ja käytännön sovellukset fysiikassa, tekniikassa ja arjen laskuissa.

Tekijä: Leandro Alegsa

16-11-2025 16:55

Algebra (arabian kielestä: الجبر, translitteroituna "al-jabr", tarkoittaa "rikkinäisten osien yhdistämistä") on osa matematiikkaa. Siinä käytetään muuttujia edustamaan arvoa, jota ei vielä tunneta. Kun käytetään yhtäsuuruusmerkkiä (=), sitä kutsutaan yhtälöksi. Erittäin yksinkertainen yhtälö, jossa käytetään muuttujaa, on: 2 + 3 = x {\displaystyle 2+3=x} $2+3=x$ . Tässä esimerkissä x = 5 {\displaystyle x=5} $x=5$ , tai voitaisiin myös sanoa, että " x {\displaystyle x} on yhtä kuin viisi". Tätä kutsutaan x:n ratkaisemiseksi {\displaystyle x} .

Yhtälöiden lisäksi on olemassa epätasa-arvoja (pienempi kuin ja suurempi kuin). Yhtälön erityistyyppiä kutsutaan funktioksi. Sitä käytetään usein kuvaajien tekemisessä, koska se muuttaa aina yhden syötteen yhdeksi tulosteeksi.

Algebraa voidaan käyttää todellisten ongelmien ratkaisemiseen, koska algebran säännöt toimivat todellisessa elämässä ja numeroita voidaan käyttää todellisten asioiden arvojen esittämiseen. Fysiikka, tekniikka ja tietokoneohjelmointi ovat aloja, joilla algebraa käytetään jatkuvasti. Algebraa on hyödyllistä osata myös maanmittauksessa, rakentamisessa ja liike-elämässä, erityisesti kirjanpidossa.

Algebraa harrastavat ihmiset käyttävät numeroiden sääntöjä ja matemaattisia operaatioita, joita käytetään numeroilla. Yksinkertaisimpia ovat yhteen-, vähennys-, kerto- ja jakolasku. Kehittyneemmät operaatiot sisältävät eksponentteja, alkaen neliöistä ja neliöjuurista.

Algebraa käytettiin ensin yhtälöiden ja epätasa-arvojen ratkaisemiseen. Kaksi esimerkkiä ovat lineaariset yhtälöt (suoran yhtälö, y = m x + b {\displaystyle y=mx+b} $y=mx+b$ tai y = m x + c {\displaystyle y=mx+c} $y=mx+c$ ) ja kvadraattiset yhtälöt, joiden muuttujat ovat neliöitä (kerrotaan itsellään, esim: 2 ⋅ 2 {\displaystyle 2\cdot 2} $2\cdot 2$ , 3 ⋅ 3 {\displaystyle 3\cdot 3} $3\cdot 3$ tai x ⋅ x {\displaystyle x\cdot x} $x\cdot x$ ).

Mikä on algebra käytännössä?

Algebra tarkoittaa symbolien (yleensä kirjaimien) käyttämistä lukujen ja niiden suhteiden kuvaamiseen. Symbolit tekevät mahdolliseksi yleisten kaavojen muodostamisen ja ratkaisujen etsimisen ilman, että kaikki arvot olisivat tiedossa etukäteen. Algebra kehittää loogista päättelyä ja abstraktia ajattelua: sen avulla voidaan keksiä yleispäteviä sääntöjä ja soveltaa niitä moniin tilanteisiin.

Yhtälöt ja muuttujan ratkaiseminen

Yhtälön ratkaisemisen perusajatus on eristää muuttuja (esim. x) toisilleen vastakkaisilla operaatiolla. Tätä kutsutaan käänteisoperaatioiden käytöksi: jos yhtälössä on +5, vähennetään 5; jos kerrotaan 3:lla, jaetaan 3:lla. Vaiheittainen periaate on:

Tasapainon säilyttäminen: tee sama operaatio molemmille puolille.
Käytä vastakkaisia operaatioita: lisää-vähennä, kerro-jaa.
Yhtälö yksinkertaistetaan kunnes muuttuja eristyy.

Esimerkki: ratkaise 3x + 2 = 11. Ensin vähennetään 2: 3x = 9. Sitten jaetaan 3: x = 3.

Funktiot ja kuvaajat

Funktio on sääntö, joka liittää jokaiseen syötearvoon (domain) täsmälleen yhden tulosarvon (range). Perusesimerkki on lineaarinen funktio f(x) = mx + b, jossa m on kulmakerroin (suhde syötteen ja tuloksen muutoksen välillä) ja b on vakiotermi (y-akselin leikkauspiste). Funktioita käytetään kuvaajien piirrossa: jokaista x-arvoa kohti piirretään vastaava f(x)-arvo.

Funktioiden merkityksiä ja ominaisuuksia ovat muun muassa:

Domaani: mitkä x-arvot ovat sallittuja (esim. ei nollalla jakamista).
Ydinaluet: mihin arvojoukkoon funktio kuuluvia tuloksia kuuluu.
Yhden-suoruus tai ei: onko funktio lineaarinen, polynominen, eksponentiaalinen, jne.

Epätasa-arvot

Epätasa-arvot (esim. <, >, ≤, ≥) toimivat kuten yhtälöt, mutta ne kertovat, miten kaksi lauseketta sijoittuu toisiinsa nähden. Ratkaisualue on usein väli tai yhdistelmien joukko, ei yksittäinen luku. Esimerkiksi ratkaisu x + 3 < 7 antaa kaikki x-arvot, jotka ovat pienempiä kuin 4.

Yleisimpiä yhtälötyyppejä

Lineaariset yhtälöt ovat muotoa ax + b = 0 tai y = mx + c — niiden kuvaajat ovat suoria. Ratkaiseminen tapahtuu eristämällä muuttuja.

Kvadrattiset yhtälöt ovat muotoa ax² + bx + c = 0. Niillä voi olla nolla, yksi tai kaksi reaalista ratkaisua riippuen diskriminantista D = b² − 4ac. Ratkaisut saadaan kaavalla x = (−b ± sqrt(D)) / (2a). Kvadrattiset funktiot kuvaavat paraabelia, jonka huippu ja nollakohdat ovat olennaisia ominaisuuksia.

Perussäännöt ja operaatiot

Algebrassa käytetään samoja peruslaskutoimituksia kuin aritmetiikassa: yhteenlasku, vähennyslasku, kertolasku ja jakolasku. Lisäksi usein tarvitaan:

Eksponentit (potenssit) ja juuret.
Tekijöihin jako (faktorointi) ja lausekkeiden sieventäminen.
Yhtälöparien ratkaiseminen (korvaus- ja vähennysmenetelmät).

Käytännön sovelluksia

Algebran säännöt soveltuvat moniin käytännön tilanteisiin. Konkreettisia esimerkkejä:

Fysiikassa yhtälöt kuten s = vt + ½at² kuvaavat liikkeen sijaintia ajan funktiona.
Tekniikassa mittojen ja rasitusten laskeminen vaatii usein yhtälöiden ratkaisemista ja funktioiden tutkimista.
Talous- ja liike-elämässä korkolaskut, budjetointi ja tappioiden/voittojen analysointi perustuvat algebrallisiin malleihin.
Tietokoneohjelmoinnissa algoritmit ja datan analyysi käyttävät algebraa ja funktioita.
Maanmittauksessa ja rakentamisessa algebra auttaa pituuksien, kulmien ja pinta-alojen laskennassa.

Esimerkkejä arjen tehtävistä

Kuinka käyttää algebraa arjessa:

Laske tarvittavien laattamäärä: jos huoneen pinta-ala on A ja yhden laatan ala on a, tarvittavien laattojen määrä n = A / a (pyöristetään ylöspäin).
Budjetissa: jos tulosi ovat T, kiinteät kulut K ja osuus säästettävästä S prosenttia, käytä yhtälöä T − K − S·T = käytettävissä oleva summa.
Korkolaskussa: yksinkertainen korko I = P·r·t (pääoma P, korkoprosentti r desimaalina, aika t vuosina).

Miten oppia algebraa tehokkaasti

Hyviä käytäntöjä algebran opiskeluun:

Harjoittele vaiheittain: ymmärrä perusoperaatiot ja käänteisoperaatiot hyvin.
Piirrä kuvaajia: visuaalinen esitys usein auttaa muistamaan funktioiden käyttäytymistä.
Ratkaise paljon esimerkkejä ja eri tyyppisiä tehtäviä: yhtälöitä, epätasa-arvoja ja funktioita.
Käytä apuna laskinta tai tietokoneohjelmaa, mutta harjoittele ensin käsinratkaisuja, jotta ymmärrys syvenee.
Kommentoi ja selitä oma ratkaisusi ääneen tai kirjoita se ylös — selittäminen auttaa jäsentämään ajatuksia.

Algebra on käytännöllinen ja laaja työkalu, joka yhdistää yksinkertaiset numerot monimutkaisiin malleihin. Kun perusperiaatteet ovat selvät, algebra auttaa ymmärtämään ja ratkaisemaan sekä arkisia että tieteellisiä ongelmia.

Historia

Babylonialaiset ja kreikkalaiset geometrikot, kuten Aleksandrian Hero, kehittivät algebran varhaisia muotoja. Sana "algebra" on kuitenkin latinankielinen muoto arabian kielen sanasta Al-Jabr ("valu"), ja se on peräisin matematiikan kirjasta Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Essee valun ja yhtälön laskemisesta"), jonka kirjoitti 9. vuosisadalla persialainen matemaatikko Muhammad ibn Mūsā al-Khwārizmī, joka oli Uzbekistanin Khwarizmissa syntynyt muslimi. Hän kukoisti Al-Ma'mounin alaisuudessa Bagdadissa, Irakissa vuosina 813-833 jKr. ja kuoli noin vuonna 840 jKr. Kirja tuotiin Eurooppaan ja käännettiin latinaksi 1200-luvulla. Silloin kirjalle annettiin nimi "Algebra". (Matemaatikon nimen loppuosa al-Khwarizmi muutettiin sanaksi, joka oli helpompi sanoa latinaksi, ja siitä tuli englanninkielinen sana algorithm).

Esimerkkejä

Tässä on yksinkertainen esimerkki algebran ongelmasta:

Sue:lla on 12 karkkia ja Annilla 24 karkkia. He päättävät jakaa niin, että heillä on yhtä monta karkkia. Kuinka monta karkkia kummallakin on?

Voit ratkaista ongelman seuraavilla ohjeilla:

Saadakseen saman määrän karkkeja Annin on annettava osa Sue:lle. Olkoon x {\displaystyle x} karkkien määrä, jonka Ann antaa Sue:lle.
Suen karkit lisättynä x {\displaystyle x} , on oltava samat kuin Annin karkit vähennettynä x {\displaystyle x} . Tämä kirjoitetaan seuraavasti: 12 + x = 24 - x {\displaystyle 12+x=24-x}. $12+x=24-x$
Vähennä 12 yhtälön molemmista puolista. Näin saadaan: x = 12 - x {\displaystyle x=12-x} $x=12-x$ . (Mitä tapahtuu yhtälön toisella puolella, täytyy tapahtua myös toisella puolella, jotta yhtälö olisi edelleen tosi. Kun siis tässä tapauksessa 12 vähennettiin molemmilta puolilta, syntyi keskivaihe 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} $12+x-12=24-x-12$ . Kun henkilö on oppinut tämän, keskimmäistä askelta ei kirjoiteta ylös).
Lisää x {\displaystyle x} yhtälön molemmille puolille. Näin saadaan: 2 x = 12 {\displaystyle 2x=12} $2x=12$
Jaa yhtälön molemmat puolet luvulla 2. Näin saadaan x = 6 {\displaystyle x=6} $x=6$ . Vastaus on kuusi. Tämä tarkoittaa, että jos Ann antaa Sue:lle 6 karkkia, heillä on yhtä monta karkkia.
Tarkista tämä laittamalla 6 takaisin alkuperäiseen yhtälöön, missä x {\displaystyle x} oli: 12 + 6 = 24 - 6 {\displaystyle 12+6=24-6} $12+6=24-6$
Näin saadaan 18 = 18 {\displaystyle 18=18} $18=18$ , mikä on totta. Kummallakin on nyt 18 karkkia.

Harjoittelun avulla algebraa voidaan käyttää, kun edessä on ongelma, jota on liian vaikea ratkaista muulla tavoin. Sellaiset ongelmat kuin moottoritien rakentaminen, matkapuhelimen suunnittelu tai sairauden parannuskeinon löytäminen vaativat kaikki algebraa.

Kirjoitusalgebra

Kuten useimmissa matematiikan osissa, y:n {\displaystyle y} lisääminen z:hen {\displaystyle z} $z$ (tai y {\displaystyle y} plus z {\displaystyle z} $z$ ) kirjoitetaan y + z {\displaystyle y+z} $y+z$ ;

Vähentämällä z {\displaystyle z} $z$ y {\displaystyle y} (tai y {\displaystyle y} miinus z {\displaystyle z} $z$ ) kirjoitetaan y - z {\displaystyle y-z} $y-z$ ;

ja jaetaan y {\displaystyle y} ja z {\displaystyle z} $z$ (tai y {\displaystyle y} ja z {\displaystyle z} $z$ ) kirjoitetaan muodossa y / z {\displaystyle y/z} $y/z$ tai y z {\displaystyle y \over z} ${y \over z}$ .

Algebrassa y {\displaystyle y} kertominen z {\displaystyle z} $z$ (tai y {\displaystyle y} kertaa z {\displaystyle z} $z$ ) voidaan kirjoittaa kolmella eri tavalla: y ⋅ z {\displaystyle y\cdot z} $y\cdot z$ , y ( z ) {\displaystyle y(z)} $y(z)$ tai vain y z {\displaystyle yz} $yz$ . Kaikki nämä merkinnät tarkoittavat samaa asiaa: y {\displaystyle y} kertaa z {\displaystyle z} $z$ . Symboli " × {\displaystyle \times } tarkoittaa " × \times }. $\times$ " ei käytetä algebrassa, koska se muistuttaa liikaa kirjainta x {\displaystyle x} , jota käytetään usein muuttujana.

Kun algebrassa kerromme luvun ja muuttujan, voimme yksinkertaisesti kirjoittaa luvun kirjaimen eteen: 5 ⋅ y ⟺ 5 y {\displaystyle 5\cdot y\iff 5y} $5\cdot y\iff 5y$ . Kun luku on 1, sitä ei kirjoiteta, koska 1 kertaa mikä tahansa luku on tämä luku ( 1 ⋅ y = y {\displaystyle 1\cdot y=y} $1\cdot y=y$ ), joten sitä ei tarvita. Ja kun se on 0, voimme poistaa termit kokonaan, koska 0 kertaa jokin luku on nolla ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} $0\cdot y=0$ ).

Sivuhuomautuksena, algebrassa ei tarvitse käyttää kirjaimia x {\displaystyle x} tai y {\displaystyle y} . Muuttujat ovat vain symboleja, jotka tarkoittavat jotakin tuntematonta lukua tai arvoa, joten voit käyttää mitä tahansa kirjainta muuttujaa varten (paitsi e {\displaystyle e} $e$ (Eulerin luku) ja i {\displaystyle i} $i$ (kuvitteellinen yksikkö), koska nämä ovat matemaattisia vakioita). x {\displaystyle x} ja y {\displaystyle y} ovat kuitenkin yleisimpiä.

Funktiot ja kuvaajat

Tärkeä osa algebraa on funktioiden tutkiminen, sillä ne esiintyvät usein yhtälöissä, joita yritämme ratkaista. Funktio on ikään kuin kone, johon voi laittaa luvun (tai lukuja) ja josta saa tietyn luvun (tai lukuja). Kun käytetään funktioita, kuvaajat voivat olla tehokkaita apuvälineitä yhtälöiden ratkaisujen tutkimisessa.

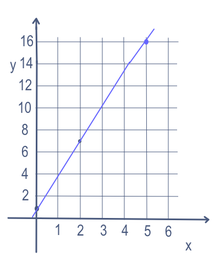
Kuvaaja on kuva, jossa näkyvät kaikki muuttujien arvot, jotka tekevät yhtälöstä tai epätasa-arvosta todellisen. Yleensä tämä on helppo tehdä, kun muuttujia on vain yksi tai kaksi. Kuvaaja on usein viiva, ja jos viiva ei taivu tai kulje suoraan ylös-alas, sitä voidaan kuvata peruskaavalla y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Muuttuja b {\displaystyle b} $b$ on kuvaajan y-katkoviiva (missä viiva ylittää pystyakselin) ja m {\displaystyle m} on viivan kaltevuus tai jyrkkyys. Tätä kaavaa sovelletaan kuvaajan koordinaatteihin, joissa jokainen suoran piste kirjoitetaan ( x {\displaystyle x} , y {\displaystyle y} ).

Joissakin matemaattisissa ongelmissa, kuten viivan yhtälössä, voi olla useampi kuin yksi muuttuja (tässä tapauksessa x {\displaystyle x} ja y {\displaystyle y} ). Suoran pisteiden löytämiseksi yhtä muuttujaa muutetaan. Muutettua muuttujaa kutsutaan "riippumattomaksi" muuttujaksi. Sitten tehdään matematiikka, jotta saadaan luku. Muodostettua lukua kutsutaan "riippuvaksi" muuttujaksi. Useimmiten riippumaton muuttuja kirjoitetaan muodossa x {\displaystyle x} ja riippuvainen muuttuja muodossa y {\displaystyle y}. , esimerkiksi y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$ . Tämä asetetaan usein kuvaajaan käyttämällä x {\displaystyle x} -akselia (vasemmalle ja oikealle) ja y {\displaystyle y} -akselia (ylös ja alas). Se voidaan kirjoittaa myös funktiona: f ( x ) = 3 x + 1 {\displaystyle f(x)=3x+1} $f(x)=3x+1$ . Tässä esimerkissä voimme siis laittaa x:n arvoksi 5 {\displaystyle x} ja saada y = 16 {\displaystyle y=16} $y=16$ . Laitetaan x:lle 2 {\displaystyle x} ja saadaan y = 7 {\displaystyle y=7} $y=7$ . Ja 0 x:lle {\displaystyle x} saisi y = 1 {\displaystyle y=1} $y=1$ . Pisteiden (5,16), (2,7) ja (0,1) kautta kulkee siis viiva, kuten oikealla olevassa kuvaajassa näkyy.

Jos x {\displaystyle x} on potenssi 1, se on suora. Jos se on neliö tai jokin muu potenssi, se on kaareva. Jos siinä käytetään epäyhtälöä ( < {\displaystyle <} $<$ tai > {\displaystyle >} $>$ ), yleensä osa kuvaajasta varjostetaan, joko viivan ylä- tai alapuolella.

Lineaarinen yhtälö y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$

Säännöt

Algebrassa on muutamia sääntöjä, joita voidaan käyttää yhtälöiden ymmärtämiseen. Näitä kutsutaan algebran säännöiksi. Vaikka nämä säännöt saattavat tuntua järjettömiltä tai ilmeisiltä, on viisasta ymmärtää, että nämä ominaisuudet eivät päde kaikilla matematiikan aloilla. Siksi on hyödyllistä tietää, miten nämä aksiomaattiset säännöt julistetaan, ennen kuin pitää niitä itsestäänselvyyksinä. Ennen kuin siirrytään sääntöihin, pohdi kahta määritelmää, jotka annetaan.

Vastakohta: {\displaystyle a} vastakohta on - {\displaystyle -a} .
Vastavuoroinen: {\displaystyle a} vastavuoroinen on 1 a {\displaystyle {\frac {1}{a}}} . ${\frac {1}{a}}$

Yhteenlaskun kommutatiivinen ominaisuus

'Kommutatiivinen' tarkoittaa, että funktio saa saman tuloksen, jos numerot vaihdetaan. Toisin sanoen yhtälön termien järjestyksellä ei ole merkitystä. Kun kaksi termiä (yhteenlaskua) lasketaan yhteen, sovelletaan yhteenlaskun kommutatiivista ominaisuutta. Algebrassa tämä tarkoittaa, että a + b = b + a {\displaystyle a+b=b+a} . a+b=b+a

Huomaa, että tämä ei päde vähennyslaskuun (eli a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ paitsi jos a = b {\displaystyle a=b} $a=b$ ).

Kertolaskun kommutatiivinen ominaisuus

Kun kaksi termiä (tekijää) kerrotaan, sovelletaan kertolaskun kommutatiivista ominaisuutta. Algebrassa tämä tarkoittaa, että a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} . $a\cdot b=b\cdot a$

Huomaa, että tämä ei päde jakamiseen (eli a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}). ${\frac {a}{b}}\neq {\frac {b}{a}}$ , kun a ≠ 0 {\displaystyle a\neq 0} $a\neq 0$ ja b ≠ 0 {\displaystyle b\neq 0} $b\neq 0$ , paitsi jos a = b {\displaystyle a=b} $a=b$ ).

Yhteenlaskun assosiatiivinen ominaisuus

'Assosiatiivinen' tarkoittaa numeroiden ryhmittelyä. Yhteenlaskun assosiatiivinen ominaisuus tarkoittaa, että kun lasketaan yhteen kolme tai useampia termejä, ei ole väliä, miten nämä termit on ryhmitelty. Algebrallisesti tämä antaa a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Huomaa, että tämä ei päde vähennyslaskussa, esim. 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {\displaystyle 1-(2-3)\neq (1-2)-3} $1-(2-3)\neq (1-2)-3$ (katso distributiivinen ominaisuus).

Kertolaskun assosiatiivinen ominaisuus

Kertolaskun assosiatiivinen ominaisuus tarkoittaa, että kun kerrotaan kolme tai useampia termejä, ei ole väliä, miten nämä termit on ryhmitelty. Algebrallisesti tämä antaa a ( b c ) = ( a b ) c {\displaystyle a(bc)=(ab)c} $a(bc)=(ab)c$ . Huomaa, että tämä ei päde jaettaessa, esim. 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} . $1/(2/4)\neq (1/2)/4$

Jako-ominaisuus

Jako-ominaisuuden mukaan termin kertominen toisella termillä voidaan jakaa. Esimerkiksi: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} $a(b+c)=ab+ac$ . (Älä sekoita tätä assosiatiivisiin ominaisuuksiin! Esimerkiksi: a ( b + c ) ≠ ( a b ) + c {\displaystyle a(b+c)\neq (ab)+c} $a(b+c)\neq (ab)+c$ .)

Additiivinen identiteetti

'Identtisyys' tarkoittaa luvun ominaisuutta, jonka mukaan se on yhtä suuri kuin itse itsensä. Toisin sanoen, on olemassa kahden luvun operaatio, joka on yhtä suuri kuin summan muuttuja. Additiivinen identtisyysominaisuus sanoo, että mikä tahansa luku plus 0 on kyseinen luku: a + 0 = a {\displaystyle a+0=a} a+0=a . Tämä pätee myös vähennyslaskussa: a - 0 = a {\displaystyle a-0=a} a-0=a .

Multiplikatiivinen identiteetti

Kertolaskennan identiteettiominaisuus sanoo, että mikä tahansa luku kertaa 1 on tämä luku: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Tämä pätee myös jaettaessa: a 1 = a {\displaystyle {\frac {a}{1}}=a} . ${\frac {a}{1}}=a$

Additiivinen käänteisominaisuus

Additiivinen käänteisominaisuus on ikään kuin additiivisen identiteetin vastakohta. Kun laskemme yhteen luvun ja sen vastakohdan, tuloksena on 0. Algebrallisesti se tarkoittaa seuraavaa: a + - a = 0 {\displaystyle a+-a=0} $a+-a=0$ , mikä on sama kuin a - a = 0 {\displaystyle a-a=0} $a-a=0$ . Esimerkiksi 1:n additiivinen käänteisluku (tai vastakohta) on -1.

Multiplikatiivinen käänteisominaisuus

Kertolaskennan käänteisominaisuus tarkoittaa, että kun kerromme luvun ja sen käänteisluvun keskenään, tulos on 1. Algebrallisesti se tarkoittaa seuraavaa: a ⋅ $a\cdot {\frac {1}{a}}=1$ , mikä on sama kuin a a = 1 {\displaystyle {\frac {a}{a}}=1} ${\frac {a}{a}}=1$ . Esimerkiksi 2:n multiplikatiivinen käänteisluku (tai vain käänteisluku) on 1/2. Murtoluvun käänteisluku saadaan vaihtamalla osoittaja ja nimittäjä: 2 3 {\displaystyle {\frac {2}{3}}} ${\frac {2}{3}}$ käänteisluku on 3 2 {\displaystyle {\frac {3}{2}}} . ${\frac {3}{2}}$

Edistynyt algebra

Alkeisalgebran eli perusalgebran lisäksi on olemassa korkeakouluissa ja yliopistoissa opetettavia algebran edistyneempiä muotoja, kuten abstraktia algebraa, lineaarialgebraa ja yleisalgebraa. Tähän kuuluu myös se, miten matriisin avulla voidaan ratkaista useita lineaarisia yhtälöitä kerralla. Abstraktissa algebrassa tutkitaan yhtälöissä esiintyviä asioita ja mennään numeroita pidemmälle abstraktimpaan numeroryhmien kanssa.

Monet matematiikan ongelmat liittyvät fysiikkaan ja tekniikkaan. Monissa näistä fysiikan ongelmista aika on muuttuja. Ajan kirjain on t {\displaystyle t} $t$ . Algebran perusajatusten käyttäminen voi auttaa vähentämään matemaattisen ongelman yksinkertaisimpaan muotoonsa, jolloin vaikeiden ongelmien ratkaiseminen helpottuu. Energia on e {\displaystyle e} $e$ , voima on f {\displaystyle f} , massa on m {\displaystyle m} . , kiihtyvyys on a {\displaystyle a} ja valon nopeus on joskus c {\displaystyle c} $c$ . Tätä käytetään joissakin tunnetuissa yhtälöissä, kuten f = m a {\displaystyle f=ma} $f=ma$ ja e = m c 2 {\displaystyle e=mc^{2}} $e=mc^{2}$ (vaikka viimeksi mainitun yhtälön keksimiseen tarvittiin algebraa monimutkaisempaa matematiikkaa).

Aiheeseen liittyvät sivut

Luettelo matematiikan aiheista
Toimintajärjestys
Parabeli
Tietokonealgebrajärjestelmä

Kysymyksiä ja vastauksia

K: Mitä on algebra?

V: Algebra on osa matematiikkaa, jossa käytetään muuttujia edustamaan arvoa, jota ei vielä tunneta.

K: Mitä yhtäsuuruusmerkki tarkoittaa algebrassa?

V: Yhtälön merkki (=) tarkoittaa algebrassa yhtälöä.

K: Mikä on funktio algebrassa?

V: Funktio algebrassa on erityyppinen yhtälö, joka muuttaa aina yhden syötteen yhdeksi tuloksi.

K: Miten algebraa voidaan käyttää todellisten ongelmien ratkaisemiseen?

V: Algebraa voidaan käyttää todellisten ongelmien ratkaisemiseen, koska algebran säännöt toimivat todellisessa elämässä ja numeroita voidaan käyttää todellisten asioiden arvojen esittämiseen. Fysiikka, tekniikka ja tietokoneohjelmointi ovat aloja, joilla algebraa käytetään jatkuvasti. Algebraa on hyödyllistä osata myös maanmittauksessa, rakentamisessa ja liike-elämässä, erityisesti kirjanpidossa.

Kysymys: Mitä matemaattisia operaatioita käytetään numeroilla algebrassa?

V: Algebrassa käytetään lukujen sääntöjä ja matemaattisia operaatioita, kuten lisääminen, vähentäminen, kertominen ja jakaminen. Edistyneemmissä operaatioissa käytetään eksponentteja, alkaen neliöistä ja neliöjuurista.

K: Mitkä ovat esimerkkejä algebrassa käytettävistä yhtälöistä?

V: Esimerkkejä algebrassa käytetyistä yhtälöistä ovat lineaariset yhtälöt (suoran yhtälö) ja kvadraattiset yhtälöt, joiden muuttujat ovat neliöitä (kerrottu itsellään).

Etsiä

Algebra — määritelmä, yhtälöt, funktiot ja käytännön sovellukset

Mikä on algebra käytännössä?

Yhtälöt ja muuttujan ratkaiseminen

Funktiot ja kuvaajat

Epätasa-arvot

Yleisimpiä yhtälötyyppejä

Perussäännöt ja operaatiot

Käytännön sovelluksia

Esimerkkejä arjen tehtävistä

Miten oppia algebraa tehokkaasti

Historia

Esimerkkejä

Kirjoitusalgebra

Funktiot ja kuvaajat

Säännöt

Yhteenlaskun kommutatiivinen ominaisuus

Kertolaskun kommutatiivinen ominaisuus

Yhteenlaskun assosiatiivinen ominaisuus

Kertolaskun assosiatiivinen ominaisuus

Jako-ominaisuus

Additiivinen identiteetti

Multiplikatiivinen identiteetti

Additiivinen käänteisominaisuus

Multiplikatiivinen käänteisominaisuus

Edistynyt algebra

Aiheeseen liittyvät sivut

Kysymyksiä ja vastauksia

K: Mitä on algebra?

K: Mitä yhtäsuuruusmerkki tarkoittaa algebrassa?

K: Mikä on funktio algebrassa?

K: Miten algebraa voidaan käyttää todellisten ongelmien ratkaisemiseen?

Kysymys: Mitä matemaattisia operaatioita käytetään numeroilla algebrassa?

K: Mitkä ovat esimerkkejä algebrassa käytettävistä yhtälöistä?

Hae kirjaimella