Graafiteoria | matematiikan ala, joka käsittelee graafeja
Graafiteoria on matematiikan ala, joka käsittelee graafeja. Graafi on abstrakti esitys, jossa on: joukko pisteitä, jotka ovat yhteydessä toisiinsa viivoilla. Jokaista pistettä kutsutaan yleensä pisteeksi (useampia pisteitä kutsutaan kärkipisteiksi), ja viivoja kutsutaan reunoiksi. Graafit ovat väline suhteiden mallintamiseen. Niitä käytetään vastausten löytämiseen moniin ongelmiin.
Joitakin näistä kysymyksistä ovat:
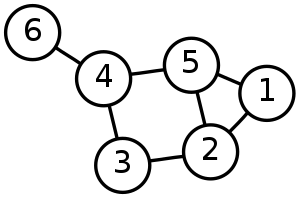
Suuntaamaton graafi.
Erilaiset kuvaajat
- Graafiteorialla on monia näkökohtia. Graafit voivat olla suunnattuja tai suuntaamattomia. Esimerkki suunnatusta graafista olisi kaupungin tiejärjestelmä. Jotkin kaupungin kadut ovat yksisuuntaisia. Tämä tarkoittaa, että näillä osuuksilla on vain yksi suunta.
- Graafeja voidaan painottaa. Esimerkkinä voidaan mainita tieverkko, jossa on etäisyyksiä tai tiemaksuja (teiden osalta).
- Graafin solmuja (ympyrät kaaviossa) kutsutaan kärkipisteiksi. Solmuja yhdistäviä viivoja kutsutaan reunoiksi. Kahden solmun välillä ei voi olla yhtään viivaa, voi olla yksi viiva tai voi olla useita viivoja.
- Graafiteoriassa käytetään laajalti Trees-rakenteita, jotka edustavat hierarkkisia rakenteita. Puu on suunnattu tai suuntaamaton graafi, jossa ei ole sykliä, mikä tarkoittaa, että yhdestä pisteestä (esimerkiksi kaupungista) ei pääse samaan pisteeseen käyttämällä jokaista reunaa vain kerran (kävelemällä vain kerran jokaista tietä pitkin).
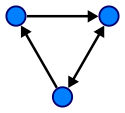
Suunnattu graafi.
Historia
→
→ 
Königbergin seitsemän sillan visualisointi. Leonhard Euler ratkaisi tämän ongelman vuonna 1736, mikä johti topologian ja modernin graafiteorian kehittymiseen.
Graafi on abstrakti tietorakenne. Se sisältää solmuja, jotka yleensä liittyvät toisiinsa. Solmu on tietokokonaisuus, joka on tyypillisesti järjestettyjen parien muodossa. Solmut ovat joko yhteydessä toisiin solmuihin tai eivät ole yhteydessä toisiin solmuihin. Solmujen välinen suhde määritellään yleensä reunaksi (Edge). Graafit ovat hyödyllisiä, koska ne pystyvät yhdistämään solmuja toisiin solmuihin. Käytännössä graafeilla on muutamia esitystapoja.
Leonhard Euler asui Königsberg-nimisessä kaupungissa. (Sen nimi muuttui Kaliningradiksi vuonna 1946). Kaupunki sijaitsee Pregel-joen varrella. Joessa on saari. Joen yli on joitakin siltoja. Euler halusi kävellä ympäri ja käyttää jokaista siltaa kerran. Hän kysyi, voisiko hän tehdä sen. Vuonna 1736 hän julkaisi tieteellisen artikkelin, jossa hän osoitti, että tämä ei ollut mahdollista. Nykyään tämä ongelma tunnetaan Königsbergin seitsemänä siltana. Artikkelia pidetään ensimmäisenä artikkelina graafiteorian historiassa.
Tämä artikkeli, samoin kuin Vandermonden kirjoittama artikkeli ritari-ongelmasta, jatkoi Leibnizin aloittamaa analyysia situs. Eulerin kaavaa, joka koski kuperan monitahokkaan reunojen, kärkipisteiden ja kasvojen lukumäärää, tutkivat ja yleistivät Cauchy ja L'Huillier, ja se on topologian alkulähteillä.
Matematiikasta ja kemiasta peräisin olevien ajatusten yhdistäminen on saanut alkunsa osasta graafiteorian vakioterminologiaa. Erityisesti Sylvester otti käyttöön termin "graafi" vuonna 1878 Nature-lehdessä julkaistussa artikkelissa.
Yksi graafiteorian tunnetuimmista ja tuottavimmista ongelmista on neljän värin ongelma: "Onko totta, että minkä tahansa tasoon piirretyn kartan alueet voidaan värittää neljällä värillä siten, että kahdella alueella, joilla on yhteinen raja, on eri värit?".
Sama ongelma, mutta kuvaajan avulla
Königsbergin siltaongelma kaupungin kartalla
Graafiteoria perspektiivissä
Graafiteoria on tärkeä osa matematiikkaa ja tietotekniikkaa. Moniin tällaisiin ongelmiin on olemassa täsmällisiä ratkaisuja. Usein niitä on kuitenkin hyvin vaikea laskea. Sen vuoksi käytetään hyvin usein approksimaatioita. Tällaisia approksimaatioita on kahdenlaisia, Monte-Carlo-algoritmeja ja Las-Vegas-algoritmeja.
Kysymyksiä ja vastauksia
K: Mitä on graafiteoria?
V: Graafiteoria on matematiikan ala, joka tutkii graafeja, jotka ovat viivoilla yhdistettyjen pisteiden abstrakteja esityksiä.
K: Millä nimellä graafin pisteitä kutsutaan?
V: Graafin pisteitä kutsutaan yleensä kärkipisteiksi.
K: Mitä kärkipisteiden väliset viivat edustavat?
V: Pisteiden väliset viivat kuvaavat niiden välisiä suhteita tai yhteyksiä.
K: Miten kuvaajia voidaan käyttää?
V: Graafien avulla voidaan mallintaa suhteita ja löytää vastauksia erilaisiin ongelmiin.
K: Millaisiin kysymyksiin kuvaajat voivat auttaa vastaamaan?
V: Graafit voivat auttaa vastaamaan verkkoanalyysiin, optimointiin ja aikataulutukseen liittyviin kysymyksiin.
K: Onko olemassa erityyppisiä kuvaajia?
V: Kyllä, on olemassa erityyppisiä graafeja, kuten suunnattuja ja suuntaamattomia graafeja, painotettuja ja painottamattomia graafeja, täydellisiä ja epätäydellisiä graafeja jne.
K: Onko saatavilla ohjelmia, joilla voi työskennellä graafiteorian parissa?
V: Kyllä, graafiteorian käsittelyyn on saatavilla ohjelmistoja, kuten Gephi ja NetworkX.
