Neliväriongelma | Matematiikan teoreema
Neljän värin lause on matematiikan lause. Sen mukaan missä tahansa tasopinnassa, jossa on alueita (ihmiset ajattelevat niitä karttoina), alueet voidaan värittää enintään neljällä värillä. Kaksi aluetta, joilla on yhteinen raja, eivät saa saada samaa väriä. Niitä kutsutaan vierekkäisiksi (vierekkäisiksi), jos niillä on yhteinen rajapinta, ei vain piste.
Tämä oli ensimmäinen tietokoneella todistettu teoreema, joka todistettiin uupumuksen avulla. Uupumustodistuksessa johtopäätös vahvistetaan jakamalla se tapauksiin ja todistamalla jokainen tapaus erikseen. Tapauksia voi olla paljon. Esimerkiksi neliväriteoremin ensimmäinen todistus oli uuvuttamistodistus, jossa oli 1 936 tapausta. Tämä todistus oli kiistanalainen, koska suurin osa tapauksista tarkistettiin tietokoneohjelmalla eikä käsin. Lyhyimmässä tunnetussa neljän värin teoreeman todistuksessa on vielä nykyäänkin yli 600 tapausta.
Vaikka ongelma esitettiin alun perin maiden poliittisten karttojen värittämiseen liittyvänä ongelmana, kartantekijät eivät ole siitä kovin kiinnostuneita. Matematiikkahistorioitsija Kenneth Mayn artikkelin (Wilson 2002, 2) mukaan "kartat, joissa käytetään vain neljää väriä, ovat harvinaisia, ja ne, joissa käytetään, vaativat yleensä vain kolme väriä. Kartografiaa ja kartanvalmistuksen historiaa käsittelevissä kirjoissa ei mainita neliväriominaisuutta."
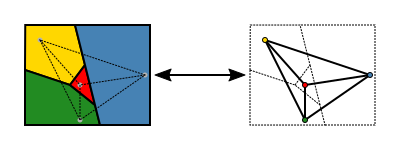
Monet yksinkertaisemmat kartat voidaan värittää kolmella värillä. Neljättä väriä tarvitaan joihinkin karttoihin, kuten karttoihin, joissa yhtä aluetta ympäröi pariton määrä muita alueita, jotka koskettavat toisiaan syklinä. Yksi tällainen esimerkki on esitetty kuvassa. Viiden värin lauseen mukaan viisi väriä riittää kartan värittämiseen. Sen todistus on lyhyt ja alkeellinen, ja se todistettiin 1800-luvun lopulla. (Heawood 1890) Sen todistaminen, että tarvitaan vain neljä väriä, osoittautui paljon vaikeammaksi. Neljän värin teoreeman ensimmäisen toteamuksen jälkeen vuonna 1852 on ilmestynyt monia vääriä todistuksia ja vääriä vastaesimerkkejä.
Kolme väriä ei riitä tämän kartan värittämiseen.
Esimerkki nelivärikartasta
Ongelman tarkka muotoilu
Intuitiivisesti neljän värin teoreema voidaan esittää seuraavasti: "Kun taso on jaettu vierekkäisiin alueisiin, joita kutsutaan kartaksi, alueet voidaan värittää enintään neljällä värillä siten, että millään kahdella vierekkäisellä alueella ei ole samaa väriä". Jotta ongelma voitaisiin ratkaista oikein, on tarpeen selventää joitakin näkökohtia: Ensinnäkin kaikki kolmeen tai useampaan maahan kuuluvat pisteet on jätettävä huomiotta. Toiseksi, oudot kartat, joissa on pinta-alaltaan rajallisia ja kehältään äärettömiä alueita, voivat vaatia enemmän kuin neljä väriä.
Lauseen soveltamiseksi jokaisen "maan" on oltava yksinkertaisesti yhdistetty alue tai vierekkäinen. Todellisessa maailmassa tämä ei pidä paikkaansa: Alaska osana Yhdysvaltoja, Nakhchivan osana Azerbaidžania ja Kaliningrad osana Venäjää eivät ole yhtenäisiä. Koska tietyn maan alueen on oltava samanvärinen, neljä väriä ei välttämättä riitä. Tarkastellaan esimerkiksi vasemmalla olevan kaltaista yksinkertaistettua karttaa: Tässä kartassa kaksi aluetta, jotka on merkitty A:lla, kuuluvat samaan maahan, ja niiden on oltava samanvärisiä. Tämä kartta vaatii viisi väriä, koska kaksi A:n aluetta rajoittuu neljään muuhun alueeseen, joista jokainen rajoittuu kaikkiin muihin alueisiin. Jos A:lla olisi vain kolme aluetta, tarvittaisiin kuusi tai enemmän värejä. Tällä tavoin on mahdollista tehdä karttoja, jotka tarvitsevat mielivaltaisen suuren määrän värejä. Samanlainen rakenne pätee myös, jos kaikille vesistöille käytetään yhtä väriä, kuten todellisissa kartoissa on tavallista.
Helpommin esitettävä versio lauseesta käyttää graafiteoriaa. Kartan alueiden joukko voidaan esittää abstraktimmin suuntaamattomana graafina, jossa jokaisella alueella on oma huippunsa ja jokaisella rajaparilla on oma reunansa. Graafi on tasomainen: se voidaan piirtää tasoon ilman risteyksiä sijoittamalla kukin huippu mielivaltaisesti valittuun paikkaan sen alueen sisällä, jota se vastaa, ja piirtämällä reunat käyrinä, jotka johtavat ilman risteyksiä kunkin alueen sisällä huippupisteen sijainnista kuhunkin alueen yhteiseen rajapisteeseen. Kääntäen mikä tahansa tasograafi voidaan muodostaa kartasta tällä tavoin. Graafiteoreettisessa terminologiassa neliväriteorema sanoo, että jokaisen tasograafin kärkipisteet voidaan värjätä enintään neljällä värillä niin, että millään kahdella vierekkäisellä kärkipisteellä ei ole samaa väriä, tai lyhyesti sanottuna "jokainen tasograafi on nelivärinen" (Thomas 1998, s. 849; Wilson 2002).
Esimerkki Azerbaidžanin kartasta, jossa ei ole yhtenäisiä alueita.
Tätä karttaa ei voi värittää neljällä värillä
Historia
Ensimmäisenä ongelman nimesi Francis Guthrie vuonna 1852. Hän oli tuolloin oikeustieteen opiskelija Englannissa. Hän huomasi, että hän tarvitsi vähintään neljä väriä värittääkseen kartan Englannin kreivikunnista. Augustus de Morgan käsitteli ongelmaa ensimmäisen kerran kirjeessä, jonka hän kirjoitti Rowan Hamlitonille elokuussa 1852. Kirjeessä de Morgan kysyy, riittääkö neljä väriä todella kartan värittämiseen siten, että vierekkäin olevat maat saavat eri värit.
Englantilainen matemaatikko Arthur Cayley esitteli ongelman Lontoossa vuonna 1878 pidetyssä matemaattisessa seurassa. Vuoden kuluessa Alfred Kempe löysi ongelman todisteelta näyttävän ratkaisun. Yksitoista vuotta myöhemmin, vuonna 1890, Percy Heawood osoitti, että Alfredin todistus oli väärä. Peter Guthrie Tait esitti toisen todistusyrityksen vuonna 1880. Kesti yksitoista vuotta osoittaa, että Taitin todiste ei myöskään toiminut. Vuonna 1891 Julius Petersen pystyi osoittamaan tämän. Kun hän väärensi Cayleyn todistuksen, Kempe osoitti myös todistuksen ongelmalle, jota hän kutsui Viiden värin lauseeksi. Teoreema sanoo, että mikä tahansa tällainen kartta voidaan värittää korkeintaan viidellä värillä. Rajoituksia on kaksi: Ensinnäkin, mikä tahansa maa on yhtenäinen, ei ole eksklaaveja. Toinen rajoitus on se, että mailla on oltava yhteinen raja; jos ne koskettavat toisiaan vain pisteessä, ne voidaan värittää samalla värillä. Vaikka Kempin todistus oli väärä, hän käytti joitakin ajatuksia, jotka myöhemmin mahdollistivat oikean todistuksen.
Heinrich Heesch kehitti 1960- ja 1970-luvuilla ensimmäisen luonnoksen tietokoneella tehtävästä todistuksesta. Kenneth Appel ja Wolfgang Haken paransivat tätä luonnosta vuonna 1976 (Robertson et al. 1996). He pystyivät vähentämään testattavien tapausten määrän 1936:een; myöhemmin tehtiin versio, joka perustui vain 1476 tapauksen testaamiseen. Jokainen tapaus oli testattava tietokoneella (Appel & Haken 1977) harv virhe: useita kohteita (2×): CITEREFAppelHaken1977 (ohje).
Vuonna 1996 Neil Robertson, Daniel Sanders, Paul Seymour ja Robin Thomas paransivat menetelmää ja vähensivät testattavien tapausten määrän 663:een. Jälleen jokainen tapaus oli testattava tietokoneella.
Vuonna 2005 Georges Gonthier ja Benjamin Werner kehittivät muodollisen todistuksen. Tämä oli parannus, koska sen avulla voitiin ensimmäistä kertaa käyttää teoreemantarkistusohjelmia. Käytetty ohjelmisto on nimeltään Coq.
Neljän värin lause on ensimmäinen suuri matemaattinen ongelma, joka todistettiin tietokoneen avulla. Koska todistusta ei voi tehdä ihminen, jotkut matemaatikot eivät tunnustaneet sitä oikeaksi. Todistuksen todentaminen edellyttää oikein toimivaa ohjelmistoa ja laitteistoa, jotta todistus voidaan todentaa. Koska todistus tehtiin tietokoneella, se ei myöskään ole kovin tyylikäs.
Virheellisiksi osoittautuneet yritykset
Neliväriteoria on ollut tunnettu siitä, että sen pitkän historian aikana on tehty paljon vääriä todistuksia ja kumoamisia. Aluksi The New York Times kieltäytyi raportoimasta Appel-Hakenin todistuksesta. Sanomalehti teki näin politiikkansa vuoksi; se pelkäsi, että todistus osoittautuisi vääräksi kuten aiemmat todistukset (Wilson 2002, s. 209). Joissakin todistuksissa kesti kauan, ennen kuin ne voitiin väärentää: Kempin ja Taitin todisteiden väärentäminen kesti yli kymmenen vuotta.
Yksinkertaisimmissa vastakohdissa yritetään yleensä luoda yksi alue, joka koskettaa kaikkia muita alueita. Tämä pakottaa jäljelle jäävät alueet värittämään vain kolmella värillä. Koska neljän värin lause on tosi, tämä on aina mahdollista; koska kartan piirtäjä kuitenkin keskittyy yhteen suureen alueeseen, hän ei huomaa, että loput alueet voidaan itse asiassa värittää kolmella värillä.
Tämä temppu voidaan yleistää: Jos kartan joidenkin alueiden värit valitaan etukäteen, on mahdotonta värittää loput alueet siten, että yhteensä käytetään vain neljää väriä. Joku, joka todentaa vastaesimerkin, ei välttämättä ajattele, että näiden alueiden värien muuttaminen voi olla tarpeen. Tämä saa vastaesimerkin näyttämään pätevältä, vaikka se ei ole sitä.
Ehkä yksi tämän yleisen väärinkäsityksen taustalla oleva vaikutus on se, että värirajoitus ei ole transitiivinen: alueen on oltava erivärinen vain alueista, joita se koskettaa suoraan, ei alueista, jotka koskettavat alueita, joita se koskettaa. Jos tämä olisi rajoitus, tasograafit vaatisivat mielivaltaisen suuren määrän värejä.
Muut väärät kumoamiset rikkovat teoreeman oletuksia odottamattomilla tavoilla, kuten käyttämällä aluetta, jolla on useita irrallisia osia, tai estämällä samanväristen alueiden koskettamisen pisteessä.
Kartta (vasemmalla) on väritetty viidellä värillä, ja on tarpeen muuttaa vähintään neljää kymmenestä alueesta, jotta saataisiin väritys, jossa on vain neljä väriä (oikealla).
Poliittisten karttojen värittäminen
Tosielämässä monilla mailla on eksklavia- tai siirtomaavaltioita. Koska ne kuuluvat maahan, ne on värjättävä samalla värillä kuin emämaa. Tämä tarkoittaa, että yleensä tällaisen kartan värittämiseen tarvitaan enemmän kuin neljä väriä. Kun matemaatikot puhuvat ongelmaan liittyvästä kuvaajasta, he sanovat, että se ei ole tasomainen. Vaikka on helppo tarkistaa, onko kuvaaja tasainen, on hyvin vaikeaa löytää vähiten värejä, joita tarvitaan sen värittämiseen. Se on NP-täydellinen, mikä on yksi vaikeimmista olemassa olevista ongelmista. Graafin värittämiseen tarvittavien värien vähintä määrää kutsutaan kromaattiseksi luvuksi. Monet ongelmat, joita esiintyy, kun yritetään ratkaista neljän värin teoreemaa, liittyvät diskreettiin matematiikkaan. Tästä syystä käytetään usein algebrallisen topologian menetelmiä.
Laajennus "ei-tasaisiin" karttoihin
Neljän värin lause edellyttää, että "kartta" on tasaisella pinnalla, jota matemaatikot kutsuvat tasoksi. Vuonna 1890 Percy John Heawood loi sen, mitä nykyään kutsutaan Heawoodin konjektuuriksi: Siinä esitetään sama kysymys kuin neliväriteoriassa, mutta mille tahansa topologiselle kohteelle. Esimerkiksi torus voidaan värittää enintään seitsemällä värillä. Heawoodin konjektuuri antaa kaavan, joka toimii kaikille tällaisille kohteille, paitsi Kleinin pullolle.
Kysymyksiä ja vastauksia
K: Mikä on neljän värin lause?
A: Neliväriteoreema on matemaattinen teoreema, jonka mukaan missä tahansa tasopinnassa, jossa on alueita, alueet voidaan värittää enintään neljällä värillä. Vierekkäiset alueet eivät saa saada samaa väriä.
K: Miten neljän värin teoreeman ensimmäinen todistus laadittiin?
V: Neljän värin teoreeman ensimmäinen todistus oli 1 936 tapausta käsittävä uupumistodistus. Tämä tarkoittaa, että se vahvistettiin jakamalla se tapauksiin ja todistamalla jokainen tapaus erikseen.
K: Kiinnostaako tämä ongelma kartantekijöitä?
V: Ei, kartantekijät eivät ole kovin kiinnostuneita tästä ongelmasta, sillä kartat, joissa käytetään vain neljää väriä, ovat harvinaisia ja vaativat yleensä vain kolme väriä. Kartografiaa ja kartanvalmistuksen historiaa käsittelevissä kirjoissa ei mainita neliväriominaisuutta.
K: Mikä on viiden värin teoreema?
V: Viiden värin teoreeman mukaan viisi väriä riittää kartan värittämiseen, ja sille on lyhyt, alkeellinen todiste, joka todistettiin 1800-luvun lopulla.
K: Kuinka vaikeaa oli todistaa, että karttojen värittämiseen tarvitaan vain neljä väriä?
V: Sen todistaminen, että karttojen värittämiseen tarvitaan vain neljä väriä, osoittautui paljon odotettua vaikeammaksi, sillä sen jälkeen, kun lause todettiin ensimmäisen kerran vuonna 1852, on ilmestynyt monia vääriä todistuksia ja vääriä vastaesimerkkejä.
Kysymys: Onko olemassa esimerkki kartasta, jossa tarvittaisiin 5 tai enemmän värejä, jotta kaikki alueet voitaisiin värittää oikein?
V: Kyllä, yksi tällainen esimerkki on, kun yhtä aluetta ympäröi pariton määrä muita alueita, jotka koskettavat toisiaan syklinä - tässä tapauksessa kaikkien alueiden värittämiseen oikein voi tarvita 5 tai useampia värejä.
