Keplerin lait – planeettojen liikkeen kolme peruslakia
Keplerin lait selitetty: kolme peruslakia planeettojen elliptisistä kiertoradoista, liikesuhteista ja kaavoista – havainnollinen johdanto Johannes Keplerin löydöksiin.
Keplerin planeettojen liikkeen lait ovat kolme lakia, jotka kuvaavat planeettojen liikettä auringon ympäri:
- Planeetat liikkuvat auringon ympäri elliptisillä kiertoradoilla. Aurinko on jommassakummassa radan polttopisteessä.
- Planeetan ja Auringon yhdistävä viivasegmentti pyyhkäisee yhtä suuria alueita yhtä suurina aikaväleinä.
- Planeetan kiertoradan jakson neliö on verrannollinen sen kiertoradan puoli-suurakselin kuutioon.
Johannes Kepler löysi nämä lait vuosina 1609-1619.
Selitykset ja lisätiedot
Ensimmäinen laki — elliptinen rata: Ellipsi on geometrinen käyrä, jolla on kaksi polttopistettä (fokusta). Keplerin ensimmäisen lain mukaan planeetan rata ei ole pakollisesti ympyrä vaan ellipsi, ja Aurinko sijaitsee ellipsin yhdessä polttopisteessä. Kiertoradan muotoa kuvataan eksentrisyydellä e (0 =< e < 1 elliptiselle radalle): e = 0 vastaa ympyrää, suurempi e tarkoittaa pitkulaisempaa ellipsiä. Radiaalietäisyys kulmassa θ voidaan ilmaista esim. muodossa r = a(1 − e^2) / (1 + e cos θ), missä a on puoli-suurakseli.
Toinen laki — pinta-alat: Laki sanoo, että suora viiva joka yhdistää planeetan ja Auringon pyyhkii yhtä suuria alueita yhtä suurina aikaväleinä. Tämä tarkoittaa, että planeetan nopeus ei ole vakio: se liikkuu nopeimmin perihelissä (lähellä Aurinkoa) ja hitaimmin afelissä (kauimpana). Ilmiö voidaan johtaa kulmamomentin säilymisestä: areaalinopeus r^2 dθ/dt on vakio puolisuperheiselle kahden kappaleen liikkeelle.\
Kolmas laki — aika ja puoli-suurakseli: Kolmannen lain matemaattinen muoto on T^2 ∝ a^3, jossa T on kiertoaika (periodi) ja a puoli-suurakseli. Aurinkokunnassa, jos käytetään vuosia ja astronomisia yksiköitä (1 AU = Maan etäisyys Auringosta), suhde yksinkertaistuu hyvin lähelle muotoa T^2 = a^3. Yleisemmässä kaksikehäisessä gravitaatiotapauksessa Newtonin lain nojalla pätee tarkemmin T^2 = (4π^2/GM) a^3, missä G on gravitaatiovakio ja M keskuskappaleen massa (esim. Auringon massa). Tämä kolmas laki yhdistää avaruudellisen mittakaavan (a) ja ajallisen mittakaavan (T).
Historiallinen ja teoreettinen merkitys
Kepler johdatti lakinsa analysoimalla Tycho Brahen tarkkoja havaintoja planeettojen asemista. Ensimmäinen ja toinen laki julkaistiin teoksessa Astronomia Nova (1609) ja kolmas laki teoksessa Harmonices Mundi (1619). Keplerin lait olivat tärkeä askel kohti Newtonin gravitaatioteoriaa: Isaac Newton osoitti myöhemmin, että Keplerin lait seuraavat vetovoimalaista 1/r^2 -vuorovaikutuksesta ja liikelakeista.
Rajoitukset ja nykyaikainen näkökulma
- Keplerin lait pätevät tarkasti ideaalissa kahden kappaleen tapauksessa, jossa keskuskappaleen massa on paljon suurempi kuin kiertäjän massa. Todellisissa systeemissä muiden kappaleiden vetovoimat aiheuttavat pieniä poikkeamia (perturbaatioita).
- Relativistiset ilmiöt (yleisen suhteellisuusteorian ennustukset) aiheuttavat pieniä korjauksia, jotka ovat havaittavissa esimerkiksi Maan radan läheisyydessä olevan Merkuriuksen perihelin esipreemiossa.
Sovellukset
Keplerin lakeja käytetään laajasti astronomiassa ja avaruustekniikassa: planeettojen ja satelliittien ratojen ennustamiseen, avaruusalusten lento- ja siirtoorbitien suunnitteluun, eksoplaneettojen massan ja radan arviointiin sekä koulutuksessa perusperiaatteiden havainnollistamiseen.
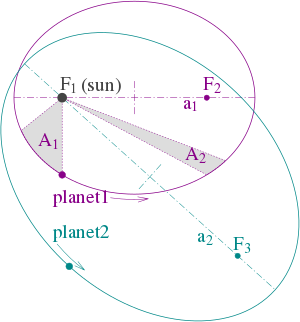
Kuva 1: Keplerin kolmen lain havainnollistaminen kahden planeetan radan avulla. (1) Kiertoradat ovat ellipsejä, joiden polttopisteet ovat ƒ1 ja ƒ2 ensimmäisen planeetan osalta ja ƒ1 ja ƒ3 toisen planeetan osalta. Aurinko sijaitsee polttopisteessä ƒ . 1 (2) Kahdella varjostetulla sektorilla A1 ja A2 on sama pinta-ala, ja planeetan 1 aika kattaa segmentti A1 on yhtä pitkä kuin aika kattaa segmentti A2 . (3) Planeetan 1 ja planeetan 2 kokonaiskiertoaikojen suhde on a13/2 : a23/2 .
Vertailu Kopernikukseen
Keplerin lait parantavat Kopernikuksen mallia. Jos planeettojen kiertoratojen eksentrisyydet otetaan nollaksi, Kepler on periaatteessa samaa mieltä Kopernikuksen kanssa:
- Planeetan kiertorata on ympyrä
- Aurinko kiertoradan keskipisteessä
- Planeetan nopeus kiertoradalla on vakio.
Kopernikuksen ja Keplerin tuntemien planeettojen kiertoratojen eksentrisyydet ovat pieniä, joten edellä esitetyt säännöt antavat hyvät likiarvot planeettojen liikkeelle; mutta Keplerin lait sopivat havaintoihin paremmin kuin Kopernikuksen lait.
Keplerin korjaukset eivät ole lainkaan ilmeisiä:
- Planeetan rata ei ole ympyrä vaan ellipsi.
- Aurinko ei ole keskipisteessä vaan elliptisen radan polttopisteessä.
- Planeetan lineaarinen nopeus tai kulmanopeus kiertoradalla ei ole vakio, mutta alueen nopeus on vakio.
Maapallon kiertoradan eksentrisyyden vuoksi aika maaliskuun päiväntasauksesta syyskuun päiväntasaukseen, noin 186 päivää, on eri aika kuin aika syyskuun päiväntasauksesta maaliskuun päiväntasaukseen, noin 179 päivää. Läpimitta leikkaisi radan yhtä suuriin osiin, mutta Maan päiväntasaajan suuntainen Auringon kautta kulkeva taso leikkaa radan kahteen osaan, joiden pinta-alat ovat suhteessa 186-179, joten Maan kiertoradan eksentrisyys on noin
ε ≈ π 4 186 - 179 186 + 179 ≈ 0.015 , {\displaystyle \varepsilon \approx {\frac {\pi }{4}}{\frac {186-179}{186+179}}\approx 0.015,} 
joka on lähellä oikeaa arvoa (0,016710219) (katso Maan kiertorata). Laskelma on oikea, kun periheli, jolloin Maa on lähimpänä Aurinkoa, osuu aurinkojaksolle. Nykyinen periheli, joka on lähellä tammikuun 4. päivää, on melko lähellä joulukuun 21. päivänseisausta.
Etsiä