Logaritminen asteikko: mitä se on ja mihin sitä käytetään

Logaritminen asteikko on asteikko, jota käytetään silloin, kun suureiden vaihteluväli on suuri. Yleisiä käyttökohteita ovat maanjäristyksen voimakkuus, äänen voimakkuus, valon voimakkuus ja liuosten pH. Logaritmisella asteikolla suuriin erotuksiin suhtaudutaan suhteellisina (kertolukuna) eikä absoluuttisina erotuksina, mikä tekee siitä sopivan tilanteisiin, joissa tiedot kattavat monta kertaluokkaa.

Mitä logaritminen asteikko tarkoittaa käytännössä?

Perusajatus on yksinkertainen: akselin paikan tai asteikon merkin arvo on verrannollinen suureen logaritmiin. Toisin sanoen kaksi yhtä suurta etäisyyttä asteikolla vastaavat samaa kertosuhdetta alkuperäisessä suureessa. Esimerkiksi kymmenkantainen (base 10) log-asteikko näyttää luvut 1, 10, 100, 1000 jne. yhtä suurin välein. Tämä tekee mahdolliseksi esittää sekä hyvin pieniä että hyvin suuria arvoja samassa kuvaajassa ilman, että pienet arvot jäävät näkymättömiin.

Matemaattinen muotoilu

Yksinkertaisimmillaan logaritminen asteikko ilmaistaan kaavoilla

koordinaatti = log_b(arvo),
tai käänteisesti arvo = b^(koordinaatti),

missä b on logaritmin kantaluku (yleisimmin 10, e tai 2). Esimerkkejä käytännöstä:

pH = −log10[H+] (eli pH kasvaa, kun vetysubstraatin konsentraatio pienenee).
desibeli (teho): dB = 10 · log10(P / P0); amplitudiperusteiset voimakkuudet (esim. jännite tai paine) usein ilmaistaan 20 · log10(A / A0).
Richterin tyyppiset maanjäristysasteikot perustuvat logaritmeihin: yhden yksikön nousu vastaa noin 10-kertaista amplitudia (ja energiassa suurta, likimain 31,6‑kertaista muutosta).

Esimerkkejä ja käytännön sovelluksia

Maanjäristykset: Richter-asteikko ja muut seismiset skaalajärjestelmät ilmaisevat heilurin amplitudin tai vapautuvan energian logaritmisesti, jotta pienet ja suuret tärinät saadaan vertailukelpoisiksi.
Ääni ja desibelit: Ihmisen kuulo reagoi suunnilleen suhteellisiin muutoksiin, joten äänenvoimakkuutta mitataan desibeleinä (katso äänen voimakkuus).
Valon voimakkuus ja astronomia: Tähtitieteessä kirkkaudet (magnitudit) ja valon intensiteetit käsitellään logaritmisesti, jotta erittäin kirkkaat ja hyvin himmeät kohteet saadaan esitettyä samassa järjestelmässä.
pH ja kemia: Happamuusasteikko pH on negatiivinen kymmenkantainen logaritmi vetysubstanssikonentraatiosta.
Äänentoisto ja käyttöliittymät: Logaritmisia asteikkoja käytetään myös liukusäätimissä, koska se helpottaa lukujen kertomista tai jakamista lisäämällä tai vähentämällä asteikolla olevia pituuksia ja vastaa paremmin ihmisen aisteja.

Miksi logaritmista asteikkoa kannattaa käyttää?

Se tiivistää laajat arvoalueet siten, että sekä pienet että suuret arvot näkyvät järkevästi.
Se muuntaa moninkertaiset erot yhtä suuriksi etäisyyksiksi — esimerkiksi kahden desimaalisarjan erot ilmaistaan samanlaisina etäisyyksinä, jos niiden suhde on sama.
Kun alkuperäiset ilmiöt ovat multiplicatiivisia tai noudattavat potenssilakia, logaritminen asteikko tekee mallinnuksesta ja tulkinnasta yksinkertaisempaa.
Jotkin aistimme toimivat logaritmisesti (todellisen tulovoiman kertominen lisää vakion havaittuun signaalin voimakkuuteen, ks. esim: Stevensin potenssilaki), joten log-asteikko vastaa havaintotapojamme erityisen hyvin. Erityisesti kuuloaistimme havaitsee taajuuksien yhtä suuret kertaluvut yhtä suurina äänenkorkeuseroina.

Rajoitukset ja varoitukset

Logaritmi ei ole määritelty nollalle tai negatiivisille arvoille, joten nollan tai negatiivisten mittausten käsittely vaatii muunnoksen tai siirron (esim. lisätään vakio ennen logaritmointia).
Keskiarvon laskeminen log-asteikolla ja alkuperäisessä asteikossa antaa eri tuloksia — log-asteikolla sopivampi keskiluku on geometrinen keskiarvo.
Logaritmisen skaalaan tottumattomalle lukijalle tulkinta voi aluksi tuntua epäintuitiiviselta: yhtä suuri etäisyys ei tarkoita samaa absoluuttista eroa, vaan samaa suhdetta.

Kuinka tulkita log-asteikon merkintöjä

Kun näet log-asteikon, katso, mikä on kantaluku (esim. 10, 2 tai e). Jos akselilla on merkitty 1, 10, 100, niin kyseessä on base‑10-asteikko: etäisyys 1 → 10 on sama kuin 10 → 100 (molemmat kertaluokan eli faktorilla 10). Jos mittausarvojen logaritmi on negatiivinen, se tarkoittaa, että alkuperäinen arvo on alle 1 (esim. log10(0,01) = −2).

Yhteenveto

Logaritminen asteikko on tehokas työkalu, kun käsitellään suureita, jotka vaihtelevat monia kertaluokkia. Se soveltuu hyvin luonnonilmiöihin ja mittauksiin, joissa suhteelliset muutokset ovat merkityksellisempiä kuin absoluuttiset erot. Samalla on tärkeää ymmärtää sen rajoitukset — erityisesti nollan ja negatiivisten arvojen käsittely sekä log- ja lineaaristen tulkintatapojen erot.

Useimmilla logaritmisilla asteikoilla logaritmisen mitan pieniä (mahdollisesti negatiivisia) arvoja vastaavat taustalla olevan suureen pienet kertoimet (tai suhteet).

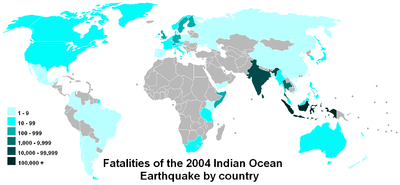
Log-asteikon avulla on helppo vertailla arvoja, jotka kattavat suuren vaihteluvälin, kuten tässä kartassa.

Liukusäätimen kaksi logaritmista asteikkoa

Esimerkkejä

Tunnettuja esimerkkejä tällaisista asteikoista ovat:

Richterin magnitudiasteikko ja momentin magnitudiasteikko (MMS) maanjäristysten voimakkuutta ja maan liikettä varten.
bel ja desibeli ja neper akustiselle teholle (äänekkyydelle) ja sähköteholle;
f-stoppien laskeminen valokuvauksen valotussuhteisiin;
luokitellaan alhaiset todennäköisyydet sen mukaan, kuinka monta "ysiä" on niiden toteutumattomuuden todennäköisyyden desimaalilaajennuksessa: esimerkiksi järjestelmä, joka epäonnistuu todennäköisyydellä 10⁻⁵on 99,999-prosenttisen luotettava: "viisi ysiä".
Entropia termodynamiikassa.
Informaatio informaatioteoriassa.
Maaperän hiukkaskokojakauman käyrät

Jotkin logaritmiset asteikot on suunniteltu siten, että logaritmisen mitan pieniä arvoja vastaavat suureet (tai suhdeluvut). Esimerkkejä tällaisista asteikoista ovat:

pH tarkoittaa happamuutta;
tähtien kirkkautta kuvaava tähtimittakaava;

Logaritminen asteikko on myös graafinen asteikko, joka on kuvaajan toisella tai molemmilla puolilla ja jossa luku x on painettu etäisyydelle c-log(x) pisteestä, joka on merkitty numerolla 1. Liukusäätimessä on logaritmiset asteikot, ja nomogrammeissa käytetään usein logaritmisia asteikkoja. Logaritmisella asteikolla yhtä suuri suuruusluokkaero esitetään yhtä pitkällä etäisyydellä. Kahden luvun geometrinen keskiarvo on lukujen puolivälissä.

Logaritminen kuvaajapaperi oli ennen tietokonegrafiikan tuloa tieteellinen perustyökalu. Yhden logaritmin asteikolla varustetulle paperille tehdyt kuvaajat voivat esittää eksponentiaaliset lait ja log-logaritmipaperilla potenssilait suorina viivoina (ks. semiloggigraafi, log-loggigraafi).

Kysymyksiä ja vastauksia

K: Mikä on logaritminen asteikko?

A: Logaritminen asteikko on asteikko, jota käytetään, kun suureiden vaihteluväli on suuri.

K: Mitkä ovat esimerkkejä asioista, joita voidaan mitata logaritmisella asteikolla?

V: Maanjäristyksen voimakkuutta, äänen voimakkuutta, valon voimakkuutta, epidemioiden leviämisnopeutta ja liuosten pH:ta voidaan mitata logaritmisella asteikolla.

K: Miten logaritminen asteikko eroaa tavallisesta lineaarisesta asteikosta?

V: Logaritminen asteikko perustuu suuruusluokkiin eikä tavalliseen lineaariseen asteikkoon. Asteikon kunkin merkin arvo on edellisen merkin arvo kerrottuna vakiolla.

K: Mitä hyötyä logaritmisen asteikon käytöstä on?

V: Logaritminen asteikko voi pienentää suuren arvoalueen helpommin hallittavaksi, mikä voi olla hyödyllistä käsiteltäessä tietoja, jotka kattavat laajan arvoalueen.

K: Mikä on Stevensin potenssilaki ja miten se liittyy logaritmisiin asteikkoihin?

V: Stevensin potenssilaki kuvaa sitä, miten jotkin aistimme toimivat logaritmisesti, jolloin todellisen tulovoiman kertominen lisää vakion havaittuun signaalin voimakkuuteen. Tämän vuoksi logaritmiset asteikot ovat erityisen sopivia näille tulomäärille.

K: Miksi logaritminen asteikko on erityisen hyödyllinen äänen voimakkuuden mittaamisessa?

V: Kuuloaistimme havaitsee taajuuksien yhtä suuret kertaluvut yhtä suurina äänenkorkeuseroina, joten logaritminen asteikko voi esittää tarkasti tämän äänen taajuuden ja koetun äänenvoimakkuuden välisen suhteen.

Kysymys: Mikä on taustalla olevan suureen pienten kertalukujen ja useimpien logaritmisissa asteikoissa käytetyn logaritmisen mitan välinen suhde?

V: Useimmilla logaritmisilla asteikoilla taustalla olevan suureen pienet kertoimet (tai suhteet) vastaavat pieniä (mahdollisesti negatiivisia) logaritmisen mitan arvoja.